6174: ਇੱਕ ਰਹੱਸਮਈ ਸੰਖਿਆ ਜੋ ਦਹਾਕਿਆਂ ਤੋਂ ਗਣਿਤ ਦੇ ਮਾਹਰਾਂ ਲਈ ਬਣੀ ਹੋਈ ਹੈ ਇੱਕ ਪਹੇਲੀ

- ਲੇਖਕ, ਡੇਲੀਆ ਵੈਂਚੁਰਾ
- ਰੋਲ, ਬੀਬੀਸੀ ਪੱਤਰਕਾਰ
- ਪੜ੍ਹਨ ਦਾ ਸਮਾਂ: 7 ਮਿੰਟ
ਨੰਬਰ 6174 ਨੂੰ ਧਿਆਨ ਨਾਲ ਦੇਖੋ
ਪਹਿਲੀ ਨਜ਼ਰ 'ਚ ਇਹ ਕੁਝ ਖ਼ਾਸ ਨਹੀਂ ਲੱਗਦਾ ਪਰ ਸਾਲ 1949 ਤੋਂ ਇਹ ਗਣਿਤ ਦੇ ਮਾਹਰਾਂ ਲਈ ਇੱਕ ਪਹੇਲੀ ਬਣਿਆ ਹੋਇਆ ਹੈI
ਇਸ ਦੀ ਵਜ੍ਹਾ ਕੀ ਹੈ? ਇਹ ਸਮਝਣ ਲਈ ਇਨ੍ਹਾਂ ਕੁੱਝ ਦਿਲਚਸਪ ਤੱਥਾਂ ਨੂੰ ਦੇਖੋ:
ਕੋਈ ਵੀ ਚਾਰ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ ਆਪਣੇ ਮਨ ਮੁਤਾਬਕ ਚੁਣੋ, ਪਰ ਕੋਈ ਵੀ ਅੰਕ ਦੁਬਾਰਾ ਨਹੀਂ ਆਉਣਾ ਚਾਹੀਦਾ, ਉਦਾਹਰਨ ਵਜੋਂ 1234
ਇਨ੍ਹਾਂ ਨੂੰ ਘੱਟਦੇ ਕ੍ਰਮ ਵਿੱਚ ਲਿਖੋ: 4321
ਹੁਣ ਇਨ੍ਹਾਂ ਨੂੰ ਵੱਧਦੇ ਕ੍ਰਮ ਵਿੱਚ ਲਿਖੋ: 1234
ਹੁਣ ਵੱਡੀ ਸੰਖਿਆ ਵਿੱਚੋਂ ਛੋਟੀ ਸੰਖਿਆ ਘਟਾ ਦਿਓ: 4321 - 1234
ਹੁਣ ਜੋ ਨਤੀਜਾ ਨਿਕਲਿਆ ਉਸ ਦੇ ਨਾਲ 2, 3 ਅਤੇ 4 ਅੰਕਾਂ ਨੂੰ ਦੁਹਰਾਓI
ਆਓ ਇਸ ਨੂੰ ਕਰਕੇ ਦੇਖਦੇ ਹਾਂ
4321 - 1234 = 3087
ਇਨ੍ਹਾਂ ਅੰਕਾਂ ਨੂੰ ਘੱਟਦੇ ਕ੍ਰਮ ਵਿੱਚ ਰੱਖੋ: 8730
ਹੁਣ ਇਨ੍ਹਾਂ ਨੂੰ ਵੱਧਦੇ ਕ੍ਰਮ ਵਿੱਚ ਰੱਖੋ: 0378
ਹੁਣ ਵੱਡੀ ਸੰਖਿਆ ਵਿੱਚੋਂ ਛੋਟੀ ਸੰਖਿਆ ਨੂੰ ਘਟਾ ਦਿਓ: 8730 - 0378 = 8352
ਨਤੀਜੇ 'ਚ ਮਿਲੀ ਸੰਖਿਆ ਨਾਲ ਉਪਰੋਕਤ 3 ਪ੍ਰਕਿਰਿਆਵਾਂ ਨੂੰ ਦੁਹਰਾਓ
ਹੁਣ ਸੰਖਿਆ 8352 ਨਾਲ ਅਜਿਹਾ ਹੀ ਕਰਕੇ ਦੇਖਦੇ ਹਾਂ
ਹੁਣ ਸੰਖਿਆ 8352 ਨਾਲ ਇਹੀ ਕਰਕੇ ਦੇਖਦੇ ਹਾਂ

ਤਸਵੀਰ ਸਰੋਤ, Getty Images
8532 - 2358 = 6174
6174 ਨਾਲ ਇਹ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਦੁਹਰਾਉਂਦੇ ਹਾਂ, ਯਾਨੀ ਅੰਕਾਂ ਨੂੰ ਵੱਧਦੇ ਅਤੇ ਘੱਟਦੇ ਕ੍ਰਮ ਵਿੱਚ ਰੱਖਣ ਤੋਂ ਬਾਅਦ ਘਟਾਉਂਦੇ ਹਾਂI
7641 - 1467 = 6174
ਜਿਵੇਂ ਕਿ ਤੁਸੀਂ ਦੇਖ ਸਕਦੇ ਹੋ, ਇਸ ਤੋਂ ਬਾਅਦ ਮੁੜ ਇਹ ਪ੍ਰਕਿਰਿਆ ਦੁਹਰਾਉਣ ਦਾ ਕੋਈ ਮਤਲਬ ਨਹੀਂ ਰਹਿੰਦਾ ਕਿਉਂਕਿ ਨਤੀਜਾ ਫਿਰ ਵੀ ਓਹੀ ਮਿਲੇਗਾ: 6174
ਪਰ ਹੋ ਸਕਦਾ ਹੈ ਕਿ ਤੁਸੀਂ ਸੋਚੋ ਕਿ ਇਹ ਸਿਰਫ਼ ਇੱਕ ਇਤਫ਼ਾਕ ਹੈ ਤਾਂ ਆਓ ਕਿਸੇ ਹੋਰ ਨੰਬਰ ਨਾਲ ਇਹੀ ਪ੍ਰਕਿਰਿਆ ਦੁਹਰਾਉਂਦੇ ਹਾਂI ਉਦਾਹਰਨ ਵਜੋਂ 2005 ਲੈਂਦੇ ਹਾਂI
5200 - 0025 = 5175
7551 - 1557 = 5994
9954 - 4599 = 5355
5553 - 3555 = 1998
9981 - 1899 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174
ਤੁਸੀਂ ਆਪ ਦੇਖ ਸਕਦੇ ਹੋ, ਭਾਵੇਂ ਕੋਈ ਵੀ ਚਾਰ ਅੰਕ ਚੁਣੋ- ਅੰਤਿਮ ਨਤੀਜਾ 6174 ਹੀ ਮਿਲਦਾ ਹੈ ਅਤੇ ਇਸ ਤੋਂ ਬਾਅਦ ਇਹ ਪ੍ਰਕਿਰਿਆ ਦੁਹਰਾਉਣ ਨਾਲ ਓਹੀ ਨਤੀਜਾ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈI
ਭਾਰਤੀ ਗਣਿਤ ਮਾਹਰ ਦੁਆਰਾ ਕੀਤੀ ਗਈ ਖੋਜ

ਤਸਵੀਰ ਸਰੋਤ, Getty Images
ਭਾਰਤੀ ਗਣਿਤ ਦੇ ਮਾਹਰ ਦੱਤਾਤ੍ਰੇਯ ਰਾਮਚੰਦਰ ਕਾਪ੍ਰੇਕਰ (1905-1986) ਨੂੰ ਅੰਕਾਂ ਨਾਲ ਪ੍ਰਯੋਗ ਕਰਨਾ ਬਹੁਤ ਪਸੰਦ ਸੀI ਇਸ ਪ੍ਰਕਿਰਿਆ ਦੌਰਾਨ ਉਨ੍ਹਾਂ ਦਾ ਮੇਲ ਇਸ ਰਹੱਸਮਈ ਸੰਖਿਆ 6174 ਨਾਲ ਹੋਇਆI
ਸਾਲ 1949 'ਚ ਮਦਰਾਸ ਵਿੱਚ ਹੋਏ ਇੱਕ ਗਣਿਤ ਸੰਮੇਲਨ ਦੌਰਾਨ ਕਾਪ੍ਰੇਕਰ ਨੇ ਦੁਨੀਆ ਨੂੰ ਇਸ ਸੰਖਿਆ ਨਾਲ ਜਾਣੂ ਕਰਵਾਇਆI
ਉਹ ਕਹਿੰਦੇ ਸਨ, "ਜਿਸ ਤਰ੍ਹਾਂ ਨਸ਼ੇ 'ਚ ਰਹਿਣ ਲਈ ਸ਼ਰਾਬੀ ਸ਼ਰਾਬ ਪੀਂਦਾ ਹੈI ਸੰਖਿਆਵਾਂ ਦੇ ਮਾਮਲੇ 'ਚ ਮੇਰੇ ਨਾਲ ਵੀ ਬਿਲਕੁਲ ਅਜਿਹਾ ਹੀ ਹੈI"
ਉਹ ਮੁੰਬਈ ਯੂਨੀਵਰਸਿਟੀ ਤੋਂ ਪੜ੍ਹੇ ਹੋਏ ਸਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੇ ਮਹਾਰਾਸ਼ਟਰ ਦੇ ਦੇਵਲਾਲੀ ਕਸਬੇ ਵਿੱਚ ਇੱਕ ਸਕੂਲ 'ਚ ਪੜ੍ਹਾਉਂਦੇ ਆਪਣੀ ਜ਼ਿੰਦਗੀ ਬਤੀਤ ਕੀਤੀ ਸੀI
ਹਾਲਾਂਕਿ, ਉਨ੍ਹਾਂ ਦੀ ਖੋਜ ਦਾ ਮਜ਼ਾਕ ਬਣਾਇਆ ਗਿਆ ਅਤੇ ਭਾਰਤੀ ਗਣਿਤ ਮਾਹਰਾਂ ਨੇ ਇਸ ਨੂੰ ਖਾਰਜ ਕਰ ਦਿੱਤਾI ਪਰ ਅਕਸਰ ਉਨ੍ਹਾਂ ਨੂੰ ਸਕੂਲਾਂ ਅਤੇ ਕਾਲਜਾਂ ਵਿੱਚ ਆਪਣੇ ਵਿਲੱਖਣ ਤਰੀਕੇ ਬਾਰੇ ਗੱਲ ਕਰਨ ਲਈ ਬੁਲਾਇਆ ਜਾਂਦਾ ਸੀI
ਹੌਲ਼ੀ-ਹੌਲ਼ੀ ਉਨ੍ਹਾਂ ਦੀ ਖੋਜ ਨੂੰ ਲੈ ਕੇ ਭਾਰਤ ਅਤੇ ਵਿਦੇਸ਼ਾਂ ਵਿੱਚ ਚਰਚਾ ਹੋਣ ਲੱਗੀ ਅਤੇ 1970 ਦੇ ਦਹਾਕੇ ਤੱਕ ਅਮਰੀਕਾ ਦੇ ਸਭ ਤੋਂ ਵੱਧ ਵਿਕਣ ਵਾਲੇ ਅਤੇ ਗਣਿਤ 'ਚ ਦਿਲਚਸਪੀ ਰੱਖਣ ਵਾਲੇ ਲੇਖਕ ਮਾਰਟਿਨ ਗਾਰਡਰ ਨੇ ਇੱਕ ਮਸ਼ਹੂਰ ਵਿਗਿਆਨਿਕ ਮੈਗਜ਼ੀਨ 'ਸਾਇੰਟਿਫਿਕ ਅਮਰੀਕਾ' ਵਿੱਚ ਉਨ੍ਹਾਂ ਬਾਰੇ ਲਿਖਿਆI
ਅੱਜ ਕਾਪ੍ਰੇਕਰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਖੋਜ ਨੂੰ ਮਾਨਤਾ ਮਿਲ ਰਹੀ ਹੈ ਅਤੇ ਇਸ 'ਤੇ ਦੁਨੀਆ ਭਰ ਦੇ ਗਣਿਤ ਮਾਹਰ ਕੰਮ ਕਰ ਰਹੇ ਹਨ।
ਓਸਾਕਾ ਯੂਨੀਵਰਸਿਟੀ ਵਿੱਚ ਅਰਥਸ਼ਾਸਤਰ ਦੇ ਪ੍ਰੋਫੈਸਰ ਯੂਤਾਕਾ ਨਿਸ਼ੀਯਾਮਾ ਦਾ ਕਹਿਣਾ ਹੈ, "ਸੰਖਿਆ 6174 ਅਸਲੀਅਤ 'ਚ ਰਹੱਸਾਂ ਨਾਲ ਭਰੀ ਹੋਈ ਹੈ।"
ਇੱਕ ਆਨਲਾਈਨ ਮੈਗਜ਼ੀਨ +ਪਲਸ ਵਿੱਚ ਨਿਸ਼ੀਯਾਮਾ ਨੇ ਲਿਖਿਆ ਕਿ ਕਿਵੇਂ ਉਨ੍ਹਾਂ ਨੇ ਕੰਪਿਊਟਰ ਦੀ ਮਦਦ ਨਾਲ ਸਾਰੀਆਂ ਚਾਰ ਅੰਕਾਂ ਵਾਲੀਆਂ ਸੰਖਿਆਵਾਂ 'ਤੇ ਪ੍ਰਯੋਗ ਕਰਕੇ ਸੰਖਿਆ 6174 ਤੱਕ ਪਹੁੰਚਣ ਦੀ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਸਮਝਿਆ।
ਉਨ੍ਹਾਂ ਦਾ ਨਤੀਜਾ ਇਹ ਸੀ ਕਿ ਹਰ ਉਹ ਚਾਰ ਅੰਕਾਂ ਵਾਲੀ ਸੰਖਿਆ, ਜਿਸ ਦੇ ਸਾਰੇ ਅੰਕ ਆਪਸ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਹੋਣ, ਕਾਪ੍ਰੇਕਰ ਦੀ ਪ੍ਰਕਿਰਿਆ ਅਧੀਨ ਸੱਤ ਕਦਮਾਂ ਵਿੱਚ ਸੰਖਿਆ 6174 ਤੱਕ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ।
ਨਿਸ਼ੀਯਾਮਾ ਅਨੁਸਾਰ, "ਜੇਕਰ ਤੁਸੀਂ ਕਾਪ੍ਰੇਕਰ ਦੀ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਸੱਤ ਵਾਰ ਦੁਹਰਾਉਣ ਤੋਂ ਬਾਅਦ ਵੀ 6174 ਤੱਕ ਨਹੀਂ ਪਹੁੰਚਦੇ ਤਾਂ ਇਸ ਦਾ ਮਤਲਬ ਹੈ ਕਿ ਤੁਸੀਂ ਕਿਤੇ ਨਾ ਕਿਤੇ ਗਲਤੀ ਕੀਤੀ ਹੈ ਅਤੇ ਤੁਹਾਨੂੰ ਦੁਬਾਰਾ ਕੋਸ਼ਿਸ਼ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ।"
ਕਿਵੇਂ ਬਣਿਆ ਜਾਦੂਈ ਨੰਬਰ?
ਇਸ ਤਰ੍ਹਾਂ ਦੀਆਂ ਕਈ ਖ਼ਾਸ ਸੰਖਿਆਵਾਂ ਹੁੰਦੀਆਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਦੀ ਸਹੀ ਗਿਣਤੀ ਦਾ ਅੰਦਾਜ਼ਾ ਨਹੀਂ ਹੈ।
ਪਰ ਇਹ ਤਾਂ ਜ਼ਰੂਰ ਹੈ ਕਿ ਕਾਪ੍ਰੇਕਰ ਕਾਂਸਟੈਂਟ ਵਾਂਗ ਹੀ ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੀਆਂ ਸੰਖਿਆਵਾਂ ਲਈ ਵੀ ਇੱਕ ਅਜਿਹਾ ਹੀ ਤਰੀਕਾ ਮੌਜੂਦ ਹੈ।
ਮੰਨ ਲਓ, ਅਸੀਂ ਇੱਕ ਸੰਖਿਆ ਚੁਣੀ 574, ਆਓ ਇਸ ਨਾਲ ਵੀ ਉਹੀ ਪ੍ਰਕਿਰਿਆ ਦੁਹਰਾਈਏ।
754 - 457 = 297
972 - 279 = 693
963 - 369 = 594
954 - 459 = 495
954 - 459 = 495
ਇਸ ਤਰ੍ਹਾਂ ਤੁਹਾਨੂੰ ਇੱਕ ਹੋਰ ਜਾਦੂਈ ਨੰਬਰ 495 ਮਿਲਦਾ ਹੈI
ਗਣਿਤ ਮਾਹਰਾਂ ਦਾ ਕਹਿਣਾ ਹੈ ਕਿ ਇਹ ਕਾਂਸਟੈਂਟ (ਸਥਿਰ ਅੰਕ) ਸਿਰਫ਼ ਤਿੰਨ ਅਤੇ ਚਾਰ ਅੰਕਾਂ ਵਾਲੀਆਂ ਸੰਖਿਆਵਾਂ ਨਾਲ ਹੀ ਮਿਲਦੀਆਂ ਹਨI
ਟੈਕਨੀਕਲਰ ਵਿੱਚ 6174 ਦੀ ਵਰਤੋਂ

ਤਸਵੀਰ ਸਰੋਤ, Getty Images
ਮੁੰਬਈ ਦੀ ਸੀਗ੍ਰਾਮ ਟੈਕਨਾਲੋਜੀਜ਼ ਫਾਊਂਡੇਸ਼ਨ ਨੇ ਪਿੰਡਾਂ ਅਤੇ ਆਦਿਵਾਸੀ ਸਕੂਲਾਂ ਲਈ ਇੱਕ ਆਈਟੀ ਲਰਨਿੰਗ ਪਲੇਟਫਾਰਮ ਵਿਕਸਿਤ ਕੀਤਾ ਹੈ।
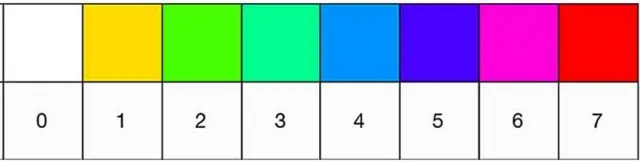
ਇਸ ਪਲੇਟਫਾਰਮ ਨੇ 6174 ਸੰਖਿਆ ਨੂੰ ਆਪਣੇ ਵਿਸ਼ੇ ਦਾ ਹਿੱਸਾ ਬਣਾਇਆ ਹੈ ਅਤੇ ਇਸ ਦੇ ਅੰਕਾਂ ਨੂੰ ਰੰਗਾਂ ਦੇ ਨਾਲ ਦਰਸਾਉਣ ਦਾ ਫ਼ੈਸਲਾ ਕੀਤਾ ਹੈ।
ਫਾਊਂਡੇਸ਼ਨ ਦੇ ਸੰਸਥਾਪਕ ਗਿਰੀਸ਼ ਆਰਾਬੇਲ ਨੇ ਬੀਬੀਸੀ ਨੂੰ ਦੱਸਿਆ ਕਿ ਉਹ ਬੱਚਿਆਂ ਵਿੱਚ ਗਣਿਤ ਪ੍ਰਤੀ ਦਿਲਚਸਪੀ ਪੈਦਾ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰ ਰਹੇ ਹਨ।
ਉਹ ਕਹਿੰਦੇ ਹਨ, "ਕਾਪ੍ਰੇਕਰ ਕਾਂਸਟੈਂਟ ਇੰਨਾ ਦਿਲਚਸਪ ਹੈ ਕਿ ਜਦੋਂ ਤੁਸੀਂ ਉਸ ਦੇ ਦੱਸੇ ਤਰੀਕੇ ਅਪਣਾਉਂਦੇ ਹੋ ਤਾਂ ਅਖ਼ੀਰ ਵਿੱਚ ਉਹ ਤੁਹਾਨੂੰ ਉਸ ਪਲ ਤੱਕ ਲੈ ਜਾਂਦਾ ਹੈ ਜਿੱਥੇ ਖੁਸ਼ੀ ਦਾ ਕੋਈ ਠਿਕਾਣਾ ਨਹੀਂ ਰਹਿੰਦਾ। ਇਹ ਉਹ ਅਨੁਭਵ ਹੈ ਜੋ ਰਵਾਇਤੀ ਗਣਿਤ ਦੇ ਪਾਠਕ੍ਰਮ ਨੂੰ ਸਿੱਖਦੇ ਹੋਏ ਨਹੀਂ ਮਿਲ ਸਕਦਾ।"
ਆਰਾਬੇਲ ਦੀ ਟੀਮ ਨੇ 6174 ਤੱਕ ਪਹੁੰਚਣ ਲਈ ਲੱਗਣ ਵਾਲੇ ਸਾਰੇ ਕਦਮਾਂ ਨੂੰ ਕਲਰ ਕੋਡ ਦੇ ਰੂਪ ਵਿੱਚ ਦਰਸਾਉਣ ਦਾ ਫੈਸਲਾ ਕੀਤਾ। ਉਹ ਜਾਣਦੇ ਸਨ ਕਿ ਇਸ ਜਾਦੂਈ ਨੰਬਰ ਤੱਕ ਪਹੁੰਚਣ ਲਈ ਸੱਤ ਤੋਂ ਵੱਧ ਕਦਮ ਨਹੀਂ ਲੱਗਦੇ।
ਇਹ ਉਸ ਕੋਡ ਦਾ ਆਧਾਰ ਬਣਿਆ, ਜਿਸ ਨੂੰ ਰੈਸਪਬੈਰੀ ਪਾਈ 'ਤੇ ਦੁਬਾਰਾ ਤਿਆਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਦਰਅਸਲ ਇਹ ਇੱਕ ਸਸਤਾ ਅਤੇ ਕਰੈਡਿਟ ਕਾਰਡ ਦੇ ਆਕਾਰ ਦਾ ਕੰਪਿਊਟਰ ਹੁੰਦਾ ਹੈI ਇਹ ਆਮ ਤੌਰ 'ਤੇ ਸਾਇੰਸ, ਤਕਨਾਲੋਜੀ, ਇੰਜੀਨੀਅਰਿੰਗ ਅਤੇ ਗਣਿਤ ਦੀ ਪੜ੍ਹਾਈ ਵਿੱਚ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ।
ਇਸ ਤੋਂ ਬਾਅਦ ਵਿਦਿਆਰਥੀ ਵੋਲਫਰੇਮ ਲੈਂਗੁਏਜ (ਕੰਪਿਊਟਰ ਦੀ ਗਣਿਤੀ ਭਾਸ਼ਾ) ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਇਸ ਦੀ ਵਿਆਖਿਆ ਅਤੇ ਮੌਜੂਦਾ ਚਾਰ ਅੰਕਾਂ ਵਾਲੇ10,000 ਨੰਬਰ ਲਈ ਇਸ ਦਾ ਵਿਸ਼ਲੇਸ਼ਣ ਕਰ ਸਕਦੇ ਹਨ।
6174 ਤੱਕ ਪਹੁੰਚਣ ਲਈ ਇਹ ਕੰਪਿਊਟਰ ਲੈਂਗੁਏਜ ਇੱਕ ਪੈਟਰਨ ਤਿਆਰ ਕਰਦੀ ਹੈ ਅਤੇ ਇਸ ਨਾਲ ਬਹੁਰੰਗੀ ਗ੍ਰਿਡ ਬਣਦਾ ਹੈI
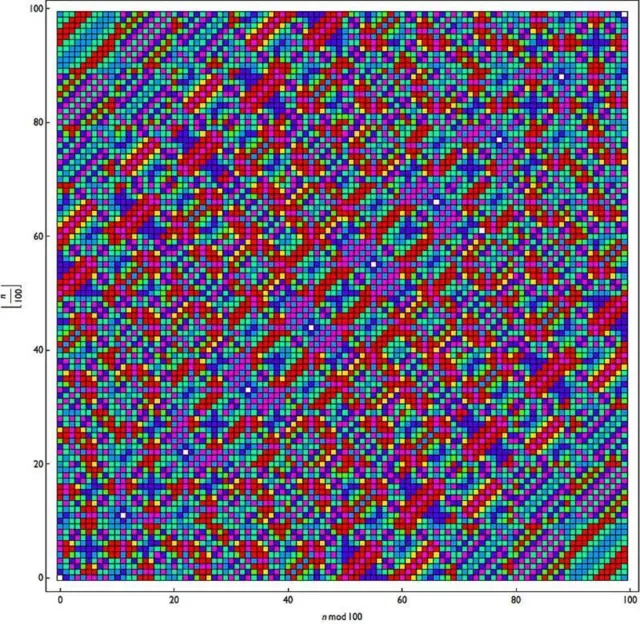
ਤਸਵੀਰ ਸਰੋਤ, Scigram Technologies Foundation
ਜੇਕਰ ਤੁਹਾਨੂੰ ਕੋਡਿੰਗ ਕਰਦਿਆਂ ਟਾਂਕ ਸੰਖਿਆਵਾਂ (ਔਡ ਨੰਬਰ) ਨੀਲੇ ਰੰਗ ਵਿੱਚ ਅਤੇ ਜਿਸਤ ਸੰਖਿਆਵਾਂ (ਈਵਨ ਨੰਬਰ) ਹਰੇ ਰੰਗ ਵਿੱਚ ਦਿੱਖਣ ਤਾਂ ਇਸ ਦਾ ਅਰਥ ਕੀ ਹੋਵੇਗਾ?
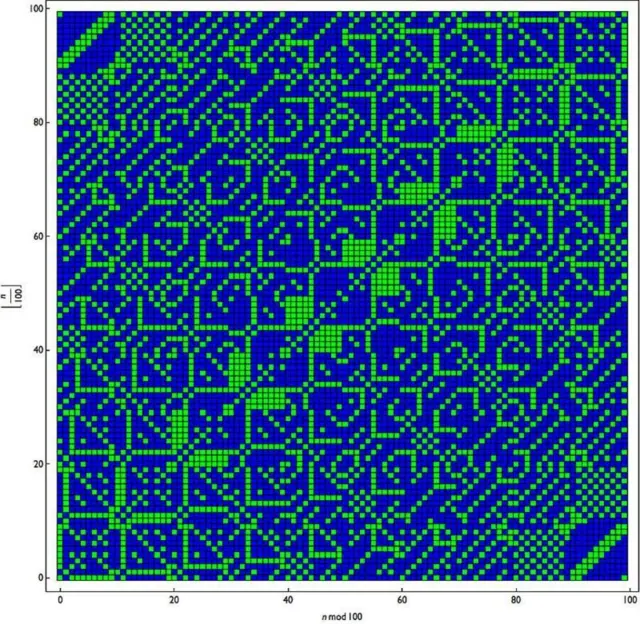
ਤਸਵੀਰ ਸਰੋਤ, Scigram Technologies Foundation
ਅਤੇ ਜੇਕਰ ਤੁਸੀਂ ਪ੍ਰਾਇਮ ਨੰਬਰਾਂ ਨੂੰ ਹਰੇ ਰੰਗ ਵਿੱਚ ਦਿਖਾਉਂਦੇ ਹੋ ਅਤੇ ਬਾਕੀ ਸਾਰੀਆਂ ਸੰਖਿਆਵਾਂ ਨੀਲੇ ਰੰਗ ਵਿੱਚ ਦਿਖਾਓ ਤਾਂ ਕੀ ਪੈਟਰਨ ਪੂਰੀ ਤਰ੍ਹਾਂ ਬਦਲ ਜਾਂਦਾ ਹੈ?
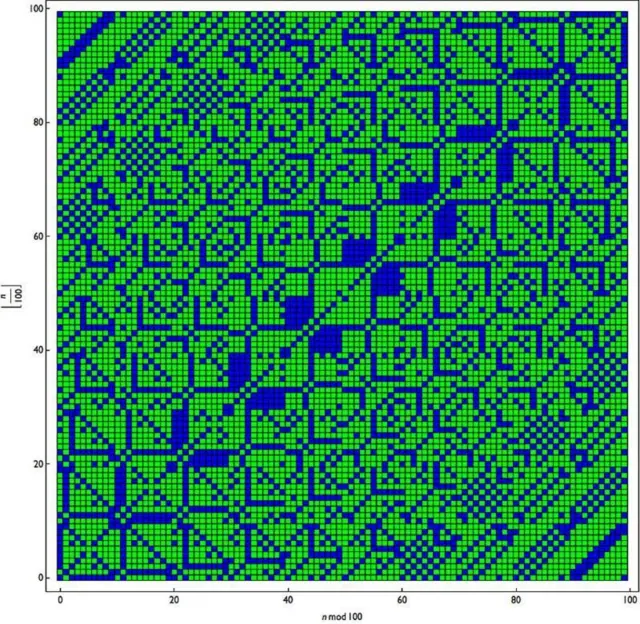
ਤਸਵੀਰ ਸਰੋਤ, Scigram Technologies Foundation
ਖੇਡ-ਖੇਡ ਵਿੱਚ ਗਣਿਤ ਸਿੱਖਣਾ

ਤਸਵੀਰ ਸਰੋਤ, Getty Images
ਕਾਪ੍ਰੇਕਰ ਕਾਂਸਟੈਂਟ ਦਾ ਸਿਰਫ਼ ਖੇਡ-ਖੇਡ ਵਿੱਚ ਗਣਿਤ ਸਿੱਖਣ ਦੇ ਤਰੀਕਿਆਂ ਵਿੱਚ ਹੀ ਯੋਗਦਾਨ ਨਹੀਂ ਹੈ।
ਤੁਸੀਂ ਕਾਪ੍ਰੇਕਰ ਨੰਬਰ ਬਾਰੇ ਵੀ ਜ਼ਰੂਰ ਸੁਣਿਆ ਹੋਵੇਗਾ। ਇਸ ਵਿੱਚ ਇੱਕ ਅਜਿਹੀ ਸੰਖਿਆ ਹੈ ਜਿਸ ਦਾ ਜੇਕਰ ਵਰਗ ਕੀਤਾ ਜਾਵੇ ਤਾਂ ਇਸ ਦੇ ਨਤੀਜੇ ਨੂੰ ਦੋ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਦਾ ਜੋੜ ਅਸਲ ਸੰਖਿਆ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ।
ਇਸ ਨੂੰ ਕੁਝ ਇਸ ਤਰ੍ਹਾਂ ਸਮਝ ਸਕਦੇ ਹਾਂ:
297² = 88,209
88 + 209 = 297