National Mathematics Day: ਭਾਰਤ ਨੂੰ ਇਸ ਲਈ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਗਣਿਤ ਦਾ ਵਿਸ਼ਵ ਗੁਰੂ
ਤਸਵੀਰ ਸਰੋਤ, Getty Images
ਚੀਨ ਵਾਂਗ ਹੀ ਭਾਰਤ ਨੇ ਗਣਿਤ ਵਿੱਚ ਇਸ਼ਾਰੀਆ ਜਾਂ ਡੈਸੀਮਲ ਸਿਸਟਮ ਦੀ ਵਰਤੋਂ ਬਹੁਤ ਪਹਿਲਾਂ ਹੀ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀ ਸੀ। ਮਾਹਿਰਾਂ ਮੁਤਾਬਕ ਇਸ ਦੇ ਪ੍ਰਮਾਣ ਤੀਜੀ ਸਦੀ ਤੋਂ ਮਿਲਦੇ ਹਨ।
ਇਹ ਅੱਜ ਵੀ ਵਰਤਿਆ ਜਾਣ ਵਾਲਾ ਇਕਾਈ-ਦਹਾਈ-ਸੈਂਕੜੇ ਵਾਲਾ ਹਿਸਾਬ ਹੈ।
ਇਹ ਤਾਂ ਨਹੀਂ ਪਤਾ ਕਿ ਇਹ ਸ਼ੁਰੂ ਕਿਵੇਂ ਕੀਤਾ ਗਿਆ ਪਰ ਇਸੇ ਨਾਲ ਗਣਿਤ ਦਾ ਆਧਾਰ ਮੰਨੀਆਂ ਜਾਣ ਵਾਲੀਆਂ ਸੰਖਿਆਵਾਂ — 1 ਤੋਂ 9 — ਦੁਨੀਆਂ ਭਰ ਵਿੱਚ ਵਰਤੀਆਂ ਜਾਣ ਲੱਗੀਆਂ।
ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਭਾਰਤ ਵਿੱਚ ਹੀ ਇੱਕ ਨਵੀਂ ਸੰਖਿਆ ਦਾ ਜਨਮ ਹੋਇਆ — ਸਿਫ਼ਰ ਭਾਵ ਜ਼ੀਰੋ। ਸਿਫ਼ਰ ਦੀ ਵਰਤੋਂ ਦੇ ਸਬੂਤ ਨੌਵੀਂ ਸਦੀ ਤੋਂ ਮਿਲਦੇ ਹਨ ਪਰ ਇਹ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਇਸ ਤੋਂ ਵੀ ਸੈਂਕੜੇ ਸਾਲ ਪਹਿਲਾਂ ਤੋਂ ਸਿਫ਼ਰ ਮੌਜੂਦ ਸੀ।
ਇਹ ਵੀ ਪੜ੍ਹੋ

ਤਸਵੀਰ ਸਰੋਤ, Getty Images
ਮੱਧ ਭਾਰਤ ਦੇ ਗਵਾਲੀਅਰ ਸ਼ਹਿਰ ਵਿੱਚ ਇੱਕ ਨਿੱਕੇ ਜਿਹੇ ਮੰਦਿਰ ’ਚ ਵੀ ਇਹ ਅਜੀਬ ਜਿਹੀ ਜਾਪਣ ਵਾਲੀ ਸੰਖਿਆ ਦਰਜ ਹੈ।
ਇਸ ਮੰਦਿਰ ਦੀ ਇਸੇ ਲਈ ਬਹੁਤ ਪ੍ਰਸਿੱਧੀ ਹੋਈ ਅਤੇ ਇੱਥੇ ਖਾਸ ਤੌਰ 'ਤੇ ਲੋਕ ਆਉਣ ਲੱਗੇ।
ਗੱਲ ਅਜੀਬ ਜ਼ਰੂਰ ਲੱਗੇਗੀ ਪਰ ਇਹ ਸੱਚ ਹੈ ਕਿ ਭਾਰਤ ਵੱਲੋਂ ਵਰਤੇ ਜਾਣ ਤੋਂ ਪਹਿਲਾਂ ਜ਼ੀਰੋ ਹੁੰਦਾ ਹੀ ਨਹੀਂ ਸੀ।
ਇਹ ਵੀ ਜ਼ਰੂਰ ਪੜ੍ਹੋ

ਪ੍ਰਾਚੀਨ ਮਿਸਰ, ਚੀਨ ਅਤੇ ਮੈਸੋਪੋਟਾਮੀਆ ਦੀ ਸੱਭਿਅਤਾਵਾਂ ਵਿੱਚ ਵੀ ਸਿਫ਼ਰ ਮੌਜੂਦ ਤਾਂ ਸੀ ਪਰ ਸਿਰਫ ਇੱਕ ਖਾਲੀ ਸਥਾਨ ਦੇ ਸੂਚਕ ਵਜੋਂ।
ਭਾਰਤੀ ਸੱਭਿਅਤਾ ਨੇ ਇਸ ਨੂੰ ਇੱਕ ਸੰਖਿਆ ਮੰਨ ਕੇ ਉਸ ਤਰ੍ਹਾਂ ਵਰਤਿਆ ਜਿਸ ਤਰ੍ਹਾਂ ਇਹ ਅੱਜ ਵੀ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ।
ਸਿਫ਼ਰ ਰਾਹੀਂ ਸੰਖਿਆ ਦਾ ਮੁੱਲ ਵਧਾਇਆ ਜਾਣ ਲੱਗਾ। ਇਸ ਨਾਲ ਗਣਿਤ ਵਿੱਚ ਇਨਕਲਾਬ ਜਿਹਾ ਹੀ ਆ ਗਿਆ।
ਇਸ ਤੋਂ ਬਾਅਦ ਹੀ ਵੱਡੀਆਂ ਸੰਖਿਆਵਾਂ ਲਿਖਣਾ ਸੰਭਵ ਹੋ ਸਕਿਆ।

ਤਸਵੀਰ ਸਰੋਤ, Getty Images
ਸਿਫ਼ਰ ਆਇਆ ਕਿੱਥੋਂ?
ਇਸ ਸਵਾਲ ਦਾ ਪੱਕਾ ਜਵਾਬ ਲੱਭਣਾ ਨਾਮੁਮਕਿਨ ਹੈ ਪਰ ਇਹ ਸੰਭਵ ਹੈ ਕਿ ਜਦੋਂ ਪੱਥਰਾਂ ਨਾਲ ਜ਼ਮੀਨ ਉੱਤੇ ਵਾਹ ਕੇ ਹਿਸਾਬ ਕੀਤਾ ਜਾਂਦਾ ਸੀ ਤਾਂ ਇਸ ਗੋਲ ਸੂਚਕ ਦੀ ਵਰਤੋਂ ਹੋਣ ਲੱਗੀ।
ਜਦੋਂ ਕਿਸੇ ਸੰਖਿਆ ਵਿੱਚੋਂ ਘਟਾਓ ਹੁੰਦਾ ਸੀ ਤਾਂ ਖਾਲੀ ਥਾਂ 'ਤੇ ਗੋਲਾ ਵਾਹ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ। ਇਸ ਦਾ ਮਤਲਬ ਸੀ ਕਿ ਇਹ ਸੰਖਿਆ ਹੁਣ ਇੱਥੋਂ ਘਟਾ ਦਿੱਤੀ ਗਈ ਹੈ।
ਇਹ ਵੀ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਕਿ 'ਸ਼ੂਨਿਆ' ਦਾ ਸਾਡੀ ਸੱਭਿਅਤਾ ਨਾਲ ਵੀ ਰਿਸ਼ਤਾ ਹੈ।
'ਸ਼ੂਨਿਆ' ਸੰਸਕ੍ਰਿਤ ਦਾ ਸ਼ਬਦ ਹੈ ਜਿਸ ਦਾ ਮਤਲਬ ਹੈ ਖ਼ਲਾਅ ਜਾਂ ਖਾਲੀ ਥਾਂ। ਭਾਰਤ ਦੀਆਂ ਪ੍ਰਾਚੀਨ ਧਾਰਮਿਕ ਮਾਨਤਾਵਾਂ ਵਿੱਚ 'ਖਾਲੀਪਨ' ਅਤੇ ਮਨ ਵਿੱਚ ਖਿਆਲਾਂ ਨੂੰ ਸ਼ਾਂਤ ਕਰ ਕੇ ਖਾਲੀ ਸਥਾਨ ਪੈਦਾ ਕਰਨ ਨੂੰ ਬਹੁਤ ਵੱਡਾ ਕੰਮ ਮੰਨਿਆ ਜਾਂਦਾ ਸੀ।
ਨਵੇਂ ਅੰਕ ਲਈ 'ਸ਼ੂਨਿਆ' ਸ਼ਬਦ ਵਰਤਿਆ ਗਿਆ ਜਿਸ ਤੋਂ ਇਹ ਜਾਪਦਾ ਹੈ ਕਿ ਵਾਕਈ ਇਸ ਦਾ ਧਰਮ ਅਤੇ ਫ਼ਿਲਾਸਫ਼ੀ ਨਾਲ ਸਬੰਧ ਸੀ।

ਸਿਫ਼ਰ ਤੋਂ ਅਨੰਤਤਾ
ਭਾਰਤ ਦੇ ਮਸ਼ਹੂਰ ਗਣਿਤ ਜਾਣਕਾਰ ਬ੍ਰਹਮਗੁਪਤ ਨੇ ਸੱਤਵੀਂ ਸਦੀ ਵਿੱਚ ਹੀ ਸਿਫ਼ਰ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਉਲੀਕੀਆਂ ਸਨ।
ਉਨ੍ਹਾਂ ਵੱਲੋਂ ਬਣਾਏ ਅਸੂਲ ਅੱਜ ਵੀ ਗਣਿਤ ਦੇ ਆਧਾਰ ਵਜੋਂ ਪੜ੍ਹਾਏ ਜਾਂਦੇ ਹਨ।
1 + 0 = 1
1 - 0 = 1
1 x 0 = 0
ਬ੍ਰਹਮਗੁਪਤ ਨੂੰ ਚੁਣੌਤੀ ਉਦੋਂ ਮਿਲੀ ਜਦੋਂ 1 ਨੂੰ ਸਿਫ਼ਰ ਨਾਲ ਭਾਗ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ।
ਸਵਾਲ ਖੜ੍ਹਾ ਹੋਇਆ: ਉਹ ਕਿਹੜਾ ਅੰਕ ਹੈ ਜਿਸ ਨੂੰ ਸਿਫ਼ਰ ਨਾਲ ਗੁਣਾ ਕਰੋ ਤਾਂ ਨਤੀਜਾ ਆਵੇ '1'!
ਇਸ ਨਾਲ ਹੀ ਗਣਿਤ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਸਿੱਧਾਂਤ ਲਿਆਉਣਾ ਪਿਆ — ਅਨੰਤਤਾ।
ਇਸੇ ਰਾਹੀਂ ਸਿਫ਼ਰ ਨਾਲ ਭਾਗ ਕਰਨ ਦਾ ਵੀ ਨਤੀਜਾ ਮਿਲ ਗਿਆ। ਇਹ ਕਾਢ ਵੀ ਇੱਕ ਭਾਰਤੀ ਗਣਿਤ ਜਾਣਕਾਰ ਦੀ ਸੀ — ਭਾਸਕਰ, ਜਿਨ੍ਹਾਂ ਨੇ ਬਾਰ੍ਹਵੀਂ ਸਦੀ ਵਿੱਚ ਇਹ ਸਿੱਧਾਂਤ ਲਿਆਉਂਦਾ।

ਤਸਵੀਰ ਸਰੋਤ, Getty Images
ਸਮਝ ਨਹੀਂ ਆਈ!
ਫਰਜ਼ ਕਰੋ, ਤੁਸੀਂ ਇੱਕ ਫਲ ਨੂੰ ਵਿੱਚੋਂ ਕੱਟ ਦਿੱਤਾ। ਤੁਹਾਨੂੰ ਦੋ ਹਿੱਸੇ ਮਿਲੇ। ਜੇ ਤਿੰਨ ਹਿੱਸਿਆਂ ਵਿੱਚ ਕੱਟੋਗੇ ਤਾਂ ਤਿੰਨ ਟੁਕੜੇ ਮਿਲਣਗੇ। ਇਸੇ ਤਰ੍ਹਾਂ ਟੁਕੜੇ ਹੁੰਦੇ ਜਾਣਗੇ।
ਇਹ ਅਨੰਤਤਾ ਤੱਕ ਜਾਵੇਗਾ।
ਇਸੇ ਲਈ ਭਾਸਕਰ ਨੇ ਕਿਹਾ ਕਿ ਜਦੋਂ 1 ਨੂੰ 0 ਨਾਲ ਭਾਗ ਕੀਤਾ ਜਾਵੇ ਤਾਂ ਨਤੀਜਾ ਅਨੰਤ ਹੋਵੇਗਾ।

ਤਸਵੀਰ ਸਰੋਤ, Getty Images
ਸਿਫ਼ਰ ਨਾਲ ਗਣਿਤ ਇਸ ਤੋਂ ਵੀ ਅੱਗੇ ਨਿਕਲਿਆ।
ਇਹ ਤਾਂ ਪਹਿਲਾਂ ਹੀ ਪਤਾ ਸੀ ਕਿ 3 ਵਿੱਚੋਂ 3 ਘਟਾਓ ਤਾਂ ਸਿਫ਼ਰ ਨਤੀਜਾ ਆਵੇਗਾ। ਹੁਣ ਜੇ 3 ਵਿੱਚੋਂ 4 ਘਟਾਓ ਤਾਂ?
ਇੱਥੋਂ ਭਾਰਤੀਆਂ ਨੇ ਹਿਸਾਬ ਲਗਾਇਆ ਕਿ ਨੈਗੇਟਿਵ ਨੰਬਰ ਭਾਵ ਰਿਣਾਤਮਕ ਸੰਖਿਆ ਦਾ ਸਿੱਧਾਂਤ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ।
ਭਾਰਤੀ ਸੋਚ-ਵਿਚਾਰ ਵਿੱਚ ਸੰਖਿਆ ਕੇਵਲ ਆਪਣੇ ਮੁੱਲ ਕਰਕੇ ਹੀ ਨਹੀਂ ਜਾਣੀ ਜਾਂਦੀ ਸੀ ਸਗੋਂ ਉਸ ਦਾ ਕੋਈ ਵੀ ਕਰ ਹੋ ਸਕਦਾ ਸੀ।
ਇਸ ਵਿਚਾਰ ਨੇ ਤਾਂ ਗਣਿਤ ਦੀ ਦੁਨੀਆਂ ਵਿੱਚ ਨਵੇਂ ਸਿੱਧਾਂਤਾਂ ਦੀ ਹਨ੍ਹੇਰੀ ਲੈ ਆਉਂਦੀ।

ਤਸਵੀਰ ਸਰੋਤ, Getty Images
'ਐਕਸ' ਅਤੇ 'ਵਾਈ'
ਸੰਖਿਆ ਨੂੰ ਮੁੱਲ ਤੋਂ ਆਜ਼ਾਦ ਕਰਨ ਦੇ ਇਸ ਤੱਥ ਰਾਹੀਂ ਸਵਾਲਾਂ ਨੂੰ ਸੁਲਝਾਉਣ ਦੇ ਨਵੇਂ ਤਰੀਕੇ ਪੈਦਾ ਹੋਏ।
ਇਸੇ ਤਰ੍ਹਾਂ ਸੰਖਿਆ ਦੀ ਥਾਂ 'ਐਕਸ' ਮੰਨ ਕੇ ਜਵਾਬ ਲੱਭੇ ਜਾਣ ਲੱਗੇ।
ਪੱਛਮੀ ਸੱਭਿਅਤਾ ਨੇ ਤਾਂ ਇਸ ਨੂੰ 1657 ਵਿੱਚ ਵਰਤਿਆ ਜਦੋਂ ਫਰਾਂਸ ਦੇ ਗਣਿਤ ਮਾਹਿਰ, ਪਿਏਰ ਦਿ ਫੇਰਮਾ ਨੇ ਇਹ ਤਰੀਕਾ ਸਾਹਮਣੇ ਲਿਆਂਦਾ।
ਉਨ੍ਹਾਂ ਨੂੰ ਸ਼ਾਇਦ ਇਹ ਨਹੀਂ ਪਤਾ ਸੀ ਕਿ ਬ੍ਰਹਮਗੁਪਤ ਨੇ ਹਜ਼ਾਰ ਸਾਲ ਪਹਿਲਾਂ ਹੀ ਇਸ ਦੀ ਵਰਤੋਂ ਕਰ ਲਈ ਸੀ।
ਬ੍ਰਹਮਗੁਪਤ ਨੇ ਇੰਝ ਲੱਭੇ ਜਾਣ ਵਾਲੇ ਜਵਾਬ ਲਈ ਰੰਗਾਂ ਦੇ ਨਾਮ ਦੇ ਪਹਿਲੇ ਅੱਖਰ ਨੂੰ ਵਰਤਣਾ ਸ਼ੁਰੂ ਕੀਤਾ।
ਇੱਥੋਂ ਹੀ ਬਾਅਦ ਵਿੱਚ 'ਐਕਸ' ਤੇ 'ਵਾਈ' ਵਰਗੇ ਅੱਖਰ ਵਰਤਣ ਦਾ ਰਿਵਾਜ਼ ਪਿਆ।

ਤਸਵੀਰ ਸਰੋਤ, Getty Images
ਇੱਥੇ ਅੰਤ ਨਹੀਂ ਹੋਇਆ
ਭਾਰਤੀਆਂ ਨੇ ਹੀ ਟ੍ਰਿਗਨੋਮੈਟਰੀ (ਤਿਕੋਣਮਿਤੀ) ਦੇ ਖੇਤਰ ਵਿੱਚ ਨਵੀਆਂ ਖੋਜਾਂ ਕੀਤੀਆਂ।
ਇੱਹ ਸੱਚ ਹੈ ਕਿ ਯੂਨਾਨੀ ਵਿਦਵਾਨਾਂ ਨੇ ਰੇਖਾ ਗਣਿਤ ਨੂੰ ਸੰਖਿਆਵਾਂ ਨਾਲ ਜੋੜਿਆ ਸੀ।
ਭਾਰਤੀਆਂ ਨੇ ਇਸ ਨੂੰ ਅਗਾਂਹ ਵਧਾਇਆ। ਤਿਕੋਨ ਵਿਗਿਆਨ ਰਾਹੀਂ ਉਨ੍ਹਾਂ ਨੇ ਸਮੁੰਦਰੀ ਦੂਰੀਆਂ ਮਾਪੀਆਂ ਅਤੇ ਪੁਲਾੜ ਦਾ ਵੀ ਵਿਸ਼ਲੇਸ਼ਣ ਕੀਤਾ।
ਭਾਰਤੀਆਂ ਨੇ ਇਸ ਰਾਹੀਂ ਧਰਤੀ ਅਤੇ ਚੰਨ ਵਿਚਕਾਰ ਅਤੇ ਧਰਤੀ ਤੇ ਸੂਰਜ ਵਿਚਕਾਰ ਦੂਰੀਆਂ ਦਾ ਹਿਸਾਬ ਲਗਾਇਆ।

ਭਾਰਤੀ ਗਣਿਤ ਮਾਹਿਰਾਂ ਨੇ ਹੀ ਗਣਿਤ ਦੀ ਸਭ ਤੋਂ ਵੱਡੀ ਗੁੱਥੀ ਸੁਲਝਾਈ ਸੀ, ਜਿਸ ਦਾ ਨਾਂ ਹੈ 'ਪਾਈ'।
ਜਦੋਂ ਇੱਕ ਗੋਲਤਾਰੇ (ਸਰਕਲ) ਦੀ ਘੇਰਾਬੰਦੀ (ਸਰਕਮਫਰੈਂਸ) ਨੂੰ ਉਸ ਦੇ ਵਿਆਸ (ਡਾਇਆਮੀਟਰ) ਨਾਲ ਗੁਣਾ ਕਰ ਦਿੱਤਾ ਜਾਵੇ ਤਾਂ ਜਵਾਬ ਆਉਂਦਾ ਹੈ 'ਪਾਈ'।
ਇਸ ਦੀ ਵਰਤੋਂ ਹਰ ਉਸ ਹਿਸਾਬ ਵਿੱਚ ਕਰਨੀ ਪੈਂਦੀ ਹੈ ਜਿਸ ਵਿੱਚ ਕਿਸੇ ਤਰ੍ਹਾਂ ਗੋਲੇ ਦਾ ਕੋਈ ਸਬੰਧ ਹੋਵੇ, ਜਿਵੇਂ ਇਮਾਰਤਾਂ ਬਣਾਉਣ ਅਤੇ ਸੜਕਾਂ ਵਿਛਾਉਣ 'ਚ।
ਕਈ ਸਦੀਆਂ ਤੱਕ ਵਿਗਿਆਨੀ ਇਸ ਦੀ ਅਸਲ ਸੰਖਿਆ ਲੱਭਦੇ ਰਹੇ।
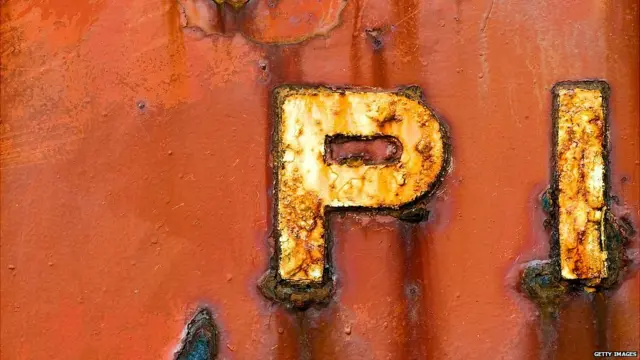
ਤਸਵੀਰ ਸਰੋਤ, Getty Images
ਛੇਵੀਂ ਸਦੀ ਵਿੱਚ ਇੱਕ ਭਾਰਤੀ, ਆਰਿਆਭੱਟ ਨੇ ਇਸ ਦਾ ਠੀਕ ਅੰਦਾਜ਼ਾ — 3.1416 — ਲਗਾਇਆ।
ਆਰਿਆਭੱਟ ਨੇ ਤਾਂ ਧਰਤੀ ਦਾ ਘੇਰ ਵੀ ਲਗਭਗ ਸਹੀ ਮਾਪ ਲਿਆ ਸੀ, ਉਨ੍ਹਾਂ ਮੁਤਾਬਕ ਇਹ 39,968 ਕਿਲੋਮੀਟਰ ਸੀ, ਅਸਲ 'ਚ ਇਹ ਜ਼ਰਾ ਜਿਹਾ ਵੱਧ, 40,075 ਹੈ।
'ਪਾਈ' ਦਾ ਸਹੀ ਅੰਕੜਾ ਜਾਣਨ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਤਰੀਕਾ ਮਾਧਵ ਦਾ ਹੈ। ਇਸ ਫਾਰਮੂਲੇ ਨੂੰ ਜਰਮਨੀ ਦੇ ਇੱਕ ਵਿਗਿਆਨੀ ਦਾ ਮੰਨ ਕੇ ਅੱਜ ਵੀ ਪੜ੍ਹਾਇਆ ਜਾਂਦਾ ਹੈ।
ਇਹ ਵੀਡੀਓ ਵੀ ਜ਼ਰੂਰ ਦੇਖੋ
ਇਸ ਲੇਖ ਵਿੱਚ Google YouTube ਤੋਂ ਮਿਲੀ ਸਮੱਗਰੀ ਸ਼ਾਮਲ ਹੈ। ਕੁਝ ਵੀ ਡਾਊਨਲੋਡ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਅਸੀਂ ਤੁਹਾਡੀ ਇਜਾਜ਼ਤ ਮੰਗਦੇ ਹਾਂ ਕਿਉਂਕਿ ਇਸ ਵਿੱਚ ਕੁਕੀਜ਼ ਅਤੇ ਦੂਜੀਆਂ ਤਕਨੀਕਾਂ ਦਾ ਇਸਤੇਮਾਲ ਕੀਤਾ ਹੋ ਸਕਦਾ ਹੈ। ਤੁਸੀਂ ਸਵੀਕਾਰ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ Google YouTube ਕੁਕੀ ਪਾਲਿਸੀ ਤੇ ਨੂੰ ਪੜ੍ਹਨਾ ਚਾਹੋਗੇ। ਇਸ ਸਮੱਗਰੀ ਨੂੰ ਦੇਖਣ ਲਈ ਇਜਾਜ਼ਤ ਦੇਵੋ ਤੇ ਜਾਰੀ ਰੱਖੋ ਨੂੰ ਚੁਣੋ।
End of YouTube post, 1
ਇਸ ਲੇਖ ਵਿੱਚ Google YouTube ਤੋਂ ਮਿਲੀ ਸਮੱਗਰੀ ਸ਼ਾਮਲ ਹੈ। ਕੁਝ ਵੀ ਡਾਊਨਲੋਡ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਅਸੀਂ ਤੁਹਾਡੀ ਇਜਾਜ਼ਤ ਮੰਗਦੇ ਹਾਂ ਕਿਉਂਕਿ ਇਸ ਵਿੱਚ ਕੁਕੀਜ਼ ਅਤੇ ਦੂਜੀਆਂ ਤਕਨੀਕਾਂ ਦਾ ਇਸਤੇਮਾਲ ਕੀਤਾ ਹੋ ਸਕਦਾ ਹੈ। ਤੁਸੀਂ ਸਵੀਕਾਰ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ Google YouTube ਕੁਕੀ ਪਾਲਿਸੀ ਤੇ ਨੂੰ ਪੜ੍ਹਨਾ ਚਾਹੋਗੇ। ਇਸ ਸਮੱਗਰੀ ਨੂੰ ਦੇਖਣ ਲਈ ਇਜਾਜ਼ਤ ਦੇਵੋ ਤੇ ਜਾਰੀ ਰੱਖੋ ਨੂੰ ਚੁਣੋ।
End of YouTube post, 2