Математика: Између бројева и стварности

Помислите само на Нептун. Зашто? Зато што је, на први поглед, невидљив.

Чак и уз помоћ доброг телескопа.

На 4.3 милијарде километара од Земље, осма планета нашег Сунчевог система изгледа као бела тачкица на небу.

Због тога су нас планете које су ближе Земљи, као што су Венера или Марс - а које толико јарко блеште на ноћном небу - од давнина одушевљавале.

За разлику од њих, за постојање Нептуна сазнало се тек у 19. веку.

Откриће ове планете било је важно из два разлога.

Уран и Нептун

Не само да смо пронашли новог суседа, већ је „Нептун обележио почетак нашег истраживања Сунчевог система, зато што није откривен гледањем у небо нашим очима или уз помоћ телескопа", каже Луси Грин, астрофизичарка из Малардове свемирске научне лабораторије са Универзитетског колеџа у Лондону.

Нептун је откривен захваљујући математици.

У деветнаестом веку, правилно су схваћени Њутнови закони гравитације, а са њима су могле да се предвиде и орбите планета које се обрћу око Сунца.

Сем орбите Урана - откривено је да она благо одступа од очекиване путање.

У оно време, то је била најдаља позната планета од Сунца и неки научници су спекулисали да можда Њутнови закони гравитације не функционишу на толикој удаљености.

Али други су се поуздали у математику и схватили да у близини Урана мора да постоји некакво огромно тело које мења путању ове планете око Сунца.

„Они су израчунали шта, како и где. И кад су усмерили телескоп у правцу области на коју је указала математика, откривена је нова планета", каже Грин.

Откриће Нептуна забележено је у историји као доказ да математика није измишљена, већ да постоји.

И управо је то заинтригирало слушаоца ББЦ емисије КраудСајенс Серђа Хуаркајуа из Перуа.

„Од Галилеја који је могао да предвиди брзину лопте док се котрља низ падину, до, на пример, постојања Хигсовог бозона, предвиђеног математиком пре него што је честица пронађена у стварности, та моћ да се предвиди постојање ствари које нису виђене голим оком делује ми фантастично", написао је он.

„Да ли је математика модел, опис, метафора за стварност... или је она стварност сама?"

Ово питање хиљадама година мучи и филозофе - и даље је узрок великог неслагања.

Не постоји негативна торта

Готово је сигурно да су људи почели да се баве математиком из овоземаљских разлога, као што је пребројавање и мерење ствари, тако да почнимо одатле.

Узмимо као пример торту.

Математика може да нам саопшти свакакве ствари о тој торти: њене димензије, тежину, како је распарчати - и све то на врло опипљив начин.

А торта може да нам покаже да математика допире тамо где стварност не досеже.

Уколико поједете трећину торте, остале су вам две трећине.

За сада је све како треба. Ако поједете и преосталу трећину, па још једну, не остаје вам ништа.

„Ми описујемо менталне контуре наших предака", каже Алекс Белос, аутор математичких књига.

„Они су користили практичну математику да би мерили и бројали, али нису стигли до негативних бројева."

Ако се ваш концепт стварности састоји од предмета које можете да измерите и пребројите, тешко вам је да замислите било шта што је мање од нуле.

О дуговима и негативним бројевима

Чим поједете и последње мрвице те торте, готово је: не постоји негативна торта.

Међутим, каже Белос, постоји област у којој користите негативне бројеве и потпуно је природно да размишљате о њима.

Белос говори о новцу.

„Можете да поседујете новац, али исто тако можете и да га дугујете. Прва практична употреба негативних бројева била је у контексту банковних рачуна и дуговања", каже он.

Уколико дугујете пет долара, а ја вам дам ту суму, имаћете нула долара.

На тај начин стварност почиње са негативним бројевима.

Данас је тешко размишљати о математици без њих и то не само када се ради о дуговањима.

За сада смо и даље дубоко укорењени у стварности.

Али кад кренете да се играте са негативним бројевима, почињу да се дешавају неке врло необичне ствари.

Огромна енигма

Ако помножите два таква броја, резултат је позитиван број.

Дакле -1 x -1 = 1 и тако стижемо до истинске енигме.

„Ако почнете да се играте с једначинама које садрже и негативне и позитивне бројеве, стићи ћете до:

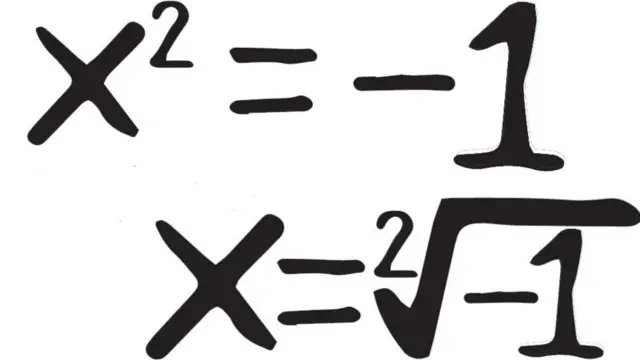
„Шта ли је то? Како кад квадрирате нешто стижете до резултата -1!", каже Белос.

„То не може да буде позитиван број јер кад га квадрирате - илити помножите са самим собом - резултат је позитиван број; а не може да буде ни негативан број, из истог тог разлога", каже он.

„Кад се то десило први пут, људи су мислили да се ради о апсурду."

„Али, мало по мало, математичари су почели да говоре: 'Јесте, апсурдно је, али кад то користим у раду, добијам прави одговор. Препустимо филозофима да прокљуве шта би то могло да буде. Нама математичарима потребни су одговори и, уколико нам то помогне да их нађемо, онда је то у реду."

И управо смо сада напустили стварност.

Али, у сваком случају, математика и даље служе објашњава врло стваран свет у ком живимо.

Имагинарно

„Квадратни корен из -1 зове се 'имагинарни број', што је ужасно име зато што стичете утисак да је математика до тог тренутка била реална, а онда је одједном постала имагинарна", каже Белос.

„Не, математика је од самог почетка имагинарна. Можемо да говоримо о три торте, али ми видимо само торте, не видимо 'три': три је апстракција", истиче он.

„Исто вам је кад имате имагинарне бројеве. Делује потпуно лудо, али чим почнете да разумете како се они уклапају, све постаје логично. И понашање онога што зовемо реалним бројевима са имагинарним бројевима - све до нечега што зовемо сложеним бројевима, бриљантан је речник да се опишу ствари као што је ротација."

„Ових дана, квадратни корен од -1 реалан је колико и сам -1", чак и ако нам је тешко да разумемо -1, баш као што је то било нашим прецима.

Само без панике

Ако сте се мало погубили, ништа не брините - само наставите да читате и све ће вам бити јасно. Заиста.

Сложени бројеви омогућавају решења неких једначина које немају решења у реалним бројевима.

Они су невероватно практични за разумевање стварности и служе као алатке за готово све што укључује ротацију или таласе.

Користе се у електротехници, радарима, медицинским снимањима и могу да се примене на разумевање субатомских честица.

Али како то да нешто што изгледа као да постоји само у математичким сновима на крају испадне толико корисно у стварном свету?

За неке, као што је мађарски физичар из двадесетог века Јуџин Вигнер, то представља скоро па чудо.

Вигнер се позвао на сложене бројеве у утицајном есеју из 1960. године, Неразумна ефикасност математике у природним наукама.

Неразумна ефикасност

Али ако су људи осмислили математику управо да би описали стварност, зар није онда логично што она то и ради? Шта је неразумно у вези с тим?

Обратимо се сада некоме ко се непрестано креће између филозофије и математике: експерту за филозофију физике Еленор Нокс.

„Уколико смо изумели математику да би нам помогла да разумемо физичке системе, истина је да је веома логично да она то и ради. Али чини се да се математика испочетка није развијала на тај начин", објашњава она.

„Има много случајева у којима су математичари урадили нешто само зато што су били заинтересовани за то, а у неком каснијем периоду испоставило се да је управо то било неопходно за неко кључно откриће у физици.

„Славан пример је нееуклидска геометрија", каже Нокс, говорећи о грани геометрије којом су се бавили многи математичари крајем 19. века - пре свега зато што су мислили да је интересантна.

„Мислили су да читав наш свет може да се опише преко еуклидске геометрије, оне коју учите у школи. Правила правог угла, да углови троугла у збиру дају 180 степени, на пример."

Математичари деветнаестог века нису се бацили на обарање еуклидске геометрије. Просто су само истраживали и пронашли неке занимљиве математичке структуре.

„У двадесетом веку, кад је Алберту Ајнштајну била потребна теорија којом би описао правила простора и времена за општу теорију релативности, управо му је помогла нееуклидска геометрија - он просто не би успео да није било ње", додаје Нокс.

„Данас ми мислимо да свет има структуру те геометрије која је некада била крајње необична, а ниједан математичар који је кренуо да ради на њој није предвидео то конкретно откриће", закључује она.

Такви случајеви нас наводе на размишљање да, уколико није баш чудноват, однос математике према стварности макар је поприлично запањујућ.

Фундаментална стварност

Имајући у виду правац у ком се развија модерна физика, нама обичним смртницима тешко је да разумемо компликовану математику и необичну стварност коју она описује.

Али то можда и не изненађује: не постоји разлог зашто би свакодневна стварност коју доживљавамо путем наших чула била фундаментална стварност универзума.

Оно што изненађује је да се чини да математика уме да истражи много више него што нам наша чула допуштају.

Међутим, у потрази за фундаменталном стварношћу, хоће ли се десити да математика досегне максимум способности да је опише?

„Двадесети век нам је подарио две од наших најуспешнијих физичких теорија: квантну механику (свет на нивоу ултра-малог, атома и субатома) и теорију опште релативности", каже Нокс.

„Испоставља се да је постизање тога да математика обједини те две теорије изузетно компликовано."

„Немамо кохерентан оквир за разумевање тога како те две теорије могу да функционишу у истом свету - како оне могу да опишу исту стварност", додаје она.

„Морате да се изборите са запањујућим нивоима сложености а да не успете, за сада, да спојите оно што сте промислили са експериментима."

Међутим, као што смо већ видели раније, много тога је започело управо тако: као идеја у потрази за практичном функцијом.

Али да ли смо сада можда ударили у зид?

„У овом тренутку, човек би лако могао да закључи да смо до сада имали веома, веома много среће што је математика успевала да опише наш универзум", каже Нокс.

„Друга опција је да помислите како математика описује само делове света, али не и њега у целости."

„Или можда да је разумевање света у његовој целости веома компликовано."

„Или да је математика врашки компликована, да је превише за нас или да је још нисмо разумели, али да једног дана хоћемо", каже она.

Велика разлика

Можда и не би требало да нас изненади што је понекад ђаволски тешко ускладити математичке законе са законима физичке стварности. На крају крајева, они нису исто.

Као што је Ајнштајн једном рекао: „Што се више односе на стварност, математички закони више постају несигурни; а што су сигурнији, мање се односе на стварност."

Нокс објашњава: „Математика има једну посебну карактеристику: апсолутно је истинита или неистинита. Ако докажем нешто у математици, нико не може да оповргне ту чињеницу."

„Физички закони нису такви. То је једна од великих разлика међу њима."

„Често смо грешили у законима. Њутнови закони су предивни, елегантни и у неким случајевима валидни, али они нису комплетна истина. Нема сумње да ће се у будућности показати да су Ајнштајнови закони такође апроксимативни", предвидела је ова филозофкиња физике.

Откривена или измишљена?

Одакле долази математика?

То је питање за математичара.

Јуџинија Ченг је гостујућа научница Школе уметничког института у Чикагу.

Она може да одговори на питање да ли је математика нешто што је откривено или измишљено.

„Заиста мислим да ја откривам концепте а измишљам начине размишљања о њима. Када радим апстрактно истраживање, осећам се као да лутам кроз апстрактну џунглу у потрази за стварима и онда измишљам начин на који ћу да говорим и теоретишем о њима како бих могла да организујем властите мисли и пренесем их другима", каже она.

Ченг ради на пољу Теорије категорија (понекад зване „математиком математике"), која покушава да премости јаз између различитих области у математици.

„Шта је уопште стварно?"

Тешко је замислити нешто апстрактније од тога, тако да смо је питали да ли мисли да се математика коју она проучава односи и на стварност.

„Кад ме људи питају за стварност, ја желим да одговорим са: а шта је уопште стварно?"

„Оно што ми зовемо 'стварношћу' заправо су халуцинације које доживљавамо као стварне зато што смо сви склони да их перципирамо на исти начин."

„Људи кажу да бројеви нису стварни зато што не можете да их додирнете. Али има много ствари које су стварне али не могу да их додирнем, као што је, на пример, глад", објашњава она.

„Зато више волим да говорим о конкретним стварима - онима које можемо да додирнемо и са којима можемо да имамо директну интеракцију - и о апстрактним стварима - са којима имамо интеракцију у нашем мозгу."

„Математика је апстрактна, али апстрактна идеја може да буде онолико стварна као и било шта друго."

Шта је стварно?

С једне стране, неко може да тврди да је математика стварност.

Помислите само, на пример, на нашу биологију, која се састоји од хемије, а којом суштински владају физички закони... и ми тако стижемо до бројева.

Или помислите на плаво небо, које се објашњава таласним дужинама преламања светлости... и све су то бројеви.

Чини се да је, ако закопате довољно дубоко, физичка стварност суштински математичка.

Чини се да математика, међутим, не може да нам каже ништа значајно о неким од најважнијих животних питања, као што су љубав, глад или смртност.

И тако, од свих стварно великих питања, са сигурношћу можемо да одговоримо на само једно: можда нећемо успети да нађемо коначне одговоре на питање које је поставио Серђо Хуаркаја из Перуа.

Заправо, сада са сигурношћу можемо да кажемо да нећемо.

Али их је зато вредело тражити.

Пратите нас на Фејсбуку и Твитеру. Ако имате предлог теме за нас, јавите се на [email protected]