Key points about combined transformations and invariant points

To plot a combined transformationA transformation changes the position or size of a shape., complete the first step, then apply the second step to the new imageThe resultant position of a shape after a transformation. of the shape, eg a reflectionA transformation of a shape which results in a mirror image of the shape with respect to a line. followed by a translationThe movement of a shape from one place to another. The shape has the same orientation..
A combination of transformations can sometimes be described using a single transformation, eg when a shape is transformed by two consecutive translations, the result can be expressed as a single translation vector.
If a vertex does not change position under a single or a series of transformations, it is called an invariant point.
Make sure you are confident at working with translations, reflections, rotations and enlargements on a set of axes, to understand combined transformations.
What are invariant points?
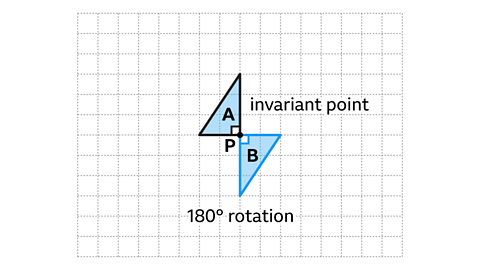
An invariant pointA vertex that does not change position after a transformation is applied. is a vertexThe point at which two or more lines cross. The corner of a shape. The plural form is vertices. that does not change position under a single or a series of transformations.
For example, if a shape is reflected in a line and there are vertices of the shape lying on the line, they will be invariant under this transformation.
For a rotationA transformation of a shape which results in a turning effect on the shape., the only invariant point is the centre of rotationA fixed point about which a shape is rotated..
For an enlargementA transformation of a shape which results in a shape increasing or decreasing in size., the only invariant point is the centre of enlargementA point which defines the position of an enlarged shape..

Follow the worked example below
GCSE exam-style questions
- Enlarge triangle ABC by a scale factor 3. Use the point with coordinates (−4, −5) as the centre of enlargement.
Work out the position of the enlargement using paper, a pencil and ruler.
Identify any invariant points.
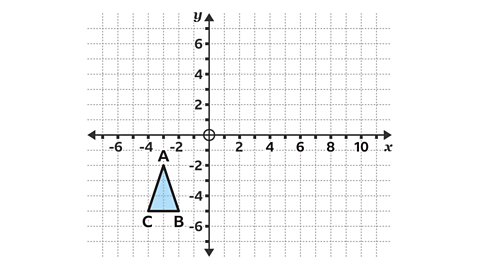
Vertex C, at (−4, −5) is an invariant point.
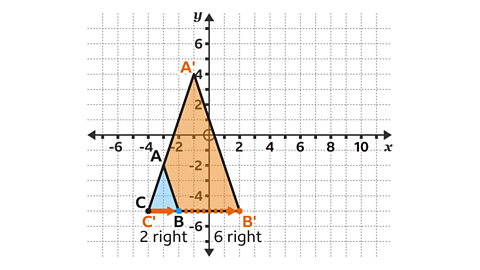
- Calculate the position of each new vertex.
For example, vertex B at (−2, −5) is two squares to the right of the centre of enlargement.
- Multiply this displacement by the scale factor of 3.
3 × 2 = 6
The corresponding point needs to be six squares to the right of the centre of enlargement. The corresponding point has coordinates (2, −5).
- Repeat for the other two vertices.
Vertex C lies on the centre of the enlargement. This point is invariant under the enlargement.
- Reflect triangle DEF in the line 𝑦 = 1
Work out the position of the reflection using paper, a pencil and ruler.
Identify any invariant points.
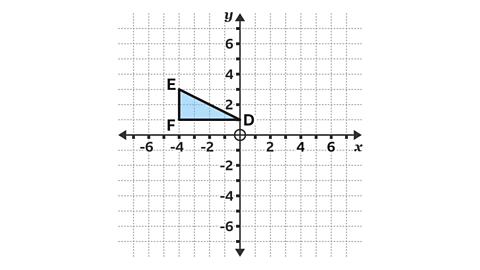
Vertex D, at (0, 1) and vertex F, at (−4, 1) are invariant points.
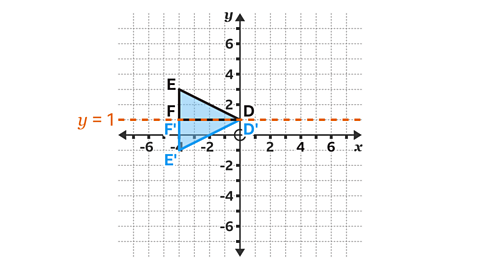
The line 𝑦 = 1 is a horizontal line which passes through the 𝑦 axis at 1.
Vertex E is two squares above the line of reflection. The corresponding vertex is two squares below the line of reflection. It has coordinate coordinates (−4, −1).
Vertices D and F lie on the line of reflection. These points are invariant under the reflection.
How to plot a combined transformation
Sometimes a shape is transformed using more than one step, such as a reflection followed by a rotation.
A combination of transformations can be described as a single transformation. For example, a combination of two reflections can be expressed as a rotation.
A combined transformation for a shape is completed by applying the first transformation and then applying the second step to the new image.
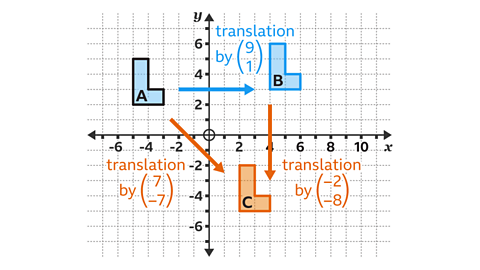
For example, translating shape A nine squares to the right and one square up (to shape B), followed by a translation of two squares to the left and eight squares down (to shape C) , is equivalent to an overall translation of seven squares to the right and seven squares down.

Follow the worked example below
GCSE exam-style questions
- Reflect shape A in the line 𝑦 = −1
Label the result B.
Reflect shape B in the 𝑦-axis.
Label the result C.
What are the coordinates of the vertices in shape C ?
Work out the position of the reflections using paper, a pencil and ruler.
The coordinates of shape C are (−3, −3), (−4, −6) and (−6, −5)
The line 𝑦 = −1 is a horizontal line which passes through the 𝑦-axis at −1.
The position of each new vertex in shape B can be calculated.
For example, the vertex at (3, 1), on shape A, is two squares above the line of reflection. Therefore, the corresponding vertex on shape B must be two squares below the line of reflection.
The corresponding vertex on shape B has the coordinate (3, −3).
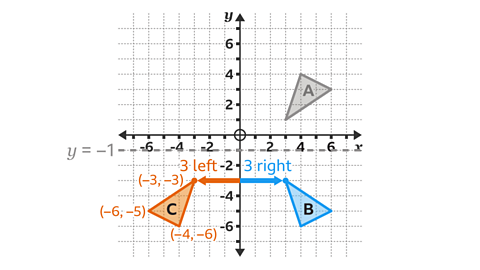
Calculate the position of each new vertex in shape C by reflecting shape B in the 𝑦-axis.
For example, the vertex at (3, −3), on shape B, is three squares to the right of the 𝑦-axis.
Therefore, the corresponding vertex on shape C must be three squares to the left of the 𝑦-axis.
The corresponding vertex on shape C has coordinate
(−3, −3).
- Reflect shape D in the line 𝑦 = 𝑥.
Label the result E.
Translate shape E by the vector in the image.
Label the result F.
What are the coordinates of the vertices in shape F?
Work out the position of the reflections using paper, a pencil and ruler.
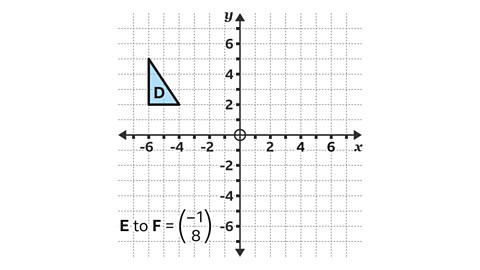
The coordinates of shape F are (1, 2), (4, 2) and (1, 4).
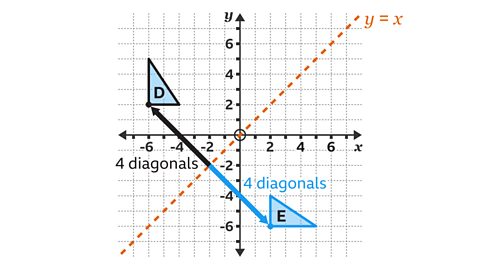
The line 𝑦 = 𝑥 is a diagonal line which passes through the points (−6, −6) and (6, 6).
The position of each new vertex in shape E can be calculated.
For example, the vertex at (−6, 2), is at a distance of four diagonals of a square from the line of reflection.
Therefore, the corresponding vertex in shape E is at a distance of four diagonals from the line of reflection on the opposite side.
The corresponding vertex on shape E has the coordinate (2, −6).
The vector in the image means the shape E is translated 1 square to the left and 8 squares up.
This is a horizontal displacement of −1 and a vertical displacement of 8.
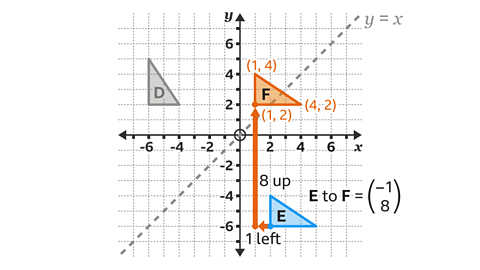
The position of each new vertex in shape F can be calculated.
For example, the vertex at (2, −6) moves 1 square to the left and 8 squares up.
The corresponding vertex on shape F has the coordinate (1, 2).
Check your understanding
How to describe a combined transformation
The combination of transformations can sometimes be described as a single transformation.
To describe the transformation, identify what type of transformation it is.

For a translation, give the translation vector.
For a reflection, give the equation for the line of reflection.
For a rotation, give the angle, direction and coordinates of the centre of rotation.
For an enlargement, give the scale factor, and a coordinate for the centre of enlargement.
Follow the worked example below
Interactive activity – Reflections
This interactive activity will help you understand how two reflections can combine across two intersecting lines to be the same as a single rotation.
GCSE exam-style questions
- Shape P is transformed on to Shape Q by a reflection in the line 𝑦 = 2.
Shape Q is transformed on to Shape R by a reflection in the line 𝑦 = 𝑥.
What single transformation takes shape P to shape R?
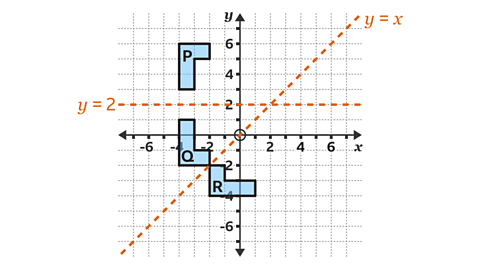
Shape R is a rotation of shape P 90° anti-clockwise (or 270° clockwise) about the point (2, 2).
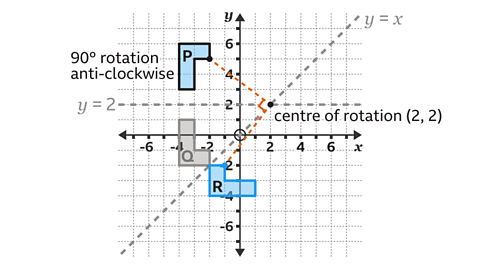
By comparing shapes P and R, the type of transformation can be worked out.
The shape has turned, so it is a rotation.
Describe a rotation by giving the angle, direction and a coordinates for the centre of rotation.
The distances from the centre of rotation to the vertices of the original shape, and the corresponding vertices on the rotated shape, are equal.
The lines intersect at 90°, the angle of the rotation.
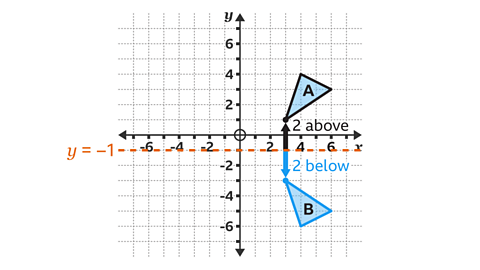
- Shape A is transformed on to Shape B by the given vector in the image above.
Shape B is transformed on to Shape C by the given vector in the image above.
What single transformation takes shape A to shape C?
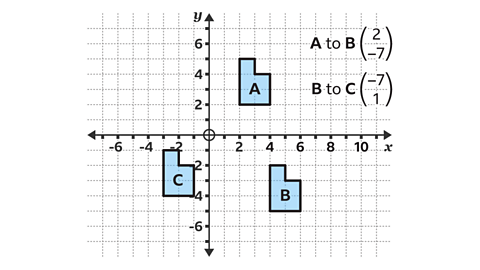
Shape C is a translation of shape A by the given vector in the image above.
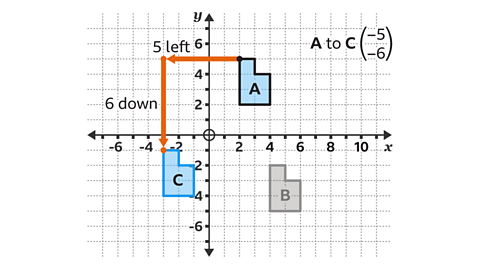
By comparing shape A and C the type of transformation can be worked out.
The shape is not reflected or rotated, and the size of the shape does not change. This means the transformation from triangle A to triangle Cis a translation.
Describe a translation by using a translation vector.
From shape A to shape C, the reference point P has moved 5 square to the left and 6 squares down.
This is a horizontal displacement of −5 and a vertical displacement of −6.
Quiz – Combined transformations and invariant points
Practise what you've learned about combined transformations and invariant points with this quiz.
Now you've revised combined transformations and invariant points, why not take a look at the sine rule?
More on Geometry and measure
Find out more by working through a topic
- count25 of 35

- count26 of 35

- count27 of 35