Key points about solving 2D and 3D problems using Pythagoras' theorem

Pythagoras' theorem states that for any right-angled triangle, the square of the hypotenuseThe longest side in a right-angled triangle. is equal to the sum of the squares of the other two sides.
If the sides of the right-angled triangle are labelled 𝑎, 𝑏 and 𝑐 then Pythagoras' theorem can be written as the formula 𝑎² + 𝑏² = 𝑐².
Pythagoras' theorem can be used to find the length of line segments and applied in two and three dimensions. Using Pythagoras' theorem in 3D is for Higher tier only.
Make sure you are confident in working with Pythagoras' theorem before solving these 2D and 3D problems.
Calculating the length of a line segment
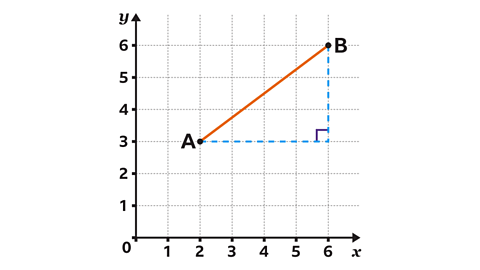
A line segment is a part of a line which has two end points. When plotted on a set of axes, the points at the ends of the line segment can be expressed using coordinatesThe ordered pair of numbers that defines the position of a point..
Find the length of the line segment using Pythagoras' theorem by adding a vertical and horizontal line to form a right-angled triangle.
When just two points, 𝐴 and 𝐵, have been provided it is useful to sketch a diagram.

Follow the worked example below
GCSE exam-style questions

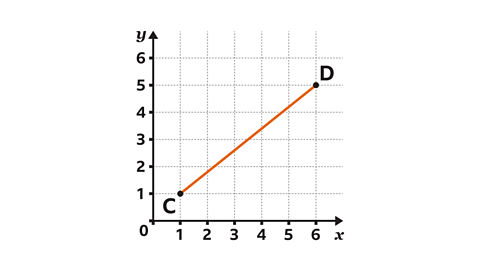
- Point 𝐶 has coordinates (1, 1). Point 𝐷 has coordinates (6, 5).
Use Pythagoras' theorem to find the length of the line segment 𝐶𝐷.
Give the answer to one decimal place.
𝐶𝐷 = 6·4 units to 1 d.p.
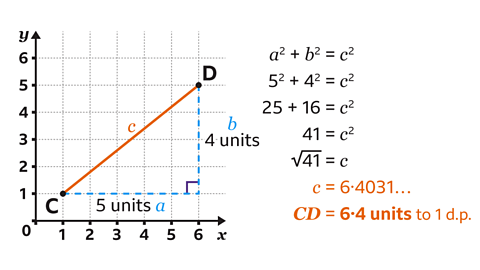
A right-angled triangle is formed by adding a horizontal line from 𝐶 and dropping a vertical line from 𝐷.
The horizontal line measures 5 units. The vertical line measures 4 units.
Two sides of the triangle are known. Pythagoras's theorem is used to find the missing side.
- Label the sides of the triangle 𝑎, 𝑏 and 𝑐.
Remember the hypotenuse, which is opposite the right-angle, should always be labelled 𝑐, The order for 𝑎 and 𝑏 does not matter.
Substitute the values into the equation 𝑎² + 𝑏² = 𝑐².
𝑎² = 5² and 𝑏² = 4².Calculate the value of the squares. 5² = 25 and 4² = 16.
Add the squares together to get 41. This is the value of 𝑐².
The inverse of squaring is square rooting.
- Calculate the square root of 41 to find 𝑐. This gives the answer of 𝑐 = 6.4031.
Therefore, rounding this to one decimal place, the length of 𝐶𝐷 is 6·4 units.
- Point 𝐸 has coordinates ( – 6, 6).
Point 𝐹 has coordinates (6, 1).
Use Pythagoras' theorem to find the length of the line segment 𝐸𝐹.
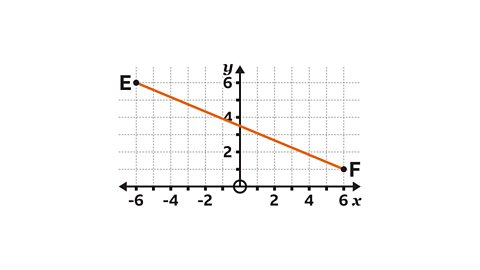
𝐸𝐹 = 13 units
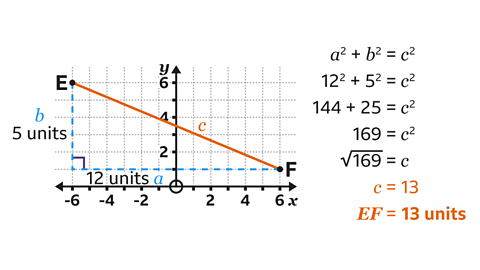
A right-angled triangle is formed by adding a horizontal line from 𝐹 and dropping a vertical line from 𝐸.
The horizontal line measures 12 units.
The vertical line measures 5 units.
Two sides of the triangle are known.
Pythagoras's theorem is used to find the missing side.
- Label the sides of the triangle 𝑎, 𝑏 and 𝑐.
Remember the hypotenuse, which is opposite the right-angle, should always be labelled 𝑐, The order for 𝑎 and 𝑏 does not matter.
Substitute the values into the equation 𝑎² + 𝑏² = 𝑐².
𝑎² = 12² and 𝑏² = 5².Calculate the value of the squares. 12² = 144 and 5² = 25.
Add the squares together to get 169. This is the value of 𝑐².
The inverse of squaring is square rooting.
- Calculate the square root of 169 to find 𝑐. This gives the answer of 𝑐 = 13.
Therefore, the length of 𝐸𝐹 is 13 units.
- Point 𝑃 has coordinates (1, 4).
Point 𝑄 has coordinates (6, 2).
Use Pythagoras' theorem to find the length of the line segment 𝑃𝑄.
Give the answer to one decimal place.
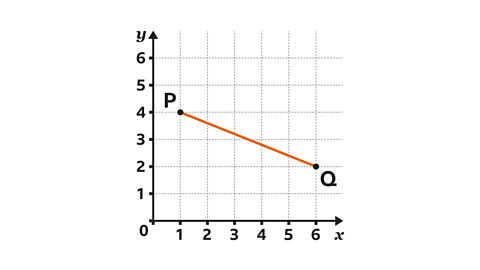
𝑃𝑄 = 5·4 units
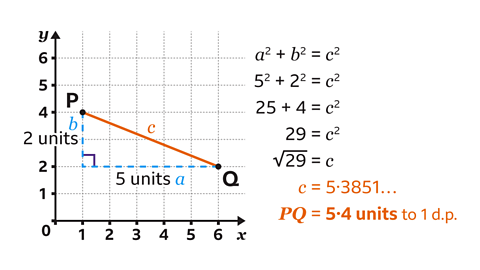
- Sketch a set of axes with 𝑃 at (1, 4) and 𝑄 at (6, 2).
A right-angled triangle is formed by adding a horizontal line from 𝑄 and dropping a vertical line from 𝑃.
The horizontal line measures 5 units.
The vertical line measures 2 units.
Two sides of the triangles are known.
Pythagoras's theorem is used to find the missing side.
- Label the sides of the triangle 𝑎, 𝑏 and 𝑐.
Remember the hypotenuse, which is opposite the right-angle, should always be labelled 𝑐, The order for 𝑎 and 𝑏 does not matter.
Substitute the values into the equation 𝑎² + 𝑏² = 𝑐².
𝑎² = 5² and 𝑏² = 2².Calculate the value of the squares. 5² = 25 and 2² = 4.
Add the squares together to get 29. This is the value of 𝑐².
The inverse of squaring is square rooting.
- Calculate the square root of 29 to find 𝑐. This gives the answer of 𝑐 = 5·3851…
Therefore, rounding this to one decimal place, the length of 𝑃𝑄 is 5·4 units.
Using Pythagoras' theorem in 2D
Pythagoras' theorem can be used to solve 2-dimensional problems which involve calculating a length in a right-angled triangle.
Identify these questions by recognising situations where a side of a right-angled triangle needs to be calculated and two sides are known.
It may be necessary to use Pythagoras' theorem more than once in a problem.

Follow the worked example below
GCSE exam-style questions
- A ladder of length 7 metres leans against a vertical wall.
The base of the ladder is 1·5 metres from the base of the wall.
Work out how far up the wall the ladder reaches.
Give the answer to 1 decimal place.
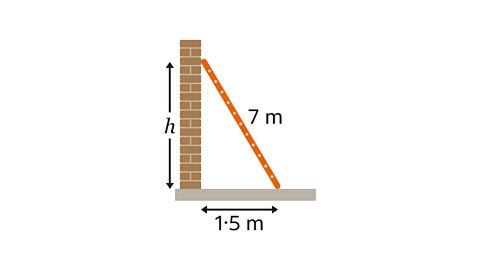
6·8 m to 1 d.p
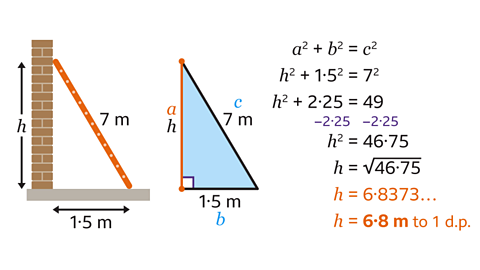
The wall, ladder and floor form a right-angled triangle.
Two sides of the triangle are known. Pythagoras' theorem is used to find the missing side.
Label the sides of the triangle 𝑎, 𝑏 and 𝑐.
Substitute the values into the equation 𝑎² + 𝑏² = 𝑐².
𝑏² = 1·5² and 𝑐² = 7². Replace 𝑎² with ℎ², the variable used in the question.Calculate the value of the squares 1·5² = 2·25 and 7² = 49. This gives the equation ℎ² + 2·25 = 49.
Subtract 2·25 from both sides of the equation to work out the value of ℎ². This leads to the equation ℎ² = 46·75.
Calculate the square root of 46·75 to find 𝑎.
This gives the answer of ℎ = 6·8373…
Therefore, when rounded to 1 decimal place, the height the ladder can reach is 6·8 m.
- A piece of wire is formed into a trapezium shape.
Calculate the total amount of wire needed to make the trapezium.
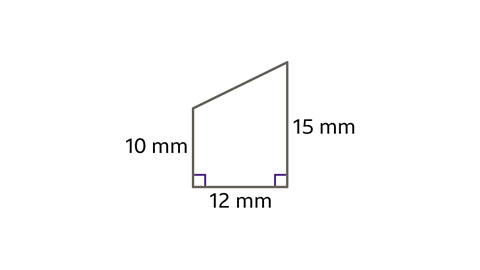
50 mm
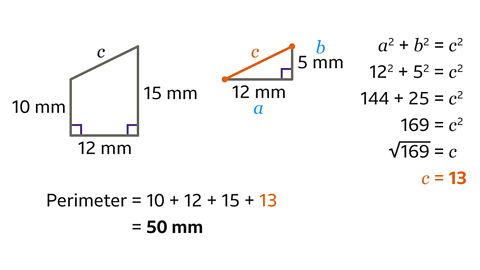
The amount of wire needed to make the trapezium is equivalent to its perimeter.
The length of the unknown side is the hypotenuse of a right-angled triangle with a base measuring 12 mm and a height that is 15 – 10 = 5 mm.
Two sides of the triangle are known. Pythagoras's theorem is used to find the missing side.
- Label the sides of the triangle 𝑎, 𝑏 and 𝑐.
Remember the hypotenuse, which is opposite the right angle, should always be labelled 𝑐. The order for 𝑎 and 𝑏 does not matter.
Substitute the values into the equation 𝑎² + 𝑏² = 𝑐².
𝑎² = 12² and 𝑏² = 5².Calculate the value of the squares. 12² = 144 and 5² = 25.
Add the squares together to get 169. This is the value of 𝑐².
Calculate the square root of 169 to find 𝑐. This gives the answer of 𝑐 = 13 mm.
Add the four sides to find the perimeter.
10 + 12 + 15 + 13 = 50
Quiz – Solving 2D problems using Pythagoras' theorem
Practise what you've learned about solving 2D problems using Pythagoras' theorem with this quiz.
Higher – Using Pythagoras' theorem in 3D
Use Pythagoras' theorem to solve 3-dimensional problems which involve calculating the length of a right-angled triangle.
For example, Pythagoras' theorem can be applied twice to find the distance between two opposite vertices in a cuboid.
When working in three-dimensions, it can be helpful to draw additional diagrams to help visualise the question.
Numbers expressed in questions or final answers may be written as surds.

A surd is an exact answer written as a square root.
To simplify a surd, identify a square number factor.
For example, √12 can be simplified because 4 is a square number factor of 12.
√12 = √4 × √3 = 2√3
Follow the worked example below
GCSE exam-style questions
- A cuboid measures 4 cm × 7 cm × 10 cm.
Calculate the length of 𝐸𝐾.
Give the answer to 1 decimal place.
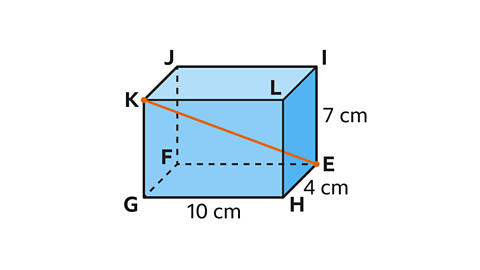
𝐸𝐾 = 12·8 cm.
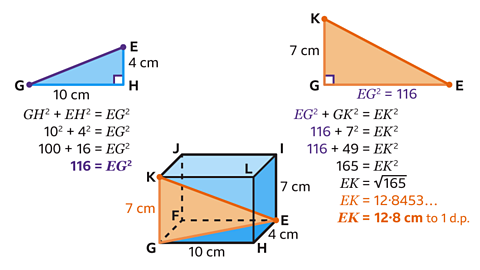
The length 𝐸𝐾 is the hypotenuse of a right-angled triangle, 𝐸𝐾𝐺, with a height 7 cm and unknown base 𝐸𝐺.
The length of 𝐸𝐺 is the hypotenuse of a second right-angled triangle, 𝐸𝐺𝐻, with height 4 cm and a base of
10 cm.
Two sides of the triangle are known.
Pythagoras' theorem is used to find the missing side.
For triangle, 𝐸𝐺𝐻, Pythagoras' theorem states
𝐺𝐻² + 𝐸𝐻² = 𝐸𝐺².
Substitute the values, 𝐺𝐻² = 10² and 𝐸𝐻² = 4², into the formula.
Calculate the value of the squares.10² = 100 and 4² = 16.
Add the squares together to get 116.
This is the value of 𝐸𝐺². 𝐸𝐺 can be calculated but this is unnecessary for the next step.
For triangle, 𝐸𝐾𝐺, Pythagoras' theorem states
𝐸𝐺² + 𝐺𝐾² = 𝐸𝐾².
- Substitute the values into the formula.
From the previous calculation, 𝐸𝐺² = 116 and
𝐺𝐾² = 7² = 49.
Add the values together to get 165. This is the value of 𝐸𝐾².
Calculate the square root of 165 to find 𝐸𝐾.
This gives the answer of 𝐸𝐾 = 12·8453…
Therefore, when rounded to 1 decimal place, 𝐸𝐾 = 12·8 cm.
- A cube has sides measuring 8 cm.
Calculate the length of 𝑥.
Express the answer in the form 𝑎√3 where 𝑎 is an integer.
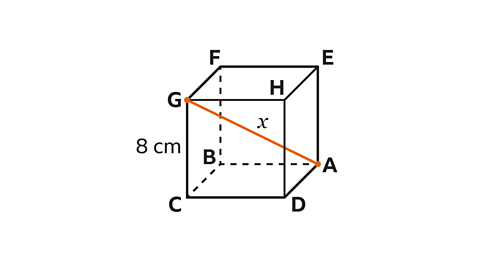
8√3 cm
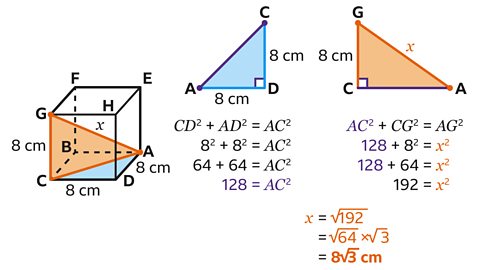
The length of 𝑥 can be calculated by applying Pythagoras' theorem twice.
The length of 𝑥 is the hypotenuse of a right-angled triangle, 𝐴𝐶𝐺, with height 8 cm and unknown base 𝐴𝐶.
The length 𝐴𝐶 is the hypotenuse of a second right-angled triangle, 𝐴𝐶𝐷 , with height 8 cm and base 8 cm.
For triangle, 𝐴𝐶𝐷, Pythagoras' theorem states 𝐶𝐷² + 𝐴𝐷² = 𝐴𝐶².
Substitute the values, 𝐶𝐷² = 8² and 𝐴𝐷² = 8², into the formula.
Calculate the value of the squares. 8² = 64 and 8² = 64.
Add the squares together to get 128. This is the value of 𝐴𝐶².
For triangle, 𝐴𝐶𝐺, Pythagoras' theorem states 𝐴𝐶² + 𝐶𝐺² = 𝐴𝐺².
Substitute the values into the formula. From the previous calculation 𝐴𝐶² = 128 and 𝐶𝐺² = 8² = 64.
Add the values together to get 192. This is the value of 𝑥².
Calculate the square root of 192 to find 𝑥.
Write this as a simplified surd, by finding the largest square number factor of 192.
The largest square number factor of 192 is 64.
𝑥 = √192 = √64 × √3.
- The square root of 64 is 8.
Therefore, 𝑥 = 8√3.
Higher – Quiz – Using Pythagoras' theorem in 3D
Practise what you've learned about using Pythagoras' theorem in 3D with this quiz.
Now you've revised solving 2D and 3D problems with Pythagoras' theorem, why not look at calculations using the alternate segment theorem, tangents and chords?
More on Geometry and measure
Find out more by working through a topic
- count29 of 35

- count30 of 35

- count31 of 35

- count32 of 35
