Key points about Pythagoras' theorem

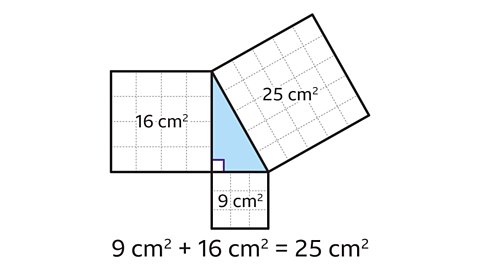
Pythagoras’ theorem states that for any right-angled triangle, the square of the hypotenuseThe longest side in a right-angled triangle. is equal to the sum of the squares of the other two sides.
If the sides of the right-angled triangle are labelled 𝑎, 𝑏 and 𝑐 then Pythagoras' theorem can be written as the formulaA fact, rule, or principle that is expressed in terms of mathematical symbols. The plural of formula is formulae.:
𝑎² + 𝑏² = 𝑐²
Here, 𝑐 represents the hypotenuse.
- Use Pythagoras’ theorem to show a triangle is right-angled or to find one side of a right-angled triangle when two sides are known.
Make sure you are confident at substituting into and manipulating formulae.
Check your understanding
How to calculate the hypotenuse of a right-angled triangle
Use Pythagoras’ theorem to calculate a missing side in a right-angled triangle.
Find the length of the hypotenuseThe longest side in a right-angled triangle. when the other two sides are given by following these steps.
- Label the sides of the triangle 𝑎, 𝑏 and 𝑐.
Remember that the hypotenuse, which is opposite the right-angle, should always be labelled 𝑐.
Substitute the values of 𝑎 and 𝑏 into the formula 𝑎² + 𝑏² = 𝑐².
Calculate the left-hand side of the formulaA fact, rule, or principle that is expressed in terms of mathematical symbols. The plural of formula is formulae. by adding the squares together to get the value of 𝑐².
Square root the value of 𝑐² to work out the value of 𝑐.

Follow the worked example below

A right-angled triangle where all three sides are integers is called a Pythagorean triple.
The 6, 8, 10 triangle in the question above is an example of this.
GCSE exam-style questions
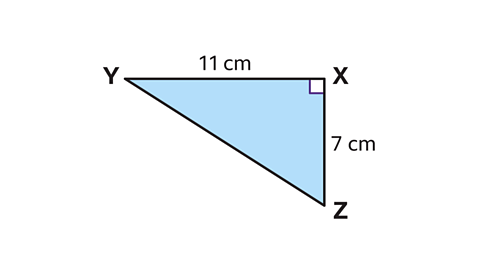
- Calculate the length of YZ.
Give the answer to one decimal place.
YZ = 13 cm to 1 d.p.
The shape is a right-angled triangle, and the two shorter sides are known.
The unknown side (YZ) is the hypotenuse.
Use Pythagoras’ theorem to find the value of YZ.
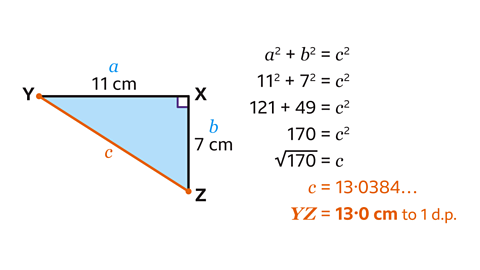
- Label the shorter sides of the triangle 𝑎 and 𝑏.
Remember that the hypotenuse, which is opposite the right-angle, should always be labelled c. The order of 𝑎 and 𝑏does not matter.
- Substitute the values into the formula 𝑎² + 𝑏² = 𝑐².
𝑎² = 11² and 𝑏² = 7².
- Calculate the value of the squares.
11² = 121 and 7² = 49.
Add the squares together to get 170. This is the value of 𝑐².
Find the square root to give 𝑐, the square root of 170.
This gives the answer of 𝑐 = 13.0384…
Therefore, when rounded to 1 decimal place, YZ = 13 cm.
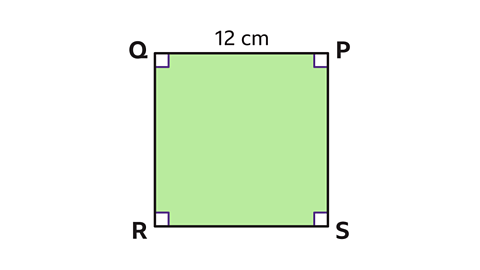
- A square PQRS has sides measuring 12 cm.
Calculate the length of PR.
Give the answer to one decimal place.
PR = 17 cm to 1 d.p.
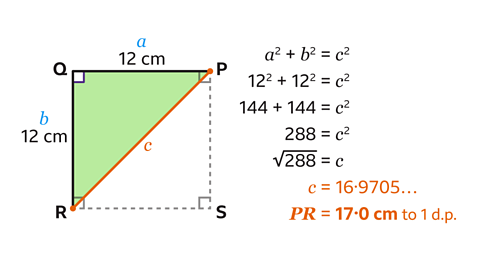
Adding the line PR splits the square into two congruent right-angled triangles. Two sides of the triangle are known.
- Use Pythagoras’ theorem to find the missing side.
Label the sides of the triangle a, b and c.
- Substitute the values into the formula 𝑎² + 𝑏² = 𝑐².
𝑎² = 12² and 𝑏² = 12².
- Calculate the value of the squares.
12² = 144
Add the squares together to get 288. This is the value of 𝑐².
Calculate the square root of 288. This gives the answer of c = 16.09705…, which is 17 cm to 1 d.p.
How to calculate a shorter side in a right-angled triangle
When the hypotenuse and one other side in a right-angled triangle are known, you can find the length of a shorter side by following these steps.
- First, label the sides of the triangle 𝑎, 𝑏 and 𝑐.
Remember that the hypotenuse, which is opposite the right-angle, should always be labelled 𝑐.
Substitute the values known into the formula 𝑎² + 𝑏² = 𝑐².
Calculate the squares to simplify the expression.
Subtract the smaller square from the larger square.
Take the square root of the value to find the length of the shorter side.
Follow the worked example below
GCSE exam-style questions
- Calculate the length of PQ.
Give the answer to one decimal place.
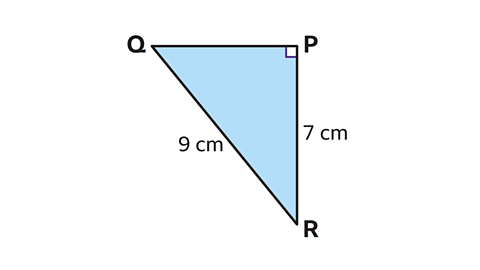
PQ = 5·7 cm to 1 d.p.
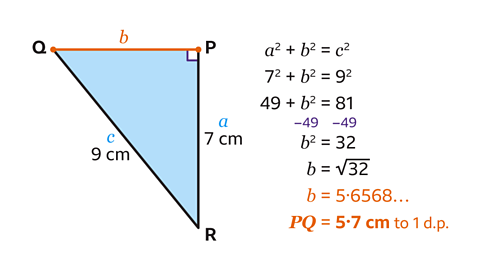
𝑎² = 7² and 𝑐² = 9².
Calculate the value of the squares.
7² = 49 and 9² = 81.
This gives the equation 49 + 𝑏² = 81.
Work out the value of 𝑏² by subtracting 49 from both sides of the equation. This gives 𝑏² = 32.
Find 𝑏 by calculating the square root of 32. This gives the answer of 𝑏 = 5·6568… or 5·7 cm to 1 decimal place.
- An isosceles triangle has a base of 6 cm and sides of 11 cm.
Use Pythagoras’ theorem to find the triangle’s height.
Give the answer to two decimal places.
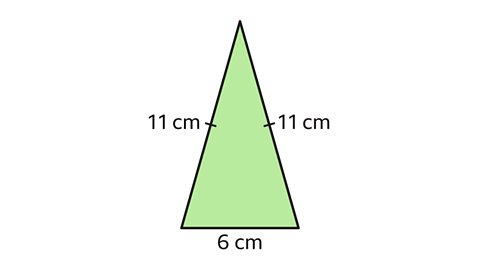
Height = 10·58 cm to 2 d.p.
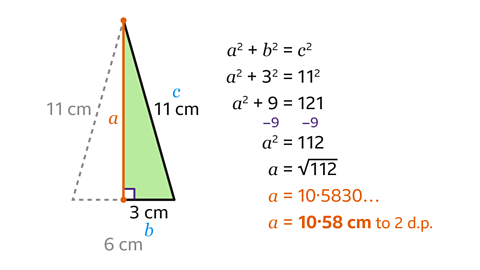
Adding the vertical height splits the isosceles triangle into two congruent right-angled triangles.
This line bisects the base so 6 ÷ 2 = 3.
- Label the sides of the triangle 𝑎, 𝑏 and 𝑐.
𝑏² = 3² and 𝑐² = 11².
- Calculate the value of the squares.
3² = 9 and 11² = 121.
This gives the equation 𝑎² + 9 = 121.
- Work out the value of 𝑎² by subtracting 9 from both sides of the equation.
This leads to the equation 𝑎² = 112.
- Find 𝑎 by calculating the square root of 112.
This gives the answer of 𝑎 = 10·5830… or 10·58 to 2 decimal places.
How to prove a triangle is right-angled
Pythagoras’ theorem is only true for right-angled triangles.
To test if a triangle is right-angled, all 3 sides must be known.
Substitute the values for 𝑎, 𝑏 and 𝑐 into the formula 𝑎² + 𝑏² = 𝑐².
If both sides of the formula are equal, then the formula is satisfyWhen a value makes an equation, inequality or statement true., and the triangle is therefore right-angled.
If the two sides are not equal, the triangle is not right-angled.
Follow the worked example below
GCSE exam-style questions
- Is triangle STU right-angled?
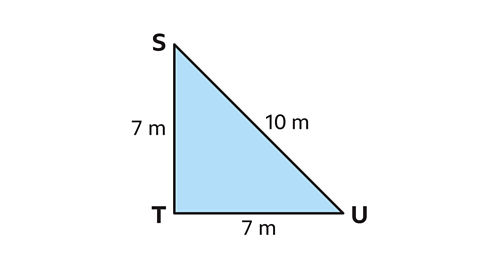
Triangle STU is not right-angled.
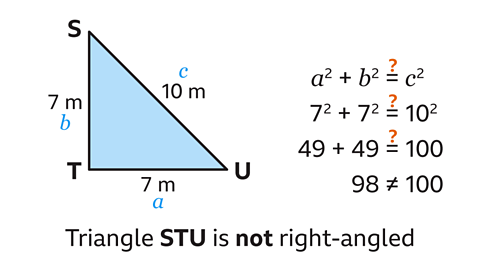
To prove if a triangle is right-angled, use Pythagoras’ theorem.
In triangle STU, 𝑎 = 7 m, 𝑏 = 7 m and 𝑐 = 10 m.
Calculate the value of the squares.
7² = 49 and 10² = 100.
This gives the calculation 49 + 49 = 100.
The left-hand side of the calculation, 49 + 49 = 98.
This does not equal the right-hand side of the calculation, 100.
Pythagoras’ theorem is not satisfied for this triangle, so the triangle is not right-angled.
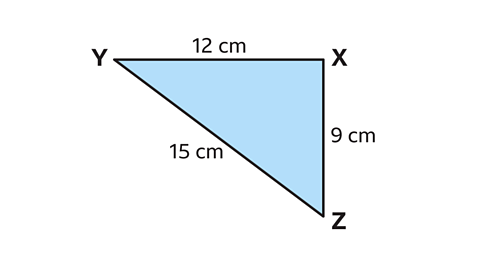
- Show that triangle XYZ is right-angled.
Triangle XYZ is right-angled.
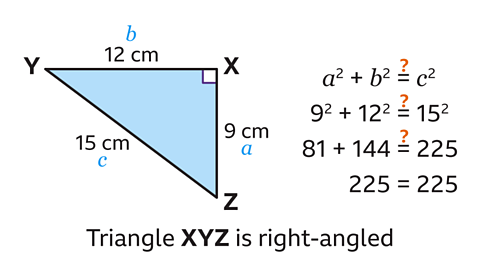
A triangle is right-angled if it satisfies Pythagoras’ theorem.
In triangle XYZ, 𝑎 = 9 cm, 𝑏 = 12 cm and 𝑐 = 15 cm.
Calculate the value of the squares.
9² = 81, 12² = 144 and 15² = 225.
This gives the calculation 81 + 144 = 225.
Both sides of the equation equal 225.
Pythagoras’ theorem is therefore satisfied for this triangle, so the triangle is right-angled.
Quiz – Pythagoras' theorem
Practise what you've learned about Pythagoras' theorem with this quiz.
Now you've revised Pythagoras' theorem, why not look at congruent and similar shapes?
More on Geometry and measure
Find out more by working through a topic
- count29 of 35

- count30 of 35

- count31 of 35
