Key points about right-angled trigonometry

Use trigonometry to find:
- a missing side in a right-angled triangle when another side and an angle are known.
- a missing angle in a right-angled triangle when two sides are known.
Use these three trigonometric ratioA part-to-part comparison. (or formulae):
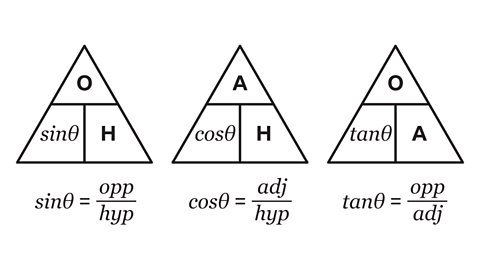
\( {sinθ} = \frac{opposite}{hypotenuse}\)
\( {cosθ} = \frac{adjacent}{hypotenuse}\)
\( {tanθ} = \frac{opposite}{adjacent}\)
In these formulae, the Greek letter θ (theta) is often used as a symbol for an unknown angle, and the formulae also include the names of the three sides of the triangle, often abbreviated to opp or O (opposite), adj or A (adjacent) and hyp or H (hypotenuse) .
The positions of the opposite and adjacent sides depend on the location of the angle, θ.
Make sure you are confident at substituting into and manipulating formulae.

Scientific calculators need to be used for trigonometry and should be in degrees mode.
Often there is a small D or DEG at the top of the calculator screen.
If not, go into the calculator settings to change the angle units to degrees.
How to find the length of a side with an unknown numerator
In a right-angled triangle, the hypotenuse is the longest side, opposite the right angle. The side opposite the given angle, θ, is called the opposite. The final side, next to the given angle, θ, is called the adjacent.
When finding a missing side in a right-angled triangle, another side and an angle must be known.

- Label the sides of the triangle with hypotenuse (hyp), opposite (opp) and adjacent (adj).
One of these sides will be known and the other will be unknown.
Use this to decide the correct trigonometric ratio to use.
- Substitute the values of the sides and the angle into the formula to create a trigonometric equation. The unknown side will be either the numeratorNumber written at the top of a fraction. The numerator is the number of parts used, eg for ⅓, the numerator is 1. or denominatorNumber written on the bottom of a fraction. The denominator is the number of equal parts, eg for ⅓, the denominator is 3. of the ratio.
- If the unknown side is the numerator in the equation, solve the equation by multiplying both sides by the denominator.
Follow the worked example below
GCSE exam-style questions
- Using trigonometry, find the length of 𝑥 to 1 decimal place.
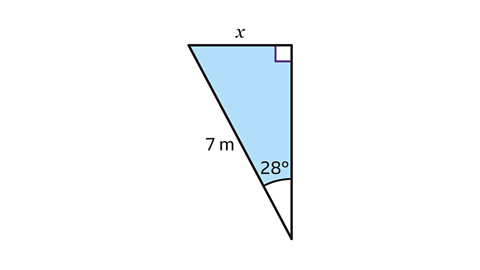
𝑥 = 3·3 m to 1 decimal place.
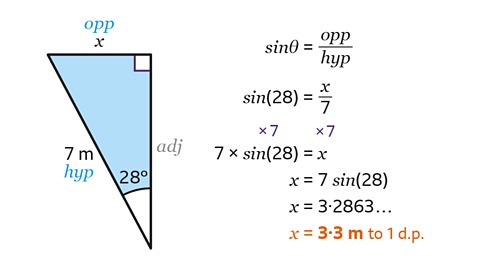
- Label the sides of the triangle.
- The hypotenuse (hyp) is the longest side and is opposite the right angle.
- The opposite side (opp) is the side opposite the given angle.
- The adjacent side (adj) is the final side next to the given angle.
- In this triangle the hypotenuse (hyp) is known and the opposite (opp) is the side to be calculated. The trigonometric ratio needed must contain the opposite and the hypotenuse.
Therefore, the correct formula to use is the sine ratio, sinθ = opp ÷ hyp.
Write down the formula sinθ = opp ÷ hyp.
Substitute the values of θ, opp and hyp into the formula to form an equation.
Here θ = 28°, the opposite should be substituted with 𝑥, and the hypotenuse is 7.This gives sin(28) = 𝑥 ÷ 7.
Rearrange the equation to make 𝑥 the subject.
Find the value of 𝑥 by multiplying both sides of the equation by 7.
This gives 7 × sin(28) = 𝑥, or written without the multiplication sign 𝑥 = 7sin(28).
- Type 7sin(28) into a scientific calculator.
This gives 𝑥 = 3·2863…
Rounded to 1 decimal place, 𝑥 = 3·3 m.
- Using trigonometry, find the length of AC to 1 decimal place.
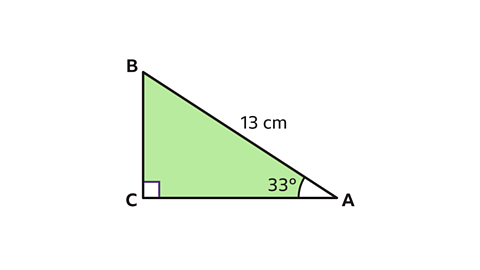
AC = 10·9 cm to 1 decimal place.
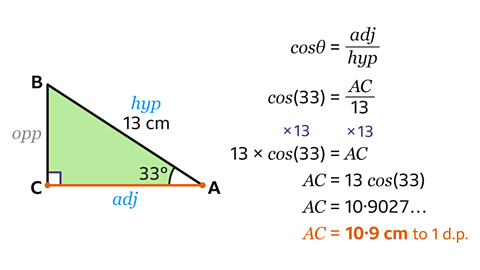
- Label the sides of the triangle.
In this triangle the hypotenuse (hyp) is known and the adjacent (adj) is the side to be calculated, AC.
The correct formula to use is the cosine ratio, cosθ = adj ÷ hyp.
Write down the formula cosθ = adj ÷ hyp.
Substitute the values of θ, adj and hyp into the formula to form an equation.
Here θ = 33°, the adjacent should be substituted with AC, and the hypotenuse is 13.
This gives cos(33) = AC ÷ 13.
Rearrange the equation to make AC the subject.
Multiply both sides of the equation by 13, to find the value of AC.
This gives 13 × cos(33) = AC, or written without the multiplication sign AC = 13cos(33).
- Type 13cos(33) into a scientific calculator.
This gives AC = 10·9027…
Rounded to 1 decimal place, AC = 10·9 cm.
How to find the length of a side with an unknown denominator
If the unknown side is the denominator in the equation, more steps are required to solve the equation.
First multiply both sides by the unknown side (𝑥).
To make 𝑥 the subject of the equation, divide both sides by the trigonometric function of the given angle.
Follow the worked example below
GCSE exam-style questions
- Use trigonometry to find the length of 𝑥 to 1 decimal place.
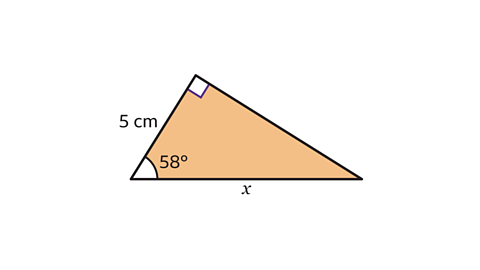
𝑥 = 9·4 cm to 1 decimal place.
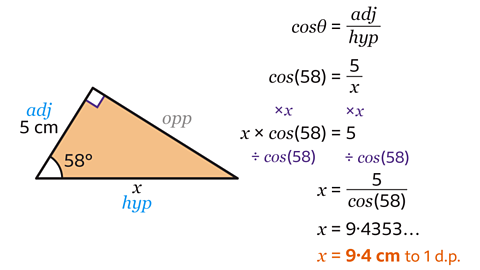
- Label the sides of the triangle.
In this triangle the adjacent (adj) is known and the hypotenuse (hyp) is the side that needs to be calculated.
The trigonometric ratio needed must contain the adjacent and the hypotenuse.
Therefore, the correct formula to use is the cosine ratio, cosθ = adj ÷ hyp.
Write down the formula cosθ = adj ÷ hyp.
Substitute the values of θ, adj and hyp into the formula to form an equation.
Here θ = 58°, the adjacent is 5, and the hypotenuse should be substituted with 𝑥.
This gives cos(58) = 5 ÷ 𝑥.
Rearrange the equation, to make 𝑥 the subject.
- First multiply both sides of the equation by 𝑥. This gives 𝑥 × cos(58) = 5.
- Divide both sides of the equation by cos(58). This gives 𝑥 = 5 ÷ cos(58).
Type 5 ÷ cos(58) into a scientific calculator. This gives 𝑥 = 9·4353…
Rounded to 1 decimal place, 𝑥 = 9·4 cm.
- Use trigonometry to find the length of YZ to 1 decimal place.
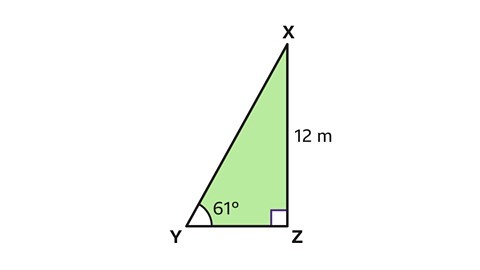
YZ = 6·7 m to 1 decimal place.
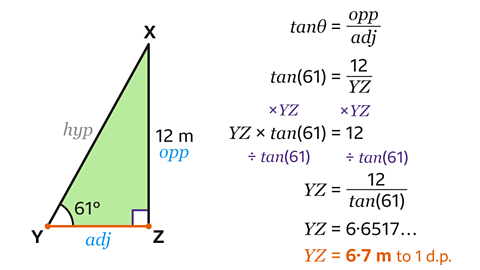
- Label the sides of the triangle.
In this triangle, the opposite (opp) is known and the adjacent (adj) is the side to be calculated. The trigonometric ratio needed must contain the opposite and the adjacent.
Therefore, the correct formula to use is the tangent ratio, tanθ = opp ÷ adj.
Write down the formula tanθ = opp ÷ adj.
Substitute the values of θ, opp and adj into the formula to form an equation.
Here θ = 61°, the opposite is 12, and the adjacent should be substituted with YZ.
This gives tan(61) = 12 ÷ YZ.
Rearrange the equation to make YZ the subject.
Multiply both sides of the equation by YZ.
This gives YZ × tan(61) = 12.
- Divide both sides of the equation by tan(61).
This gives YZ = 12 ÷ tan(61).
- Type 12 ÷ tan(61) into a scientific calculator.
This gives YZ = 6·6517…
Rounded to 1 decimal place, YZ = 6·7 m.
How to use trigonometry to calculate an unknown angle
When finding a missing angle, θ, in a right-angled triangle, the lengths of two sides must be known.
- Label the sides of the triangle with hypotenuse (hyp), opposite (opp), and adjacent (adj).
Two of these sides will be known.
- Use this to decide which is the correct trigonometric ratio to use.
- Substitute the values of the sides into the formula to create a trigonometric equation.
To work out the angle, θ, use the inverseThe opposite of a mathematical process. For example, the inverse of × 5 is ÷ 5. The inverse process undoes the original process. function.
For example, the inverse function of sine, sin⁻¹, can usually be written into a scientific calculator by pressing 'Shift' or ‘2ndF’ then 'sin'.
This can be done in a similar way for cos⁻¹ and tan⁻¹.
Follow the worked example below
GCSE exam-style questions
- Use trigonometry to find the size of θ.
Give the answer to 1 decimal place.
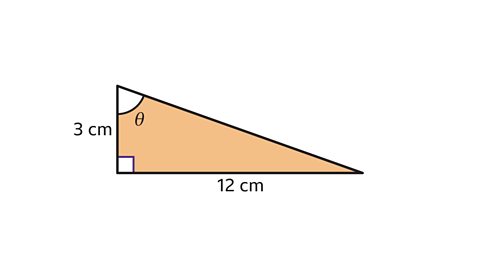
θ = 76·0° to 1 decimal place.
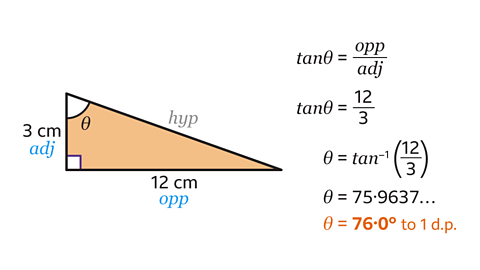
- Label the sides of the triangle.
In this triangle the opposite (opp) and the adjacent (adj) sides are known.
The trigonometric ratio needed must contain the opposite and the adjacent.
Therefore, the correct formula to use is the tangent ratio, tanθ = opp ÷ adj.
- Substitute the values of opp, adj and θ into the formula to form an equation.
Here the opposite is 12, the adjacent is 3 and the angle should be substituted with θ.
This gives tanθ = 12 ÷ 3.
- Work out the angle, θ, by using the inverse function of tangent.
θ = tan⁻¹ (12 ÷ 3).
- Write tan⁻¹ on a scientific calculator, by pressing 'Shift' then 'tan'.
Then type 12 ÷ 3. Remember to close the brackets.
This gives θ = 75·9637…
Rounded to 1 decimal place, θ = 76·0°.
- Use trigonometry to find the size of angle CAB.
Give the answer to 1 decimal place.
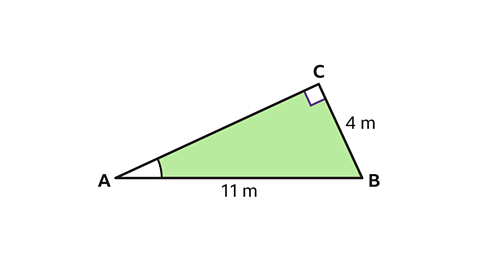
Angle CAB = 21.3° to 1 decimal place.
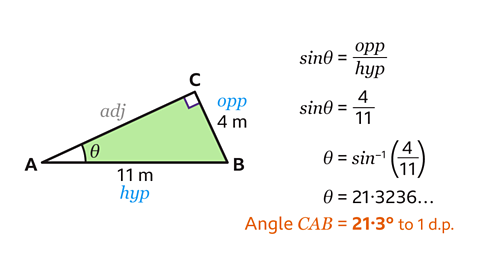
- Name angle CAB.
In this triangle, both the opposite (opp) and the hypotenuse (hyp) sides are known.
The trigonometric ratio needed must contain the opposite and the hypotenuse.
The correct formula to use is the sine ratio, sinθ = opp ÷ hyp.
- Substitute the values of opp, hyp and θ into the formula to form an equation.
Here the opposite is 4, the hypotenuse is 11 and the angle should be substituted with θ.
This gives sinθ = 4 ÷ 11.
- Work out the angle, θ, by using the inverse function of sine.
θ = sin⁻¹ (4 ÷ 11).
- Write sin⁻¹ on a scientific calculator, by pressing 'Shift' then 'sin'.
Then type 4 ÷ 11. Remember to close the brackets.
This gives θ = 21·3236…
Rounded to 1 decimal place, angle CAB = 21·3°.
Check your understanding
Quiz – Right-angled trigonometry
Practise what you've learned about right-angled trigonometry with this quiz.
Now you've revised right-angled trigonometry, why not check out reflection?
More on Geometry and measure
Find out more by working through a topic
- count30 of 35

- count31 of 35

- count32 of 35

- count33 of 35
