Key points about reflection

A reflectionA transformation of a shape which results in a mirror image of the shape with respect to a line. is one of the four types of transformations. A shape can be reflected in a line to create a congruentShapes that are the same shape and size, they are identical. image of the shape.
Each vertexThe point at which two or more lines cross. The corner of a shape. The plural form is vertices. on the original shape is the same perpendicularPerpendicular lines are at 90° (right-angles) to each other. distance from the line of reflection, or mirror line, to its corresponding vertex on the image.
Knowing the distance between corresponding points and the mirror line is equal can help find the position of the mirror line when given an objectThe starting shape prior to a transformation. and its image.
When reflecting shapes in non-vertical lines, rotating the paper to make the line of reflection vertical can help to visualise the problem.
Make sure you have a good understanding of plotting coordinates and the equation of a straight line.
How to reflect shapes in horizontal and vertical lines
Reflections can either be shown on a square grid or on a set of axes.
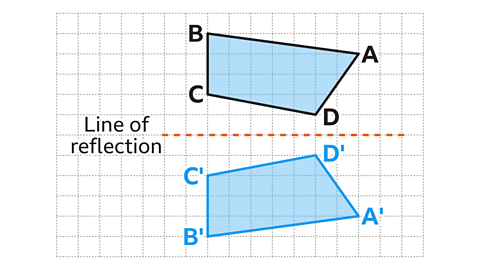
Shape 𝑃'𝑄'𝑅'𝑆' in the image is a reflection of the shape 𝑃𝑄𝑅𝑆.
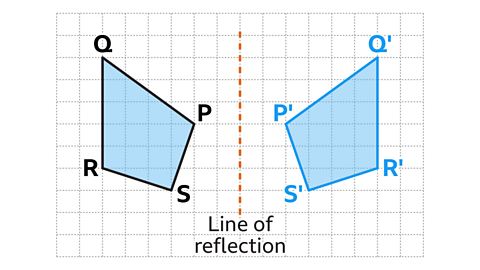
Watch the example below
Read the steps below to see the full method outlined.
To work out the position of the image, with respect to a mirror line, after a reflection:
Pick a vertex on the shape (object).
Work out the perpendicular distance to the line of reflection by counting the number of squares on the grid.
Count the same perpendicular distance from the line of reflection to the opposite side of the line of reflection. This will be the reflected vertex.
Repeat the process for additional vertices.
GCSE exam-style questions
- Triangle 𝑋𝑌𝑍 is reflected in the vertical line.
Work out the position of the image using paper, a pencil and a ruler.
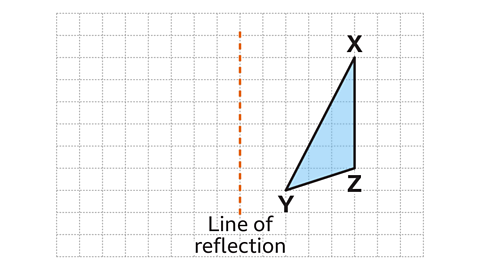
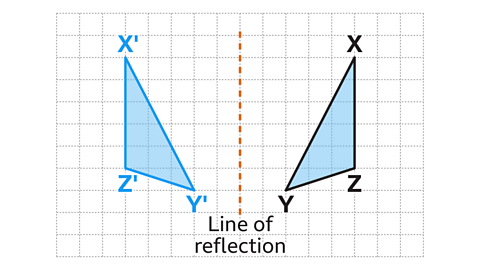
Vertex 𝑋 is five squares to the right of the line of reflection. The corresponding vertex 𝑋' is five squares to the left of the line of reflection.
Vertex 𝑌 is two squares to the right of the line of reflection. The corresponding vertex 𝑌' is two squares to the left of the line of reflection.
Vertex 𝑍 is five squares to the right of the line of reflection. The corresponding vertex 𝑍' is five squares to the left of the line of reflection.
- Quadrilateral 𝐴𝐵𝐶𝐷 is reflected in the horizontal line.
Work out the position of the image using paper, a pencil and a ruler.
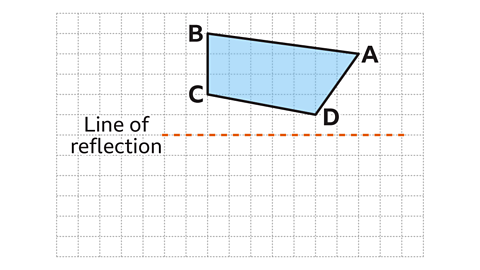
Vertex 𝐴 is four squares above the line of reflection. The corresponding vertex 𝐴' is four squares below the line of reflection.
Vertex 𝐵 is five squares above the line of reflection. The corresponding vertex 𝐵' is five squares below the line of reflection.
Vertex 𝐶 is two squares above the line of reflection. The corresponding vertex 𝐶' is two squares below the line of reflection.
Vertex 𝐷 is one square above the line of reflection. The corresponding vertex 𝐷' is one square below the line of reflection.
How to reflect shapes in diagonal lines
To reflect a shape in a diagonalA line joining two non-adjacent vertices (corners) of a polygon. line, a small change to the method used for reflecting shapes in horizontal and vertical lines is needed.
Since the line of reflection is a diagonal, the perpendicular distance is also diagonal.
Instead, count the diagonal distances from a point to the mirror line.
Pick a vertex on the object shape.
Work out the perpendicular distance to the line of reflection. This is done by drawing a line from the vertex which passes through the diagonal of each square on the grid, until the line of reflection is reached.
Count the same perpendicular distance from the line of reflection to the opposite side of the line of reflection. This will be the position of the reflected vertex.
Repeat the process for additional vertices.
Follow the worked example below
GCSE exam-style questions
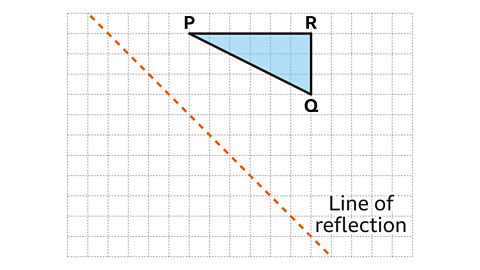
- Triangle 𝑃𝑄𝑅 is reflected in the diagonal line of reflection.
Work out the position of the image using paper, a pencil and ruler.
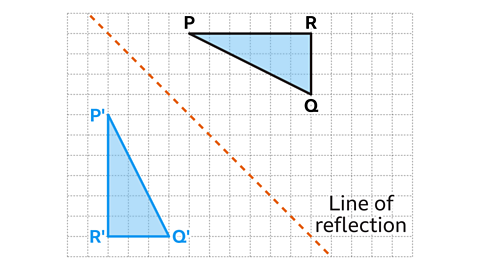
Vertex 𝑃 is two diagonals of a square to the line of reflection. The corresponding vertex 𝑃' passes through two diagonals from the line of reflection on the opposite side.
Vertex 𝑄 is three and a half diagonals of a square to the line of reflection. The corresponding vertex 𝑄' passes through three and a half diagonals from the line of reflection on the opposite side.
Vertex 𝑅 is five diagonals of a square to the line of reflection. The corresponding vertex 𝑅' passes through five diagonals from the line of reflection on the opposite side.
- Quadrilateral 𝐴𝐵𝐶𝐷 is reflected in the diagonal line of reflection.
Work out the position of the image using paper, a pencil and a ruler.
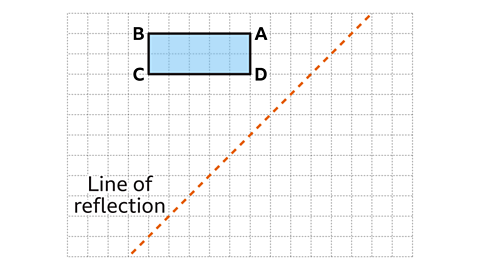
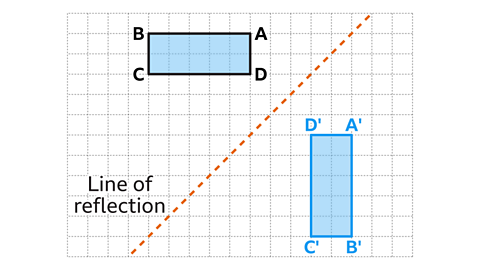
Vertex 𝐴 is two and a half diagonals of a square to the line of reflection. The corresponding vertex 𝐴' passes through two and a half diagonals from the line of reflection on the opposite side.
Vertex 𝐵 is five diagonals of a square to the line of reflection. The corresponding vertex 𝐵' passes through five diagonals from the line of reflection on the opposite side.
Vertex 𝐶 is four diagonals of a square to the line of reflection. The corresponding vertex 𝐶' passes through four diagonals from the line of reflection on the opposite side.
Vertex 𝐷 is one and a half diagonals of a square to the line of reflection. The corresponding vertex 𝐷' passes through one and a half diagonals from the line of reflection on the opposite side.
How to reflect shapes on a set of axes
Check your understanding
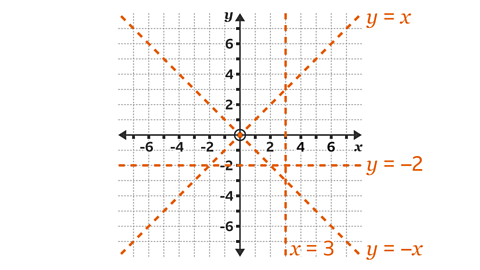
To reflect a shape on a set on axes, apply the method of counting the squares.
The lines of reflection on a set of axes can either be:
- vertical, eg 𝑥 = 3
- horizonal, eg 𝑦 = – 2
- diagonal, eg 𝑦 = – 𝑥
To describe a reflection, name the equation of the line that the shape has been reflected in, such as 'shape 𝐴 is a reflection in the line 𝑥 = 3'.


When using coordinates:
the first number represents the horizontal position (along the 𝑥-axis)
the second number represents the vertical position (along the 𝑦-axis)
Follow the worked examples below
GCSE exam-style questions
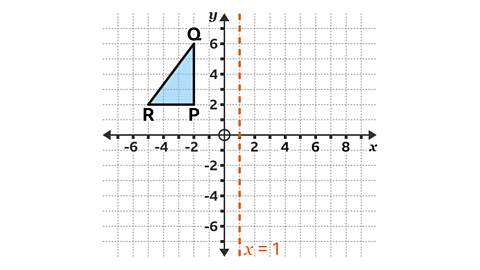
- Triangle 𝑃𝑄𝑅 is reflected in the line 𝑥 = 1.
What are the coordinates of the image of the reflected shape?
The coordinates are (4, 2), (4, 6) and (7, 2).
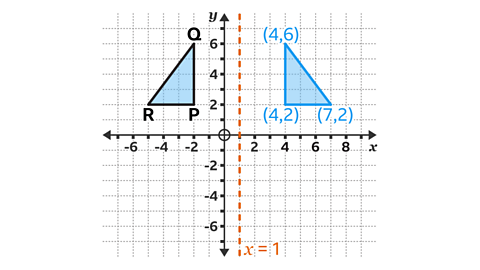
Vertex 𝑃 is three squares to the left of the line of reflection. The corresponding vertex is three squares to the right of the line of reflection. It has the coordinates (4, 2).
Vertex 𝑄 is also three squares to the left of the line of reflection. The corresponding vertex is three squares to the right of the line of reflection. It has the coordinates (4, 6).
Vertex 𝑅 is six squares to the left of the line of reflection. The corresponding vertex is six squares to the right of the line of reflection. It has the coordinates (7, 2).
- Shape 𝐵 is a reflection of shape 𝐴.
What is the equation of the line that the shape has been reflected in?
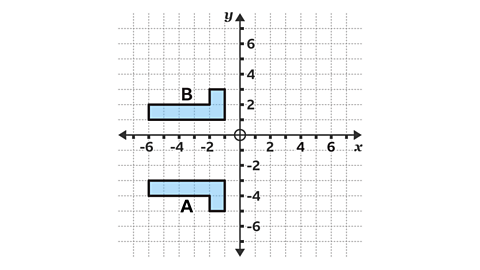
The equation of the line is 𝑦 = – 1.
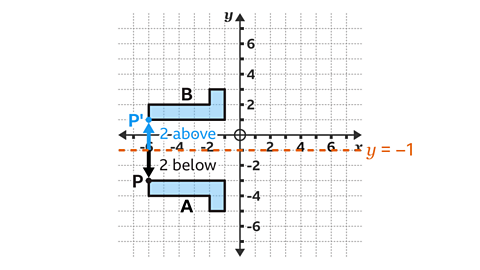
This is a horizontal line that maintains an equal perpendicular distance between the object, line of reflection and image.
For example, the vertex marked as 𝑃, on shape 𝐴, is two squares below the line of reflection. Therefore, the corresponding vertex, 𝑃' must be two squares above the line of reflection.
- Shape 𝐷 is a reflection of shape 𝐶.
What is the equation of the line that the shape has been reflected in?
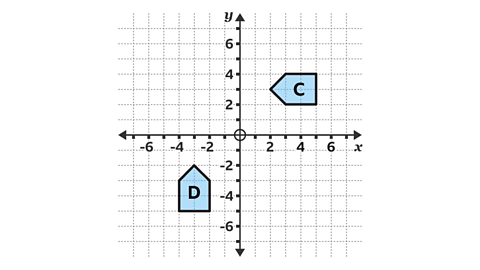
The equation of the line is 𝑦 = – 𝑥.
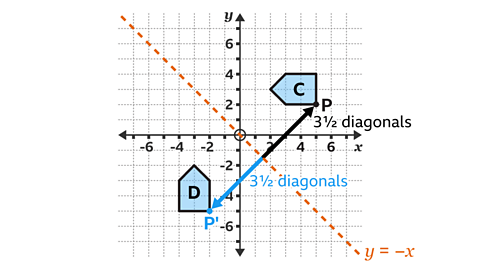
This is a diagonal line that maintains an equal perpendicular distance between the object, line of reflection and image.
For example, the vertex marked as 𝑃, on shape 𝐶, is three and a half diagonals of a square to the line of reflection. Therefore, the corresponding vertex, 𝑃' must be three and a half diagonals the opposite side of the line of reflection.
- Reflect triangle 𝐴 in the line 𝑦 = – 2 onto triangle 𝐵.
What are the coordinates of triangle 𝐵?
Reflect triangle 𝐴 in the line 𝑦 = – 𝑥 onto triangle 𝐶.
What are the coordinates of triangle 𝐶?
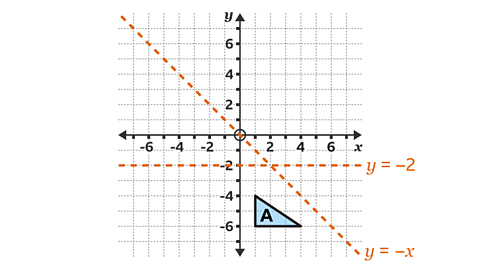
Triangle 𝐵 has coordinates (1, 0), (1, 2) and (4, 2).
Triangle 𝐶 has coordinates (4, – 1), (6, – 1) and (6, – 4).
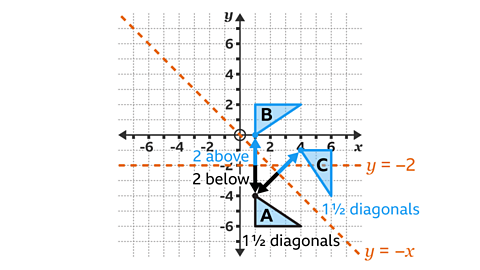
The vertex at (1, – 4) on triangle 𝐴 is two squares below the line of reflection. The corresponding vertex on triangle 𝐵 is two squares above the line of reflection. It has the coordinates (1, 0). This process can be repeated for the other two vertices.
The vertex (1, – 4) on triangle 𝐴 is one and a half diagonals to the line of reflection. The corresponding vertex on triangle 𝐶 is one and a half diagonals on the other side of the line of reflection. It has the coordinates (4, – 1). This process can be repeated for the other two vertices.
Reflection – Interactive activity
This interactive activity will help you understand how to reflect a shape in a given line on a set of axes.
Quiz – Reflection
Practise what you've learned about reflection with this quiz.
Now you've revised reflection, why not look at higher – similarity in 2D and 3D shapes?
More on Geometry and measure
Find out more by working through a topic
- count20 of 35

- count21 of 35

- count22 of 35

- count23 of 35
