Key points about negative enlargements
An A transformation of a shape which results in a shape increasing or decreasing in size. produced by a negative scale factor is on the opposite side of the A point which defines the position of an enlarged shape. to the original shape.
- For example, a A number by which an amount or measurement is multiplied to enlarge or reduce it. of −2 produces the same size shape as a scale factor of 2 but its position and orientation are different.
Make sure you are confident in working with enlargements on a set of axes, when looking at negative enlargements.
Check your understanding
Enlarging with a negative scale factor and a centre of enlargement
To work out the position of the image after a negative enlargement:
Pick a vertex on the shape (object).
Count the distance between the centre of enlargement and the vertex. This can be separated into horizontal and vertical A change in position of a shape relative to its start point..
Multiply these displacements by the scale factor.
Using these values, count in the opposite direction from the centre of enlargement to find the position of the corresponding vertex.
Repeat the process for additional vertices.
Check the answer by drawing lines through A pair of matching vertices or edges on similar shapes. points on both the object and the image. If done correctly, these will meet at the centre of A transformation of a shape which results in a shape increasing or decreasing in size..
When counting in the opposite direction, the orientation of the image is rotated through 180°.
Follow the worked example
GCSE exam-style questions
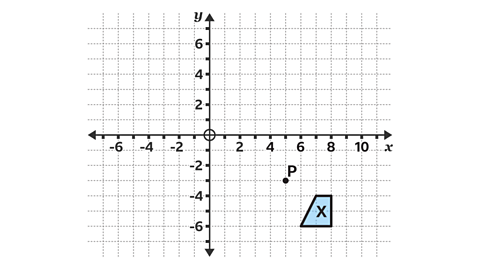
- Enlarge shape X by a scale factor of −3.
Use point P with the coordinates of (5, −3) as the centre of enlargement.
Work out the position of the enlargement using paper, a pencil and ruler.
Label your enlargement Y.
Shape Y has vertices at (2, 6), (−4, 6), (−4, 0) and (−1, 0).
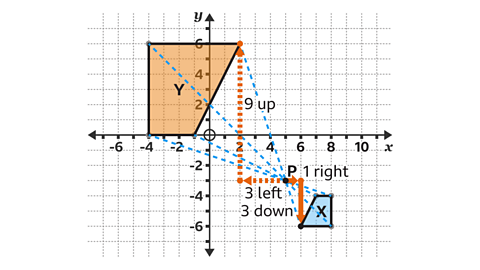
- Calculate the position of each new vertex.
For example, the vertex at (6, −6) is one square to the right and three squares below the centre of enlargement.
- Multiply this displacement by the scale factor of −3.
1 × −3 = −3 and 3 × − 3 = −9
The negative numbers serve as a reminder to count in the opposite direction.
The corresponding point needs to be three squares to the left and nine squares above the centre of enlargement.
The corresponding point has the co-ordinate (2, 6).
Repeat for the other three vertices.
Check the position of the enlargement by drawing lines through pairs of corresponding points.
These dashed lines all meet at the centre of enlargement, point P.
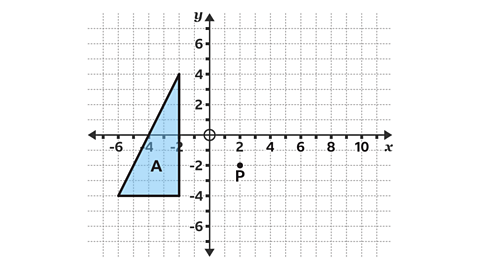
- Enlarge shape A by a scale factor −½.
Use point P with the coordinates of (2, −2) as the centre of enlargement.
Work out the position of the enlargement using paper, a pencil and ruler.
Label your enlargement B.
Shape B has vertices at (4, −5), (6, −1), and (4, −1).
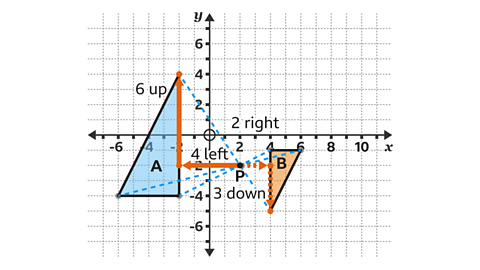
- Calculate the position of each new vertex.
For example, the vertex at (−2, 4) is four squares to the left and six squares above the centre of enlargement.
- Multiply this displacement by the scale factor of −½.
4 × −½ = −2 and 6 × −½ = −3
The negative numbers serve as a reminder to count in the opposite direction.
The corresponding point needs to be two squares to the right and three squares below the centre of enlargement.
The corresponding point has the co-ordinate (4, −5).
3 Repeat for the other two vertices.
- Check the position of the enlargement by drawing lines through pairs of corresponding points.
These dashed lines all meet at the centre of enlargement, point P.
How to describe an enlargement using a negative scale factor
The same method for finding the centre of enlargement for a positive scale factor is also used to find the centre of enlargement for a negative scale factor.
The lines which pass through corresponding points on the object and image When lines cross or overlap. at the centre of enlargement.
The transformation is fully described by specifying the type of transformation, in this case an enlargement, and calculating the correct negative scale factor and centre of enlargement.
Follow the worked example
GCSE exam-style questions
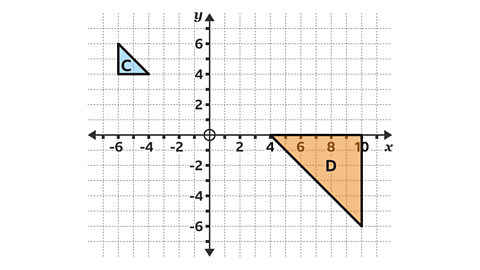
- Triangle D is a transformation of triangle C.
Describe the transformation fully.
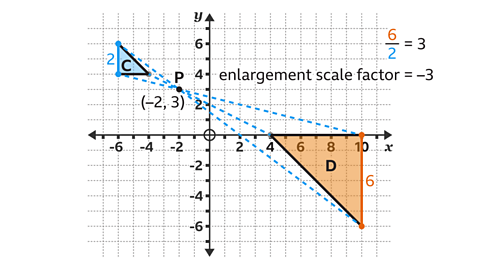
Triangle D is an enlargement of triangle C, by a scale factor of −3 and the centre of enlargement at (−2, 3).
Triangle D is an enlargement of triangle C, as the size of the shape has changed.
Draw lines through corresponding points on the object and image, to find the centre of enlargement. The lines converge at point P at (−2, 3).
Calculate the scale factor by dividing a pair of corresponding sides.
Triangle D has a vertical side with length 6 squares.
Triangle C has a corresponding vertical side with length 2 squares.
⁶⁄₂ = 3
- Make the scale factor negative, as the produced enlargement is on the opposite side of the centre of enlargement.
Therefore, triangle D is an enlargement of triangle C by a scale factor of −3.
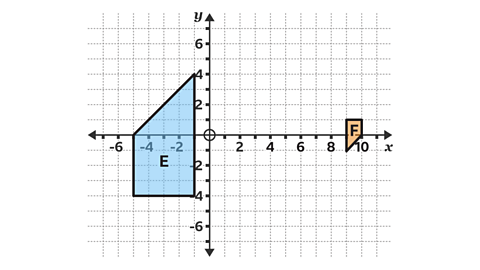
- Shape F is a transformation of shape E.
Describe the transformation fully.
Shape F is an enlargement of shape E by a scale factor of −¼, with the centre of enlargement at (7, 0).
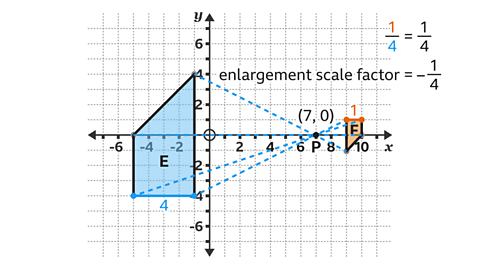
Shape F is an enlargement of shape E, as the size of the shape has changed.
- Draw lines through corresponding points on the object and image, to find the centre of enlargement. The lines converge at point P.
The centre of enlargement is at (7, 0).
- Divide a pair of corresponding sides, to calculate the scale factor.
Shape F has a horizontal side with length 1 square.
Shape E has a corresponding horizontal side with length 4 squares.
1 ÷ 4 = ¼
- Make the scale factor negative, as the produced enlargement is on the opposite side of the centre of enlargement.
Therefore, shape F is an enlargement of shape E by a scale factor of −¼.
Quiz – Negative enlargements
Practise what you've learned about negative enlargements with this quiz.
Now you've revised negative enlargements, why not take a look at the sine rule?
More on Geometry and measure
Find out more by working through a topic
- count25 of 30
- count26 of 30
- count27 of 30
