Key points about enlargement

An enlargementA transformation of a shape which results in a shape increasing or decreasing in size. is one of the four types of transformationA transformation changes the position or size of a shape..
An enlargement increases or decreases the size of a shape. The new shape is a similarOne shape is an enlargement of another. The angles in each shape are the same, and the side lengths are in the same proportion. shape.
The increase in size from one shape to another similar shape is called a scale factorThe ratio between corresponding sides in an enlargement..
The position of the enlarged shape is determined by a point, called the centre of enlargementA point which defines the position of an enlarged shape..
Make sure you're confident at working with axes and plotting coordinates and have a good understanding of similar shapes.
Check your understanding
What is a scale factor?
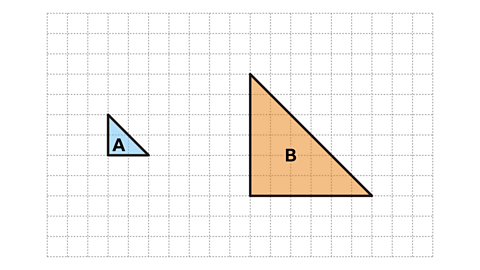
When a shape is enlarged, the length of each side is multiplied by the same value.
This is called the scale factor.
To make a shape four times bigger, the lengths of all sides are multiplied by four. Since the new shape is similar, all of the angles in the enlarged shape are the same size. The shape has been enlarged by a scale factor of 4.
When given two shapes, calculate the scale factor by dividing the lengths of corresponding sides of each shape.
A scale factor, greater than one, produces a larger shape.
A scale factor between zero and one results in a smaller shape.

Follow the worked example below
GCSE exam-style questions
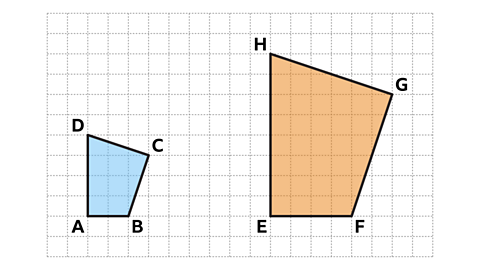
- Shape 𝐸𝐹𝐺𝐻 is an enlargement of shape 𝐴𝐵𝐶𝐷.
What is the scale factor of the enlargement?
Scale factor 2
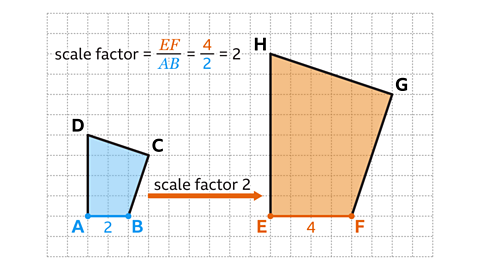
Shape 𝐸𝐹𝐺𝐻 is larger than shape 𝐴𝐵𝐶𝐷. The scale factor for a larger shape will be greater than one.
Calculate the scale factor by dividing a pair of corresponding sides.
In these shapes 𝐴𝐵 and 𝐸𝐹 are two corresponding horizontal sides.
𝐴𝐵 has a length of two squares and 𝐸𝐹 has a length of four squares.
Scale factor =\(\frac{ 𝐸𝐹}{𝐴𝐵} \) = \(\frac{4}{2} \) = 2.
Therefore, shape 𝐸𝐹𝐺𝐻 is an enlargement of shape 𝐴𝐵𝐶𝐷 by a scale factor of 2.
- Triangle 𝑋 is an enlargement of triangle 𝑌.
What is the scale factor of the enlargement?
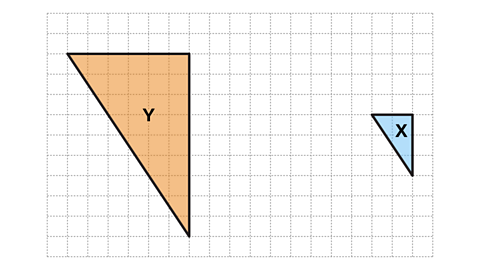
Scale factor ⅓
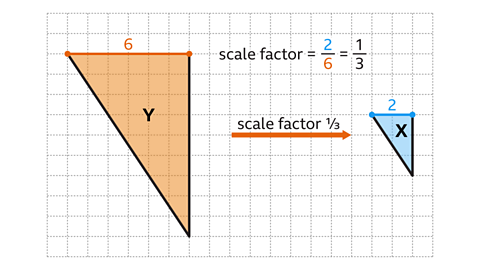
Triangle 𝑋 is smaller than triangle 𝑌. The scale factor for a smaller shape will be between zero and one.
Calculate the scale factor by dividing a pair of corresponding sides.
Triangle 𝑌 has a horizontal side with length six squares. Triangle 𝑋 has a corresponding horizontal side with length two squares.
Scale factor = ²⁄₆, which can be simplified to ⅓.
Therefore, triangle 𝑋 is an enlargement of triangle 𝑌 by a scale factor of ⅓.
Enlarging with a positive scale factor and a centre of enlargement
When using a centre of enlargementA point which defines the position of an enlarged shape., the final position of the enlarged shape can be determined. Shapes can be enlarged on sets of axes.
Check your answer by drawing lines through corresponding pointsWhen a shape is transformed (for example, by translation, rotation, reflection, or enlargement), each point on the original shape matches up with a point on the new shape. These matching points show how the position of the original shape relates to the transformed shape. on the object and image. If done correctly, these will meet at the centre of enlargementA point which defines the position of an enlarged shape..
Watch the example of using a centre of enlargement to enlarge a shape on a set of axes.
Read the steps below to see the full method outlined.
To work out the position of the image after enlargement:
Pick out a vertex on the shape (object).
Count the distance between the centre of enlargement and the vertex. This can be separated into horizontal and vertical displacements.
Multiply these displacements by the scale factor.
Using these values, count from the centre of enlargement to find the position of the corresponding vertex.
Repeat the process for additional vertices.
GCSE exam-style questions
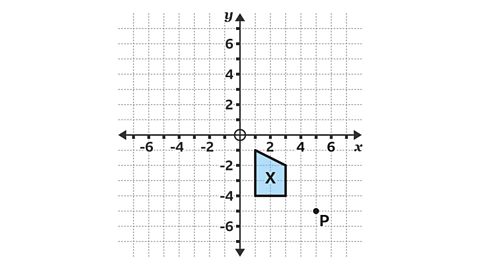
- Enlarge shape 𝑋 by a scale factor 2.
Use point 𝑃 with the coordinates of (5, – 5) as the centre of enlargement.
Check the position of the enlargement using paper, a pencil and ruler.
Label your enlargement 𝑌.
Shape 𝑌 has vertices at (1, – 3), (1, 1), ( – 3, 3) and
( – 3, – 3).
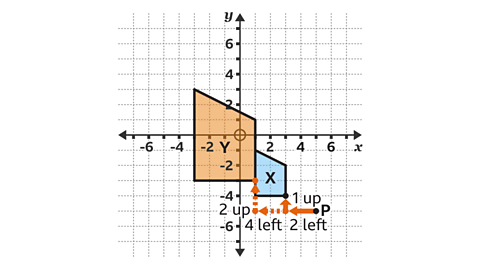
The position of each new vertex can be calculated.
For example, the vertex at ( 3, – 4) is two squares to the left and one square above the centre of enlargement.
- Multiply this displacement by the scale factor of 2.
2 × 2 = 4 and 1 × 2 = 2.
The corresponding point needs to be four squares to the left and two squares above the centre of enlargement.
The corresponding point has the coordinates (1, – 3).
Repeat this for the other three vertices.
Check the position of enlargement by drawing dashed lines through pairs of corresponding points.
If done correctly, the dashed lines will all meet at the centre of enlargement, point 𝑃.
- Enlarge triangle 𝐶 by a scale factor ½.
Use point 𝑃 with the coordinates of (2, 5) as the centre of enlargement.
Check the position of the enlargement using paper, a pencil and ruler.
Shape 𝐷 has vertices at (3, 3), ( – 2, 3) and ( – 1, – 1).
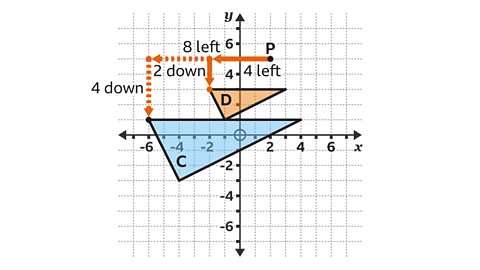
- Calculate the position of each new vertex.
For example, the vertex at ( – 6, 1) is eight squares to the left and four squares below the centre of enlargement.
- Multiply this displacement, by scale factor of ½.
½ × 8 = 4 and ½ × 4 = 2.
The corresponding point needs to be four squares to the left and two squares below the centre of enlargement.
The corresponding point has the coordinates ( – 2, 3).
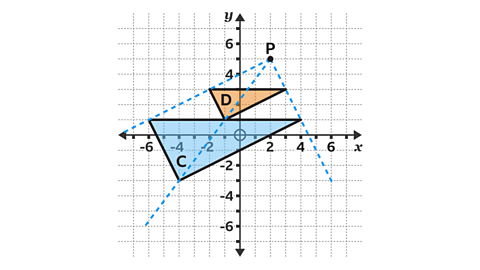
Repeat for the other two vertices.
Check the position of enlargement by drawing dashed lines through pairs of corresponding points.
If done correctly, the dashed line will all meet at the centre of enlargement, point 𝑃.
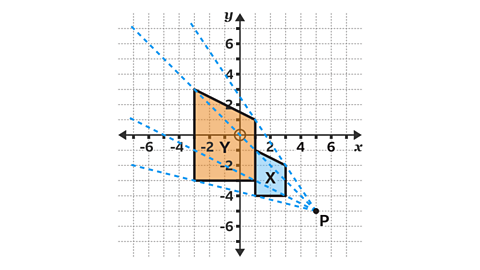
How do you find the centre of enlargement?
Find the centre of enlargement by using the method for checking the position of an enlarged shape.
The lines which pass through corresponding points on the object and image convergeLines that meet at a point. at the centre of enlargement.
Describe the transformation fully by stating the type of transformation, in this case an enlargement, and calculating the correct scale factor and centre of enlargement.
Follow the worked example below
GCSE exam-style questions
- Rectangle 𝐷 is a transformation of rectangle 𝐶.
Describe the transformation fully.
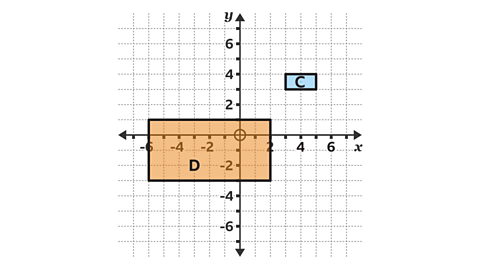
Rectangle 𝐷 is an enlargement of rectangle 𝐶, by a scale factor of 4, with the centre of enlargement at (6, 5).
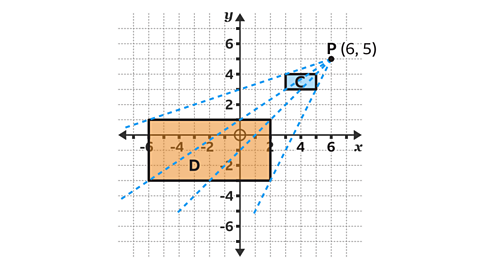
- Find the centre of enlargement by drawing lines through corresponding points on the object and image.
The lines converge at point 𝑃 with coordinates (6, 5).
Rectangle 𝐷 is larger than rectangle 𝐶.
The scale factor for a larger shape will be greater than one.
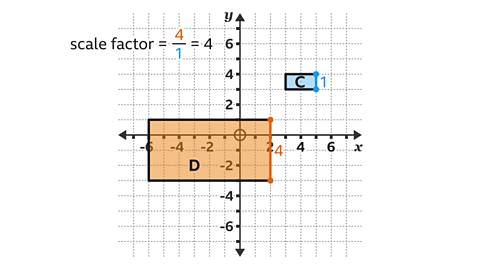
- Calculate the scale factor by dividing a pair of corresponding sides.
Rectangle 𝐶 has a vertical side with a length of 1 square.
Rectangle 𝐷 has a corresponding vertical side with a length of four squares.
Scale factor = \(\frac{4}{1}\) = 4.
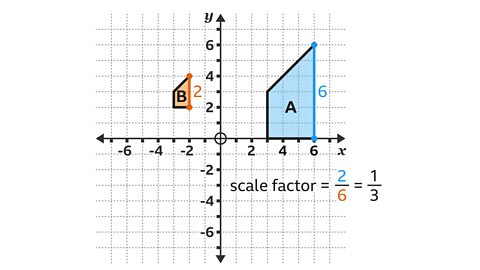
- Shape 𝐵 is a transformation of shape 𝐴
Describe the transformation fully.
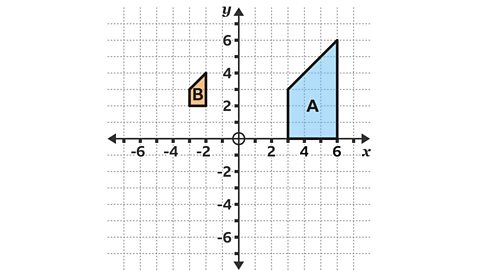
Shape 𝐵 is an enlargement of shape 𝐴 by a scale factor of ⅓, with the centre of enlargement at ( – 6, 3).
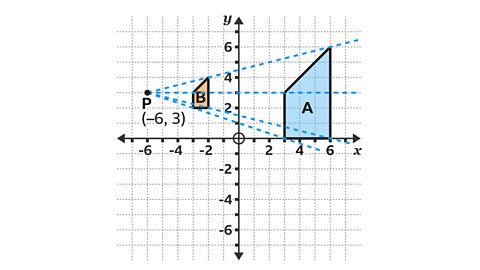
- Find the centre of enlargement by drawing lines through corresponding points on the object and image.
The lines converge at point 𝑃 with the coordinates
(– 6, 3).
Shape 𝐵 is smaller than shape 𝐴. The scale factor for a smaller shape will be between zero and one.
- Calculate the scale factor by dividing a pair of corresponding sides.
Shape 𝐵 has a vertical side with length two squares. Shape 𝐴 has a corresponding vertical side with length six squares.
Scale factor = ²⁄₆, which is simplified to ⅓.
Quiz – Enlargement
Practise what you've learned about enlargement with this quiz.
Now you've revised enlargement, why not look at area of circles and sectors?
More on Geometry and measure
Find out more by working through a topic
- count23 of 35

- count25 of 35

- count26 of 35
