Key points about calculating areas of circles and sectors

The area of a circle is the amount of two-dimensional space enclosed by its circumference.
The area of a circle is calculated using the formula:
𝐴 = 𝜋𝑟²
- The area of a sector is the two-dimensional space enclosed by two radii and an arc. Calculate the area of a sector using the formula:
𝐴 = 𝜃 ÷ 360 × 𝜋𝑟²
- Make sure you know how to find the area of a variety of shapes, as this can help when working out the area of compound shapes.
How to calculate the area of a circle
The areaA measure of the size of any plane surface. Area is measured in square units. For example, square centimetres, cm². of a circle is the amount of two-dimensional space enclosed by its circumferenceThe distance around a circle; its perimeter..
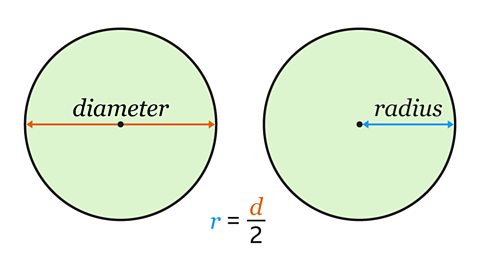
To find the area of a circle, the radiusThe distance from the centre of the circle to the circumference. Plural of radius is radii. of the circle must be known, or it must be possible to calculate it.
The FormulaA fact, rule, or principle that is expressed in terms of mathematical symbols. The plural of formula is formulae. for the area of the circle is 𝐴 = 𝜋𝑟².

Examiners expect you to use the 𝜋 button on a scientific calculator, as this will always give the most accurate answer.
However, make sure that you carefully read each question on any examination paper, as sometimes an instruction will provide an approximation to be used for 𝜋 instead.
Questions frequently ask for the final answer rounded to a stated degree of accuracy. For the non-calculator paper, questions will often state that answers should be given in terms of 𝜋.
Find out more below, along with a worked example
GCSE exam-style questions
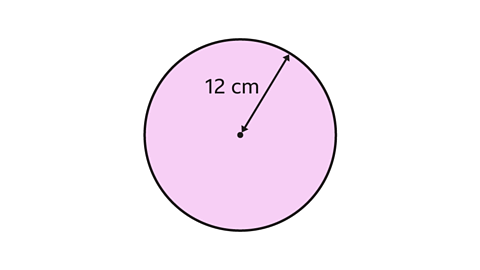
- Find the area of the circle.
Give the answer in terms of 𝜋.
The area of the circle is 144𝜋 cm².
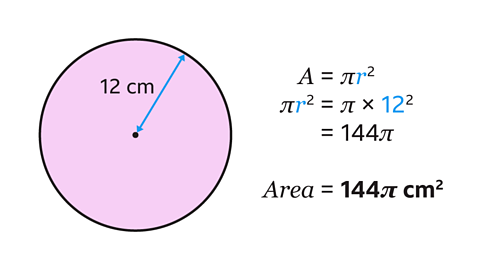
The area of a circle is found using the formula 𝐴 = 𝜋𝑟².
The radius of the circle is 12 cm.
Substitute 𝑟 = 12 into the formula for the area of the circle.
Multiply π by the square of the radius.
𝜋 × 12² = 144𝜋
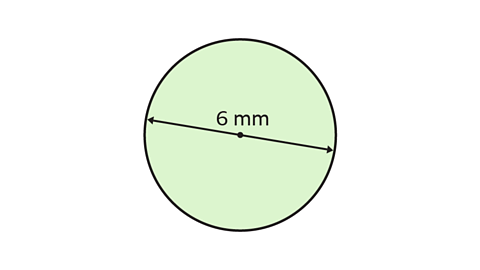
- Find the area of the circle using the approximation 𝜋 = 3·14
Give the answer to 1 decimal place.
The area of the circle is 28·3 mm².
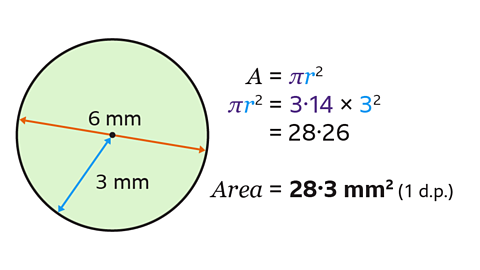
The area of a circle is found using the formula 𝐴 = 𝜋𝑟².
The diameter of the circle is 6 mm.
The radius of the circle is half of the diameter, so the radius is 3 mm.
Substitute 𝑟 = 3 into the formula for the area of the circle.
Multiply 𝜋 by the square of the radius and round to one decimal place:
3·14 × 3² = 28·26
How to calculate the area of a sector
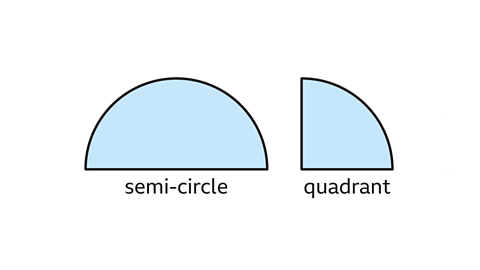
A sectorA portion of a circle with a perimeter made up of two radii and an arc. is an area enclosed by two radii and an arc.
A semi-circle is an example of a sector where the angle between the two radii is 180°. A quadrant, or quarter circle, has a 90° angle between its radii.
The area of a semi-circle is found by finding the area of a full circle and dividing by two.
The area of a quadrant is found by finding the area of a full circle and dividing by four.
For other sectors, the area is calculated using the formula.
Area of a sector = 𝜃 ÷ 360 × 𝜋𝑟²
𝜃 is the angle of the sector.

Find out more below, along with a worked example
GCSE exam-style questions

- Calculate the area of a semi-circle with diameter 10 m.
Use the approximation 𝜋 = 3·14
Give the answer to the nearest square metre.
The area of the semi-circle is 39 m².
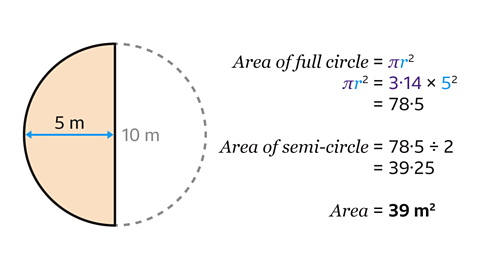
The semi-circle is half of a full circle with radius 5 m.
The formula for the area of the full circle is 𝐴 = 𝜋𝑟²
Substitute 𝑟 = 5 into the formula for the area of the circle.
Multiply 𝜋 by the square of the radius.
3·14 × 5² = 78.5.
- The area of a semi-circle is found by finding the area of a full circle and dividing by 2.
78.5 ÷ 2 = 39.25
- Find the area of the sector.
Give the answer in terms of 𝜋.
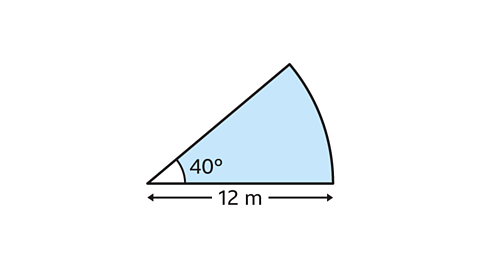
The area of the sector is 16𝜋 m².
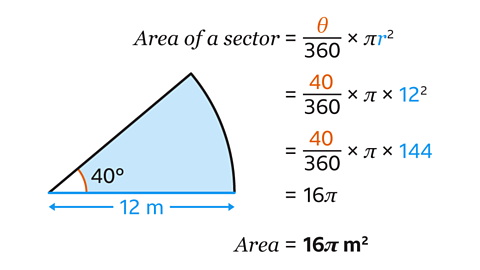
The area of a sector is calculated using the formula, area of sector = 𝜃 ÷ 360 × 𝜋𝑟².
Substitute the value of the radius and the angle into the formula.
Area of the sector = 40 ÷ 360 × 𝜋 × 12²
Working out the calculation, this simplifies to 16𝜋.
- A sector with angle 60° has an area of 24𝜋 m².
What is the length of the radius?
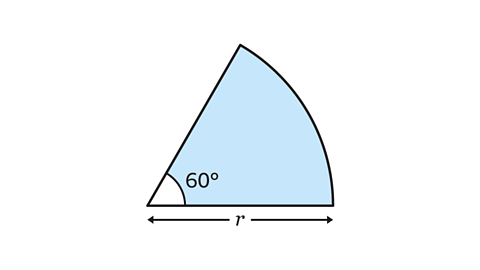
𝑟 = 12 m
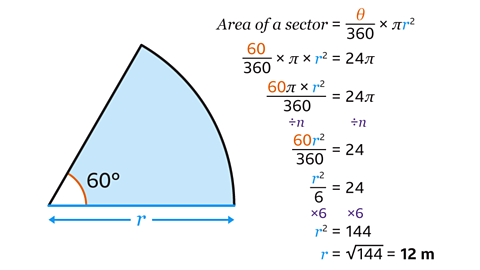
To find the value of the radius first find an expression for the area of the sector.
The area of a sector is calculated using the formula, area of sector = 𝜃 ÷ 360 × 𝜋𝑟².
- Substitute the value of 𝜃 = 60° for the angle into the formula.
60 ÷ 360 × 𝜋 × 𝑟²
This expression can be rewritten as 60𝜋 × 𝑟² ÷ 360.
An equation can be formed by equating this to the given area.
60𝜋 × 𝑟² ÷ 360 = 24𝜋
- To find the value of 𝑟, divide both sides by 𝜋.
60𝑟² ÷ 360 = 24
The fraction 60𝑟² ÷ 360 can cancel to 𝑟² ÷ 6 by dividing the numerator and denominator by 60.
Next multiply both sides of the equation by 6, which gives the equation 𝑟² = 144.
Finally, to work out the value of 𝑟, take the square root of both sides.
𝑟 = √144 = 12
How to calculate the area of compound shapes with parts of circles
A compound shapeA shape formed by combining two or more shapes. is formed by combining two or more shapes.
The areas of the combined shapes can be found separately. These areas can be added or subtracted to find the area of the compound shape.
For example, calculate the area of an annulus by finding the area of the larger circle and subtracting the area of the smaller circle.
Follow the worked example below
GCSE exam-style questions
- Calculate the area of the shaded shape.
Use the approximation 𝜋 = 3·14.
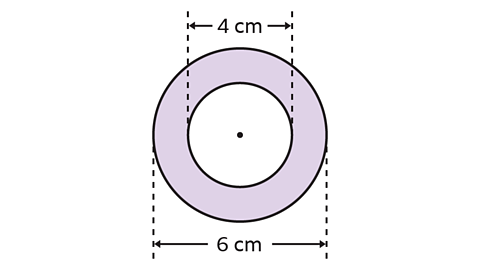
The area of the shaded shape is 15·7 cm².
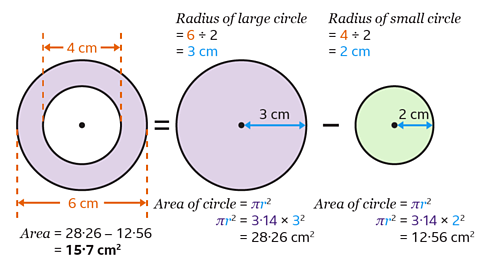
Calculate the area of the shaded shape by finding the area of the large circle and subtracting the area of the small circle.
The formula for the area of a circle is 𝐴 = 𝜋𝑟²
The diameter of the large circle is 6 cm.
Find the radius by halving the diameter, so the radius is 3 cm.
Substitute 𝑟 = 3 into the formula for the area of the circle.
3·14 × 3² = 28·26
The area of the large circle is 28·26 cm².
The diameter of the small circle is 4 cm.
Find the radius by halving the diameter, so the radius is 2 cm.
Substitute 𝑟 = 2 into the formula for the area of the circle.
3·14 × 2² = 12·56
The area of the small circle is 28·26 cm².
- Calculate the area of the shaded shape by finding the area of the large circle and subtracting the area of the small circle.
28·26 − 12·56 = 15·7
- A rectangle has two semicircles drawn inside it as shown.
Calculate the area of the shaded shape and give the answer in terms of 𝜋.
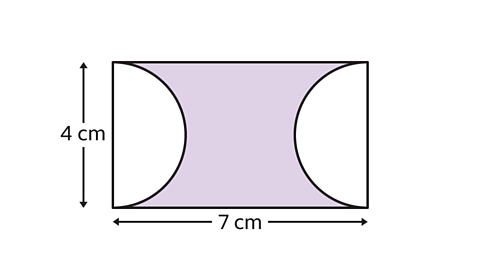
The area of the shaded shape is 28 − 4𝜋 cm².
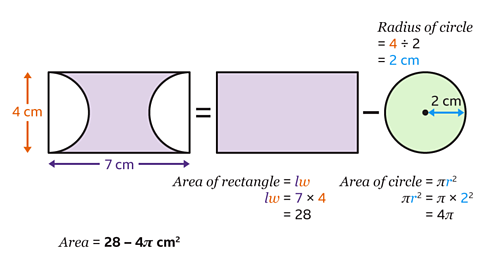
The two semi-circles make one circle.
Work out the area of the shaded shape by finding the area of the rectangle and subtracting the area of the circle.
The formula for the area of a rectangle is 𝐴 = 𝑙𝑤.
The length of the rectangle measures 7 cm and the width measures 4 cm.
7 × 4 = 28
The area of the rectangle is 28 cm².
The formula for the area of a circle is 𝐴 = 𝜋𝑟².
The diameter of the circle is 4 cm.
Find the radius by halving the diameter, so the radius is 4 cm.
Substitute 𝑟 = 2 into the formula for the area of the circle.
𝜋 × 2² = 4𝜋
The area of the small circle is 4𝜋 cm².
- Calculate the area of the shaded shape by finding the area of the rectangle and subtracting the area of the circle.
Check your understanding
Quiz – Area of circles and sectors
Practise what you've learned about area of circles and sectors with this quiz.
Now you've revised area of circles and sectors, why not look at congruent and similar shapes?
More on Geometry and measure
Find out more by working through a topic
- count19 of 35

- count20 of 35
