Key points about calculating angles using circles

Circles have different angle properties, described by a number of theorems. This is one of two guides on circle theorems, with this guide covering the following:
the angle subtended by an arc at the centre of a circle is twice the angle subtended at any point on the circumference.
the angle subtended at the circumference by a semicircle is a right angle.
the angle at the circumference of a semi-circle that is subtended by the diameter is a right angle.
opposite angles of a cyclic quadrilateral add up to 180°.
When you are confident with the theorems in this guide, have a look at the guide on How to calculate tangents and chords using the alternate segment theorem.
Make sure you are confident using other angles rules, such as angles on a straight line add up to 180° and that angles in a triangle add up to 180°, and can recognise angles in parallel lines.
Angle subtended by an arc
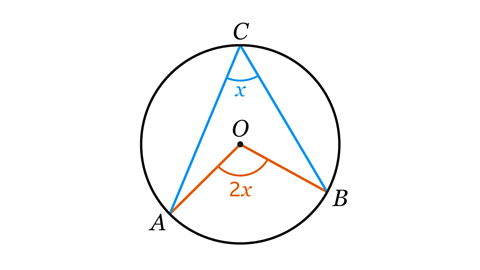
When an angle is created by lines drawn from the endpoints of an arcPart of the circumference. Named as major for over half of the circumference and minor for less than half of the circumference. to a specific point it is said to be subtendedAn angle created by lines drawn from the endpoints of a line segment or arc to a specific point. by an arc.
The angle at the centre of a circle is twice the angle at the circumferenceThe distance around a circle; its perimeter. that is subtended by the same arc.
Angle AOB in the image is twice the size of angle ACB.
Line segments AO and OB are radiusThe distance from the centre of the circle to the circumference. Plural of radius is radii. as they are the same length. A consequence of this is there can be isosceles triangleTwo sides are equal in length. Two angles are the same size. embedded within the diagram. Triangle AOB is isosceles.
Find out more, along with worked examples
GCSE exam-style questions

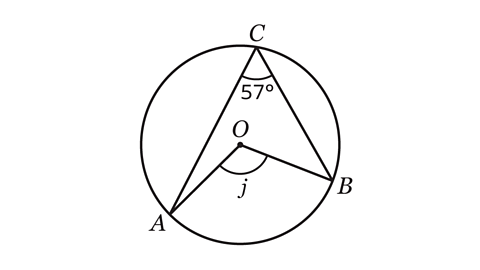
- Calculate the size of angle 𝑗.
Angle 𝑗 = 114°
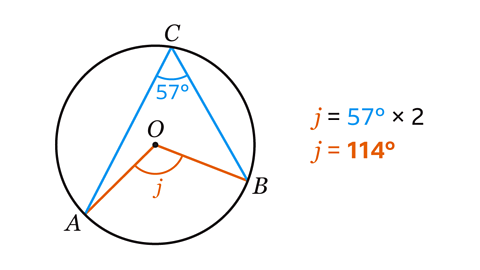
The angle at the centre of a circle is twice the angle at the circumference that is subtended by the same arc.
Angle 𝑗 is twice the size of 57°.
57 × 2 = 114
Angle 𝑗 = 114°.
- Calculate the size of angle 𝑘.
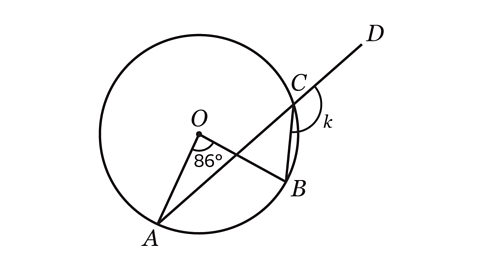
Angle 𝑘 = 137°
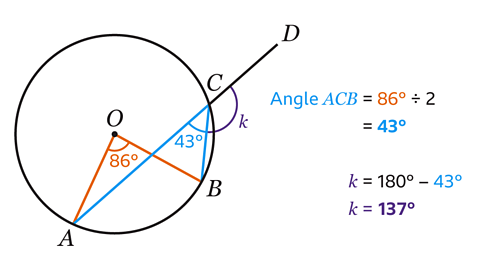
The angle at the centre of a circle is twice the angle at the circumference that is subtended by the same arc.
Angle ACB is half the size of 86°.
86 ÷ 2 = 43
Angle ACB = 43°.
Angles on a straight line add up to 180°.
Angle 𝑘 can be calculated by subtracting 43° from 180°.
180 − 43 = 137°
- Calculate the size of angle 𝑙.
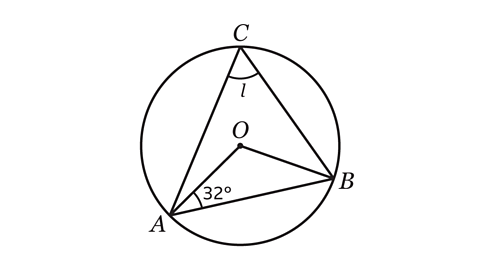
Angle 𝑙 = 58°
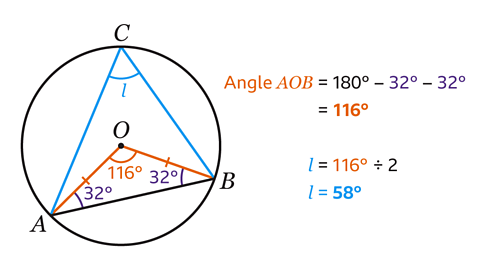
Triangle AOB is isosceles.
In an isosceles triangles two angles are equal.
Angle ABO is the same size as the angle marked as 32°.
Angles in a triangle add up to 180°. Angle AOB can be calculated by subtracting the two angles from 180°.
180 − 32 − 32 = 116
Angle AOB = 116°.
The angle at the centre of a circle is twice the angle at the circumference that is subtended by the same arc.
Angle 𝑙 is half the size of 116°.
116 ÷ 2 = 58
Angle subtended at the circumference by a semicircle
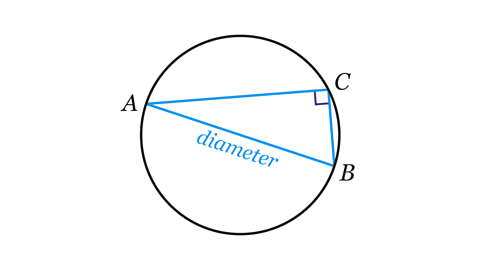
The angle at the circumferenceThe distance around a circle; its perimeter. of a semi-circleA 2D shape that is half a circle. that is subtended by the diameterThe distance across the circle, circumference to circumference, through its centre. is a right angle.
For any circle with diameter AB, if point C lies on the circumference of the circle, then angle ACB = 90°.

Follow the worked example below
GCSE exam-style questions
- By forming and solving an equation, work out the value of 𝑥.
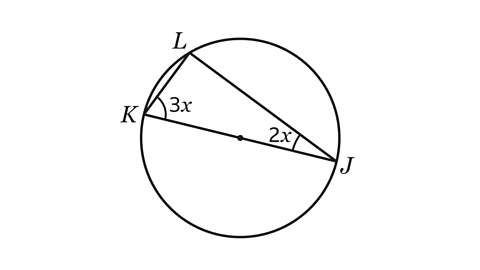
Angle 𝑥 = 18°.
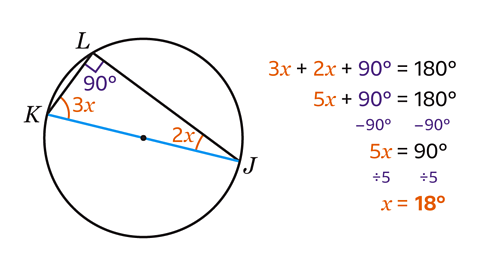
The angle at the circumference of a semi-circle that is subtended by the diameter is a right angle.
EF is the diameter of the circle.
Angle JLK = 90°.
The angles in a triangle add up to 180°.
- Form an equation by adding the angles.
3𝑥 + 2𝑥 + 90 = 180
- Find the value of 𝑥 by simplifying the equation by collecting like terms.
5𝑥 + 90 = 180
- Solve the equation by subtracting 90 from both sides.
Subtracting 90 from both sides gives 5𝑥 = 90.
- Divide both sides by 5.
𝑥 = 18°.
- Is line segment MN a diameter?
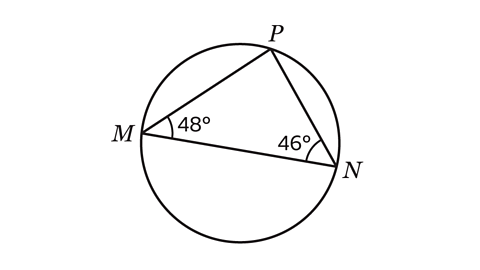
MN is not a diameter.
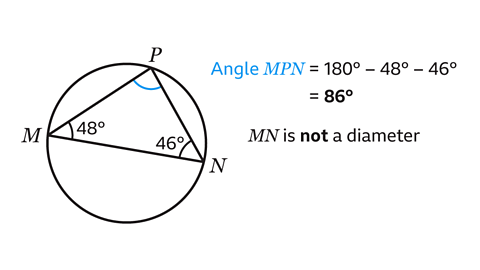
If MN is a diameter then angle MPN at the circumference is a right angle.
The angles in a triangle add up to 180°.
Angle MPN can be calculated by subtracting the two angles from 180°.
180 − 48 − 46 = 86
Angle MPN = 86°.
The angle is not a right angle, therefore MN is not a diameter.
Angles in the same segment
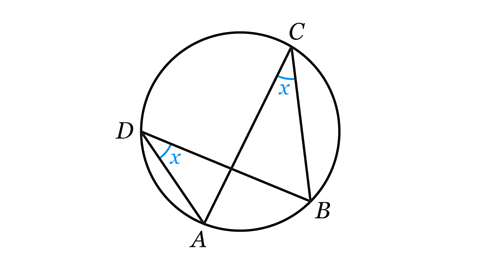
Angles subtendedAn angle created by lines drawn from the endpoints of a line segment or arc to a specific point. at the circumferenceThe distance around a circle; its perimeter. in the same segmentAn area enclosed by a chord and an arc. are equal.
The vertices C and D are on the circumference and are subtended by the same arc AB.
Angle ACB = Angle ADB

Find out more below, along with a worked example
GCSE exam-style questions

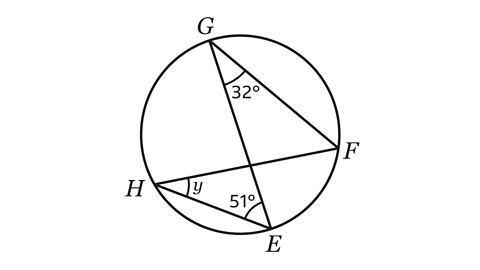
- Calculate the size of angle 𝑦.
𝑦 = 32°
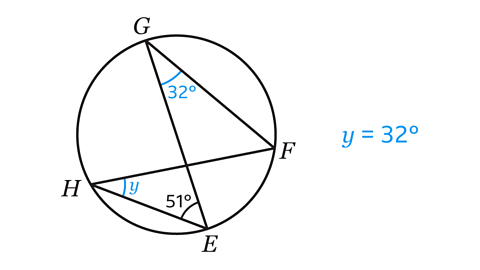
Angles subtended at the circumference in the same segment are equal.
The vertices G and H are on the circumference and are subtended by the same arc EF.
Angle EGF = Angle EHF = 32°
- Calculate the size of angle 𝑤.
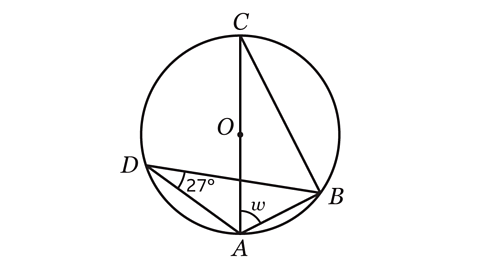
𝑤 = 63°
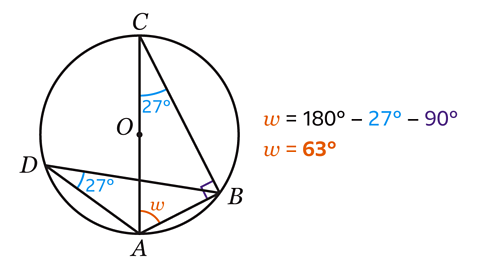
Angles subtended at the circumference in the same segment are equal.
The vertices C and D are on the circumference and are subtended by the same arc AB.
Angle ADB = Angle ACB = 27°.
The angle at the circumference of a semi-circle that is subtended by the diameter is a right angle.
AC is a diameter of the circle.
Angle ABC = 90°.
The angles in a triangle add up to 180°.
Angle 𝑤 can be calculated by subtracting the two angles from 180°.
180 − 27 − 90 = 63
- In the diagram, WZ is parallel to XY. Calculate the size of angle 𝑎.
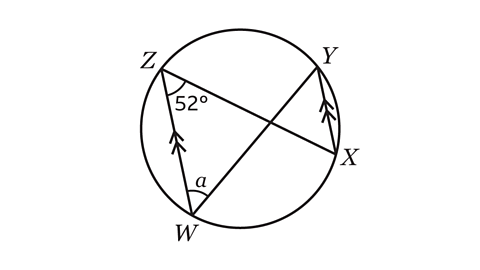
𝑎 = 52°
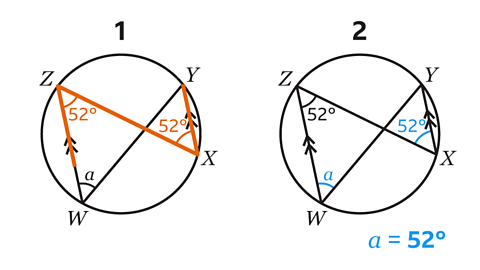
Angle YXZ is alternate to 52°. Alternate angles are equal so angle YXZ is equal to 52°.
Angles subtended at the circumference in the same segment are equal.
The vertices W and X are on the circumference and are subtended by the same arc YZ.
Angle YXZ = Angle YWZ = 52°
Angle 𝑎 = 52°.
Opposite angles in a cyclic quadrilateral
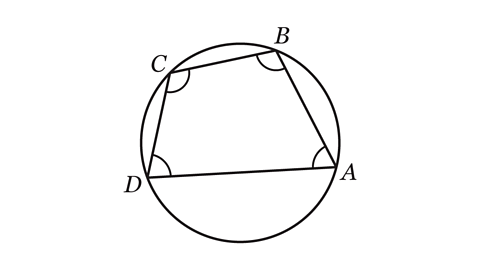
A quadrilateralA 2D shape with 4 edges and 4 vertices. where all four vertexThe point at which two or more lines cross. The corner of a shape. The plural form is vertices. lie on the circumference of a circle is called a cyclic quadrilateralA 2D shape where all 4 vertices lie on the circumference of a circle.
The opposite angles in a cyclic quadrilateral add up to 180°.
Angle A + Angle C = 180°
Angle B + Angle D = 180°

Follow the worked example below
GCSE exam-style questions

- Calculate the size of angle 𝑓.
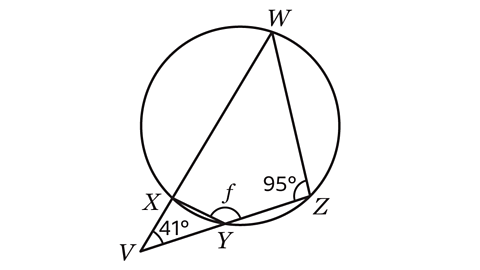
𝑓 = 136°
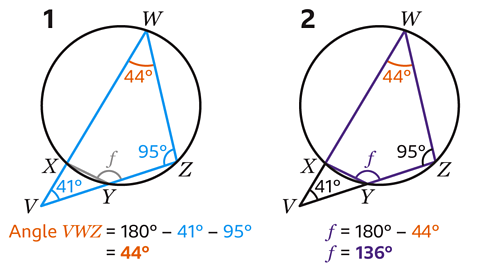
- Shape VWZ is a triangle. Angles in a triangle add up to 180°. Angle VWZ can be calculated by subtracting the two angles from 180°.
180 − 41 − 95 = 44
Angle VWZ = 44°.
- Shape WXYZ is a cyclic quadrilateral. The opposite angles in a cyclic quadrilateral add up to 180°. Angle 𝑓 is opposite the angle marked as 44°.
Angle 𝑓 is calculated by subtracting 44° from 180°.
180 − 44 = 136
- Calculate the size of angle 𝑥.
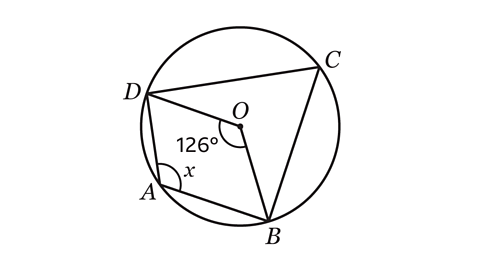
𝑥 = 117°
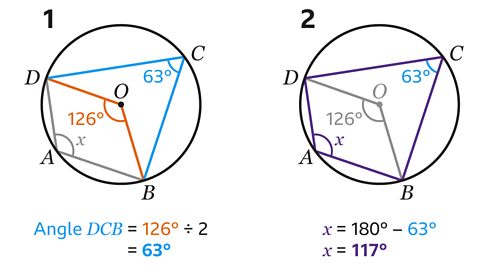
- The angle at the centre of a circle is twice the angle at the circumference that is subtended by the same arc. Angle DCB is half of angle DOB.
126 ÷ 2 = 63
Angle DCB = 63°.
- Shape ABCD is a cyclic quadrilateral. The opposite angles in a cyclic quadrilateral add up to 180°.
Angle 𝑥 is opposite the angle marked as 63°.
Angle 𝑥 is calculated by subtracting 63° from 180°.
180 − 63 = 117
Angle 𝑥 = 117°.
- The diagram shows a cyclic quadrilateral.
𝑥 : 𝑦 = 2 : 1
Calculate the size of angle 𝑧.
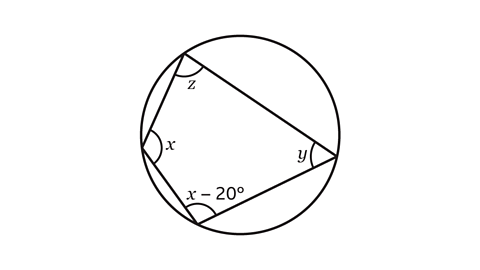
𝑧 = 80°
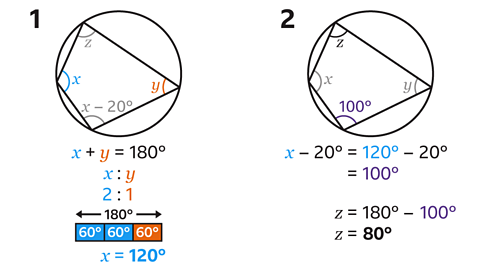
- The shape is a cyclic quadrilateral. The opposite angles in a cyclic quadrilateral add up to 180°.
𝑥 + 𝑦 = 180
The angles 𝑥 and 𝑦 are in the ratio 2 : 1.
The ratio is 3 parts in total.
- Divide 180° by 3 to find the value of each part.
180 ÷ 3 = 60
Each part is worth 60°.
Angle 𝑥 is two parts, so angle 𝑥 = 120°.
- Given angle 𝑥 = 120°, the angle marked 𝑥 − 20° can be calculated.
120 − 20 = 100
The angle opposite 𝑧 is equal to 100°.
The opposite angles in a cyclic quadrilateral add up to 180°.
Angle 𝑧 is opposite the angle marked as 100°.
- Calculate angle 𝑧 by subtracting 100° from 180°.
180 − 100 = 80
Check your understanding
Quiz – Calculating angles with circles
Practise what you've learned about calculating angles with circles with this quiz.
Now you've revised calculating angles with circles, why not look at circumference and arc length?
More on Geometry and measure
Find out more by working through a topic
- count19 of 35

- count20 of 35

- count21 of 35
