Key points about angles in parallel lines

parallel lines Lines which never meet and stay the same distance apart. Parallel lines are indicated by a pair of arrows. are two or more straight lines that remain the same distance apart and never intersect.
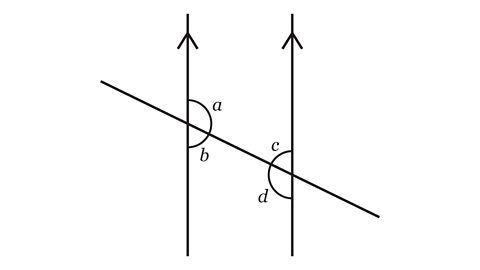
A transversal A line which crosses a set of parallel lines. is a line which crosses two or more parallel lines. The point where it crosses is called a point of intersectionThe location where two or more lines meet.
When a transversal intersects a pair of parallel lines, various types of angles are formed within the parallel lines: alternate anglesAngles on opposite sides of the transversal within the parallel lines. , corresponding angles Angles at the same position within each intersection. and co-interior anglesAngles on the same side of the transversal, between the two parallel lines. .
Make sure you are confident with solving linear equations before working with angles written as algebraic expressions.
Check your understanding
What are alternate angles?
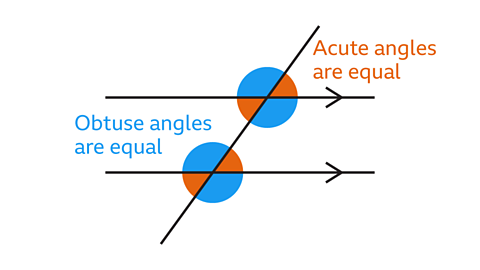
When a transversal intersects a pair of parallel lines, the angles at both points of intersection are related.
Along a specific transversal, all of the are the same size.
All of the are the same size.
Pairs of angles can be given special names.
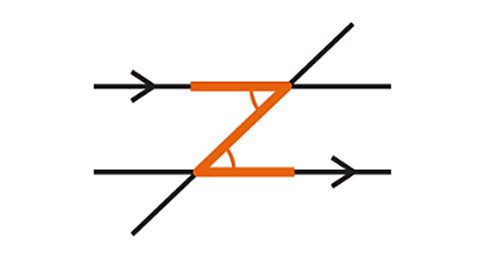
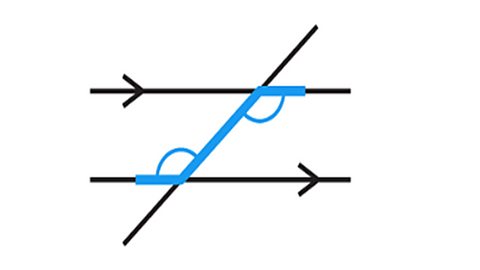
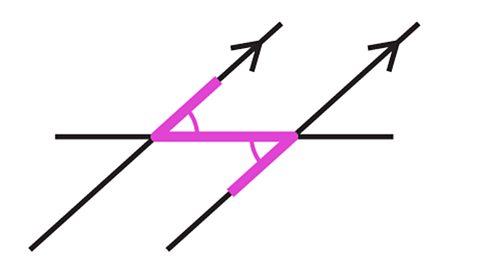
Alternate angles are on opposite sides of the transversal within the parallel lines.
- Alternate angles are always equal in size.
- When looking for alternate angles, it can useful to look for a Z-shape.
- The Z-shape can be backwards, sideways or upside down.

Follow the worked example below
GCSE exam-style questions

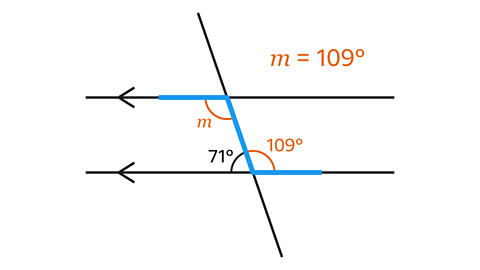
- Work out the size of angle 𝑚.
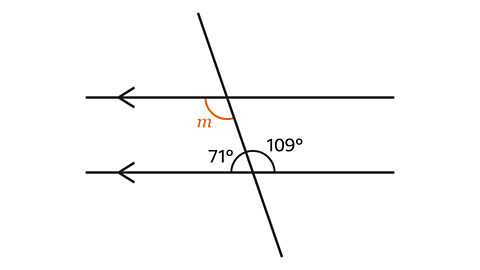
Angle 𝑚 = 109°.
The angle 𝑚 makes an alternate pair with the angle 109°.
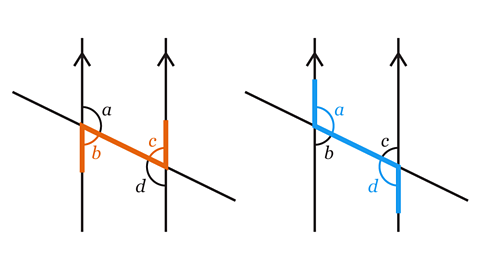
- Which pairs of angles are alternate?
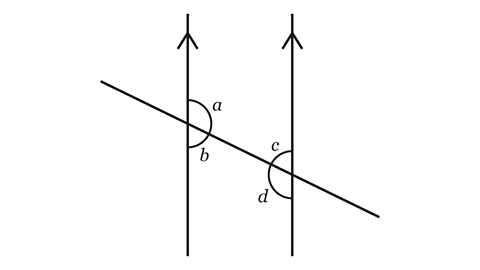
Angles 𝑏 and 𝑐 form one pair of alternate angles.
Angles 𝑎 and 𝑑 form another pair of alternate angles.
- Set up and solve an equation to find 𝑥.
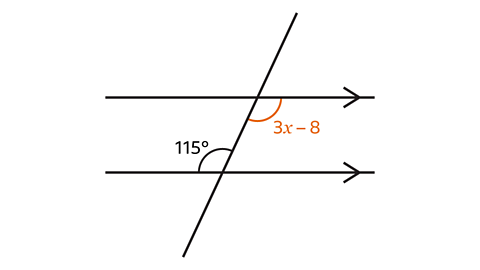
Angle 𝑥 is 41°.
Angles 3𝑥 – 8 and 115° are alternate.
Alternate angles are equal, so 3𝑥 – 8 = 115.
To find the value of 𝑥, first add 8 to both sides. This produces the equation 3𝑥 = 123
Now divide both sides by 3.
3𝑥 ÷ 3 = 𝑥 and 123 ÷ 3 = 41.
The value of 𝑥 = 41°.
What are corresponding angles?
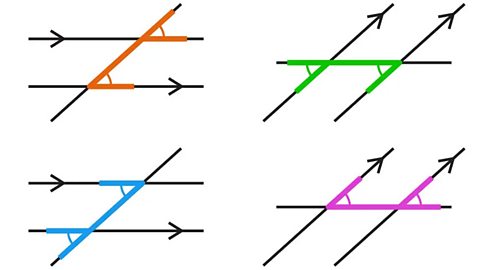
Corresponding angles occur at the same position within each intersection.
Corresponding angles are always equal in size.
When looking for corresponding angles, it can be helpful to look for an F- shape.
The F-shape can be backwards, sideways or upside down.

Follow the worked example below
GCSE exam-style questions

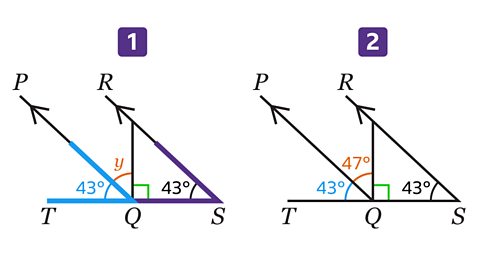
- 𝑃𝑄 is parallel to 𝑅𝑆.
Work out the size of angle 𝑦.
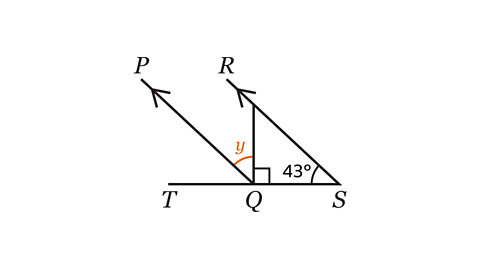
Angle 𝑦 is 47°.
1: The angle adjacent to angle 𝑦 is corresponding to 43°. Corresponding angles are equal so this angle is equal to 43°.
2: Angle 𝑦, 43° and the right-angle are adjacent angles on a straight line. Adjacent angles on a straight line add up to 180°.
𝑦 = 180 – 90 – 43 = 47
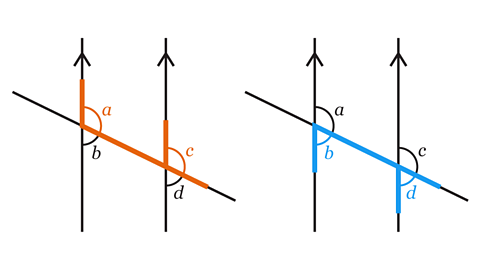
- Which pairs of angles are corresponding?
Angles 𝑎 and 𝑐 form one pair of corresponding angles.
Angles 𝑏 and 𝑑 form another pair of corresponding angles.
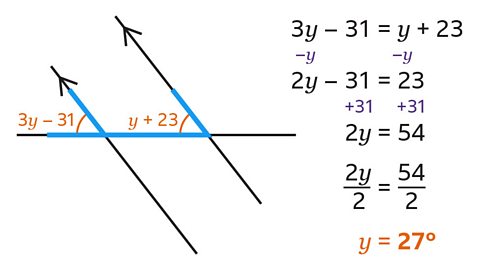
- Set up and solve an equation to find 𝑦.
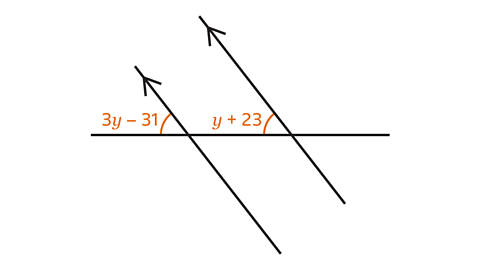
Angle 𝑦 is 27°.
Angles 3𝑦 – 31 and 𝑦 + 23 are corresponding.
Corresponding angles are equal so
3𝑦 – 31 = 𝑦 + 23
- To find the value of 𝑦, first subtract 𝑦 from both sides which gives the equation
2𝑦 – 31 = 23
- Now add 31 to both sides which gives
2𝑦 = 54
- Finally, divide both sides by 2.
2𝑦 ÷ 2 = 𝑦
54 ÷ 2 = 27
What are co-interior angles?
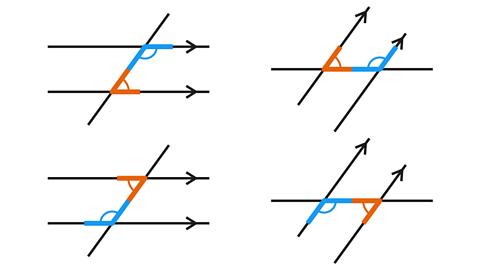
Co-interior angles (or allied angles) occur on the same side of the transversal, between the two parallel lines.
- Co-interior angles add up to 180°.
- When looking for corresponding angles, it can be helpful to look for a C-shape.
- The C-shape can be backwards, sideways or upside down.

Follow the worked example below
GCSE exam-style questions

- Trapezium 𝐴𝐵𝐶𝐸 is made from parallelogram 𝐴𝐵𝐶𝐷 and isosceles triangle 𝐴𝐷𝐸.
𝐴𝐸 = 𝐷𝐸
Work out the size of angle 𝐴𝐸𝐷.
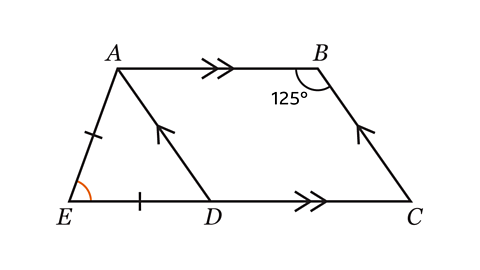
Angle 𝐴𝐸𝐷 = 70°
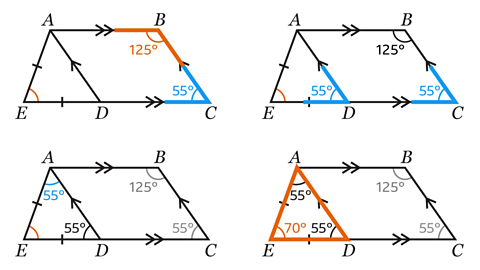
- Angle 𝐴𝐵𝐶 and 𝐵𝐶𝐷 are co-interior angles.
Co-interior angles add up to 180°, so angle 𝐵𝐶𝐷 = 180 – 125 = 55°.
Angle 𝐵𝐶𝐷 and 𝐴𝐷𝐸 are corresponding angles. Corresponding angles are equal so angle 𝐴𝐷𝐸 = 55°.
Since triangle 𝐴𝐷𝐸 is isosceles, angles 𝐴𝐷𝐸 and 𝐷𝐴𝐸 are equal. Angle 𝐷𝐴𝐸 = 55°.
The angles in a triangle add up to 180°. Angle 𝐴𝐸𝐷 = 180 – 55 – 55 = 70.
Angle 𝐴𝐸𝐷 = 70°.
- Which pairs of angles are co-interior?
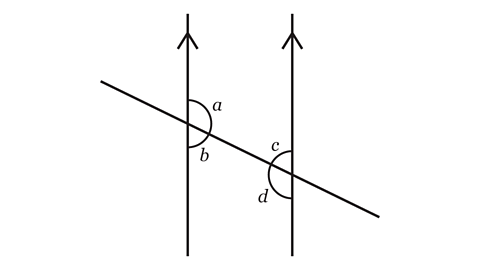
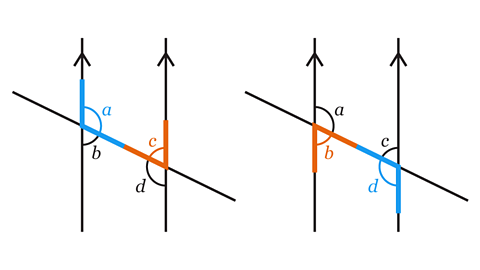
Angles 𝑎 and 𝑐 form one pair of co-interior angles.
Angles 𝑏 and 𝑑 form another pair of co-interior angles.
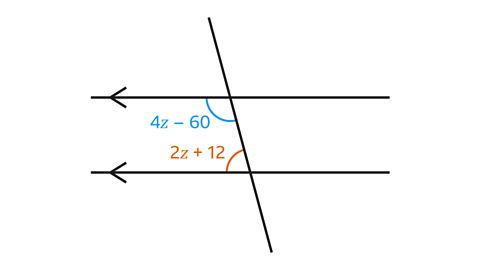
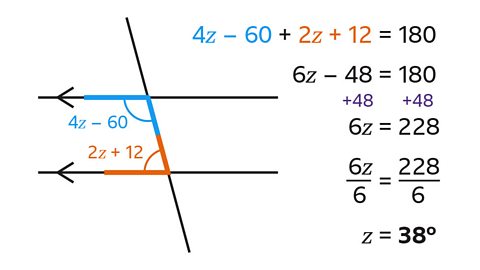
- Set up and solve an equation to evaluate 𝑧.
𝑧 = 38°
Angles 4𝑧 – 60 and 2𝑧 + 12 are co-interior.
Co-interior angles add up to 180°, so the equation is
4𝑧 – 60 + 2𝑧 + 12 = 180
- Collect like terms, which simplifies to the equation
6𝑧 – 48 = 180
- Now add 48 to both sides. Adding 48 to both sides produces the equation
6𝑧 = 228
- Finally divide both sides by 6.
6𝑧 ÷ 6 = 𝑧 and 228 ÷ 6 = 38.
The value of 𝑧 is 38°.
Quiz - Angles in parallel lines
Practise what you've learned about angles in parallel lines with this quiz.
Now you've revised angles in parallel lines, why not look at bearings?
More on Geometry and measure
Find out more by working through a topic
- count3 of 35

- count4 of 35

- count5 of 35

- count6 of 35
