Key points about ruler and compass constructions

In maths, a construction is an accurate drawing.
Besides constructing triangles, there are two main constructions which can be done using a ruler, a pair of compasses and a pencil:
- A line bisector, which is a line that cuts another line into two equal parts and meets it at a right angle. As the lines meet at 90° it is also called a perpendicularPerpendicular lines are at right angles to each other. bisector.
- An angle bisector, which is a line that cuts an angle into two equal size angles.
After the construction is finished, it is important to leave any construction lines in place. This is important in exams to maximise the marks awarded.
To be certain your constructions are precise, make sure you are confident at measuring accurately with a ruler and at drawing arcs with a pair of compasses.
How to construct a perpendicular of a line
A bisector is a line which cuts another line exactly in half.
A perpendicular bisector cuts a line exactly in half and intersects it at a right angle. It can be constructed using a ruler and pair of compasses.
Watch the example below
Read the steps below to see the full method outlined.
To construct a perpendicular bisector:
Using a ruler, draw a straight line. This line is sometimes given in the question.
Place the compasses on the left-hand endpoint of the line and set them to just over halfway along the line. Draw an arcThe curve between two points on the circumference of a circle. which spans above and below the line.
Without changing the distance of the compasses, repeat this with the right-hand endpoint of the line.
The arcs should intersect in two places. Draw a line between each point of intersection of the arcs. The point of intersection of the perpendicular bisector and the original line is exactly halfway along the line.
GCSE exam-style questions
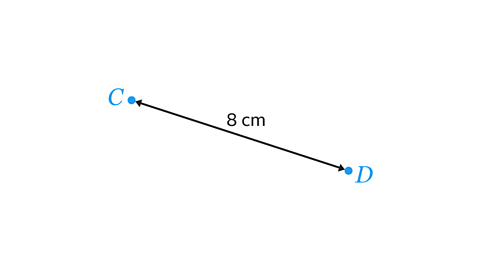
- Points 𝐶 and 𝐷 are 8 cm apart.
Use a ruler and pair of compasses to construct the perpendicular bisector of 𝐶𝐷. Make sure to show all your construction arcs.
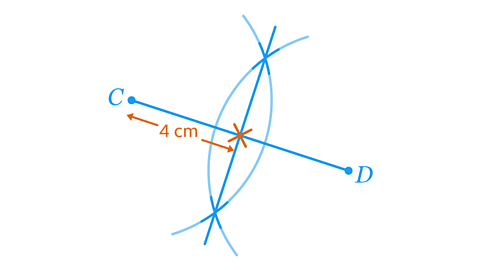
The perpendicular bisector should cut line 𝐶𝐷 in half. Constructed accurately, the distance between 𝐶 and the midpoint measures 4 cm.
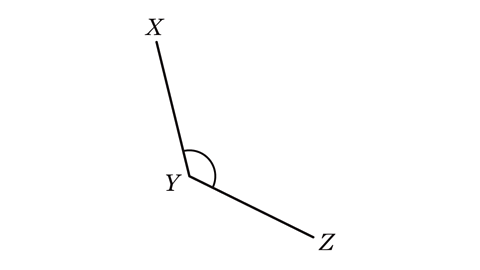
- Jack has constructed a line bisector of line XY. What mistake have they made?
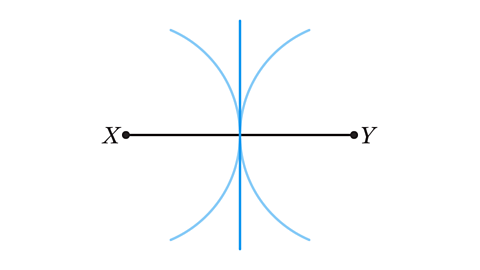
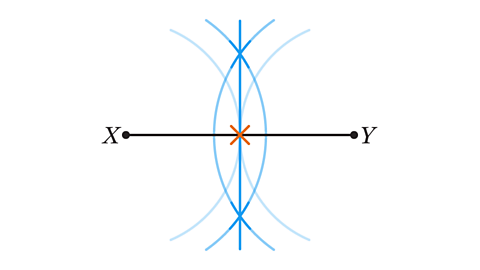
Jack did not open the pair of compasses to just over halfway along the line. This meant their arcs did not intersect above and below the lines.
How to draw a perpendicular from a point on a line
Watch the example below
Read the steps below to see the full method outlined.
To construct a perpendicular from a point on a line:
Place the compasses on the point and draw an arc which crosses the line once on either side of the point.
Place the compasses on the left-hand point of intersectionThe location where two or more lines meet, set them to just over halfway along the line, and draw another arc which intersects the first arc.
Without changing the compasses, do the same on the right-hand side.
Draw a line between the point of intersection of the two new arcs and the point.
Remember: even the smallest inaccuracy at any point will create an error in the final angle. A sharp pencil is important to ensure accuracy.
How to draw a perpendicular bisector from a point to a line
Watch the example below
Read the steps below to see the full method outlined.
To construct a perpendicular from a point to a line:
Place the compasses on the point and set them to just below the line. Draw an arc which crosses the line twice.
Place the compasses on the left-hand point of intersection between the arc and the line, then draw another arc below the line.
Without changing the compasses, do the same on the right-hand side.
Draw a line between the point of intersection of the new arcs and the point.
How to bisect an angle
An angle bisectorA line which cuts an angle in half. cuts an angle into two angles of equal size. It can be constructed using a ruler and a pair of compasses.
Watch the example below
Read the steps below to see the full method outlined.
To construct an angle bisector:
Using a ruler, draw two lines which meet at a point. This makes an angle. This angle is sometimes given in the question.
Place the compasses at the point where the two lines meet and draw an arc which crosses both arms of the angle.
At each point of intersection of the arms and the arc, draw smaller arcs.
Draw a line between the point of point of intersectionThe location where two or more lines meet of the new arcs and the point where both lines meet.
This method, combined with other constructions, can be used to construct angles accurately which measure 30° or 45°.
GCSE exam-style questions
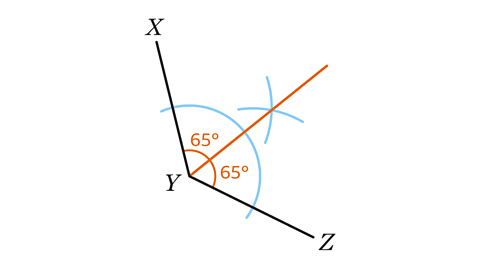
- Angle 𝑋𝑌𝑍 measures 130°. Use a ruler and pair of compasses to construct the angle bisector of 𝑋𝑌𝑍. Show all your construction arcs.
The angle bisector should cut angle 𝑋𝑌𝑍 in half. Constructed accurately, each angle measures 65°.
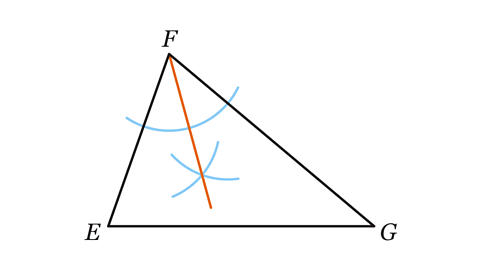
- Anika was asked to construct an angle bisector of angle 𝐸𝐹𝐺 in triangle 𝐸𝐹𝐺. What mistake has she made?
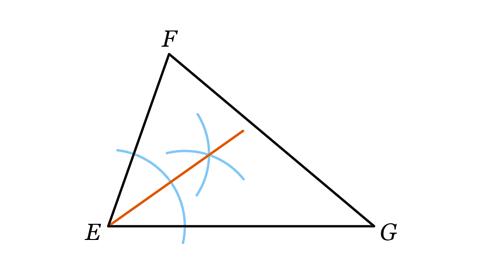
Anika has bisected the wrong angle. She has bisected angle 𝐸 instead of 𝐹.
Check your understanding
How much do you know about ruler and compass constructions?
Quiz – Ruler and compass constructions
Practise what you've learned about ruler and compass constructions with this quiz.
Now you've revised ruler and compass constructions, why not check out circumference and arc length?
More on Geometry and measure
Find out more by working through a topic
- count7 of 35

- count8 of 35

- count9 of 35

- count10 of 35
