Key points about loci

A locus is a path formed by a set of points that satisfy a rule. The plural is loci.
A locus can be a straight line, a curve or a combination of the two.
The shape of the locus of points depends on the given rule.
Make sure you are confident at drawing arcs with a pair of compasses and constructing bisectors, in order to make your loci precise.
How to construct loci
A locus is a set of points, forming a line or curve, which satisfy a set of conditions.
Loci are constructed using a pencil, ruler and a pair of compasses.
The locus of points equidistantEqual distance between two objects. from a point is a circleA shape consisting of points that are the same distance from the centre of the shape. .
The locus of points equidistant from a line is a straight line.
Sometimes a region can be bound or enclosed by a locus.
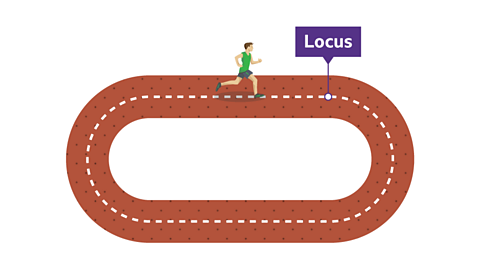
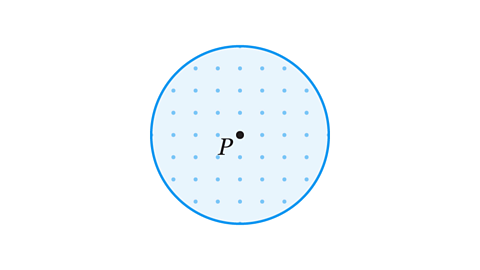
Find out more about constructing loci below, with worked examples
Locus that is a fixed distance from a point
Locus that is equidistant from a line
GCSE exam-style questions

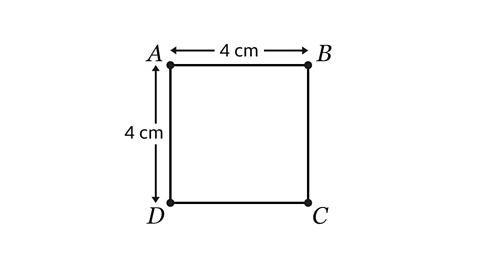
- Shape 𝐴𝐵𝐶𝐷 is a square. Shade the region within the square that is less than 3 cm from 𝐵.
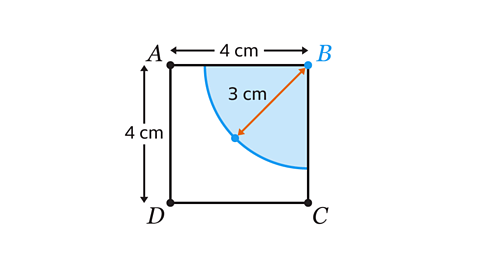
The shaded region is a called a quadrant.
Set the compasses to 3 cm apart. Put the compass point on vertex 𝐵 and construct an arc of radius 3 cm. Shade the region enclosed by the arc and the lines 𝐴𝐵 and 𝐵𝐶.
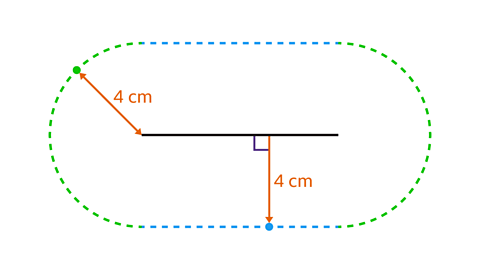
- Draw accurately the locus of points which are 4 cm around the line.
The locus takes the form of a racing track.
Construct the locus above and below the line using a pencil and ruler. These horizontal lines need to be a perpendicular distance of 4 cm from the original line.
Construct the locus at each end of the line using a pair of compasses. Set the compasses to 4 cm apart. Put the compass point on the right-hand end of the line and construct an arc of radius 4 cm.
Repeat the process putting the compass point on the left-hand end of the line.
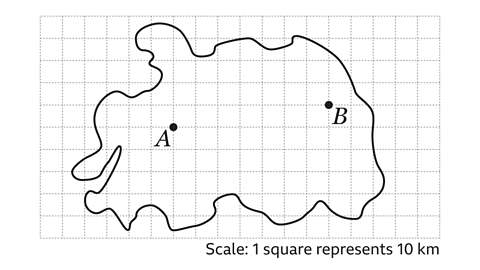
- Two mobile phone masts are on an island at A and B.
The scale of the diagram is 1 square represents 10 km.
Both masts have a range of 40 km.
Shade on the map to show the areas of the island where mobile phones do not get a signal.
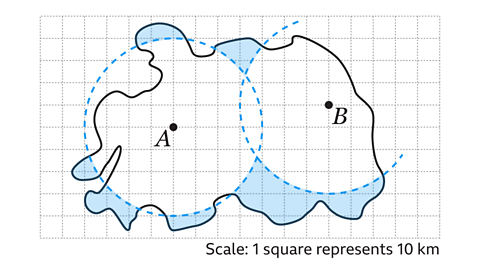
The mobile phone signal is equivalent to a locus of points equidistant from a point.
The locus of each mast is a circle of radius four squares centred at the mast.
The shaded region beyond the two circles indicates where you cannot get a phone signal.
Loci with bisectors
Some loci can require more complex construction techniques.
- The locus of points equidistant from two points is a line bisectorA perpendicular line which cuts a line in half. .
- The locus of points equidistant from two lines is an angle bisectorA line which cuts an angle in half. .
Find out more below, with worked examples
Locus equidistant from two points
Locus equidistant from two lines
GCSE exam-style questions
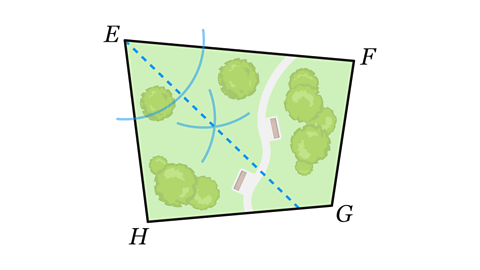
- 𝐸𝐹𝐺𝐻 represents the shape of a park.
A straight path across the park starts at 𝐸 and is the same distance from 𝐸𝐹 and 𝐸𝐻.
Use a ruler and compasses to construct the position of the path.
The locus of points equidistant from two lines is an angle bisector.
Construct an angle bisector at angle 𝐸.
- The diagram represents a triangular garden 𝑋𝑌𝑍.
The scale of the diagram is 1 cm represents 1 m.
A tree is to be planted in the garden so that it is nearer to 𝑌 than 𝑍, and within 6 m of point 𝑋.
On the diagram, shade the region where the tree may be planted.
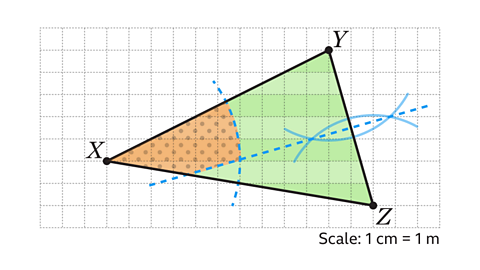
To plant the tree so that it is nearer to 𝑌 than 𝑍 requires a line bisector of 𝑌𝑍.
All the points above the bisector are closer to 𝑌 than 𝑍.
For the tree to be within 6 m of point 𝑋, the points must be within a circular locus of radius six squares centred at 𝑋.
The shaded region shows the area that satisfies both criteria.
Check your understanding
Quiz – Loci
Practise what you've learned about loci with this quiz.
Now you've revised loci, why not look at circumference and arc length?
More on Geometry and measure
Find out more by working through a topic
- count8 of 35

- count9 of 35

- count10 of 35

- count11 of 35
