Key points about line and rotational symmetry

Two dimensional polygonA closed 2D shape bounded by straight lines. can have symmetrical properties.
There are two types of symmetry:
Reflective symmetry is when a shape can be folded in half, with either side of the fold being a mirror image of the other.
Rotational symmetry is when a shape can be rotated and it still looks the same. The number of times it looks the same is called the .
Make sure you are confident with the names of quadrilaterals and polygons before working with symmetry.
Video – Rotational symmetry
Watch this video to learn how to find the order of rotational symmetry for different shapes, including square, parallelogram, kite and rhombus.
Rotational symmetry
All squares have a rotational symmetry of order 4.
This means that in one full rotation of 360 degrees about its centre, there are 4 positions where the shape looks identical to its starting position.
When finding the order of rotational symmetry, it's helpful to mark a reference point to know when you've rotated through the full 360 degrees.
For example, you could choose the top right vertex, or corner, of this rectangle as your reference point.
Be careful not to confuse the reference point with the centre of rotation, which will be in the middle of the shape.
Then, by rotating about the centre until the reference point is back in the top right position, you can see that the rectangle matches its starting position twice.
So, rectangles have a rotational symmetry of order 2.
Now, let's see how to determine the order of rotational symmetry of a parallelogram.
This time, using tracing paper.
For the first step, trace the given shape on tracing paper.
Then, choose your reference point, for example, the top right vertex, and draw a dot to represent it on both the given shape and your trace.
When these two dots match up, you know you have rotated the full 360 degrees.
Next, place the point of your pencil at the centre of rotation and then rotate the tracing paper around this.
Making sure to count the number of times the edges and vertices of the two shapes match up.
For the parallelogram, that's 2, so parallelograms have rotational symmetry of order 2.
Finally, let's find the order of rotational symmetry of these three shapes: a trapezium, a kite and a rhombus.
Remember, you need to draw each shape on tracing paper, choose a reference point, and then rotate the paper about the centre.
The trapezium matches the starting position only once in 360 degrees, so the order of rotational symmetry is 1.
The kite also only matches once, so the order is also 1.
And the rhombus matches twice, so the order is 2.
What is reflective symmetry?
If a 2D shape can be folded in half, with either side of the fold being a mirror image of the other, then it has a line of symmetry.
A line of symmetry is an imaginary line, through the centre point, which splits a shape equally in two. Lines of symmetry are indicated by a dotted line.
A mirror can also be used to help find lines of symmetry. When a mirror is placed in a position on a shape, either vertically, horizontally or diagonally and the reflection matches the other half, this indicates a line of symmetry.
Find out more below
GCSE exam-style questions

- How many lines of symmetry does a kite have?

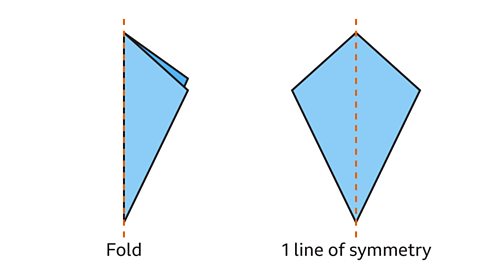
A kite can be folded vertically down the middle. Both sides of the fold are the mirror image of each other.
The kite has 1 line of symmetry.
- Which shape has two lines of symmetry?
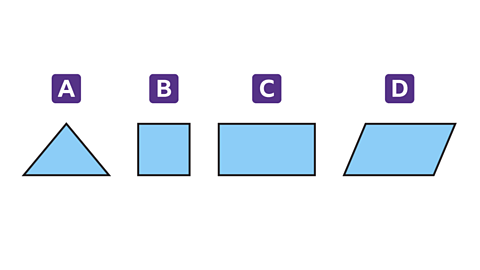
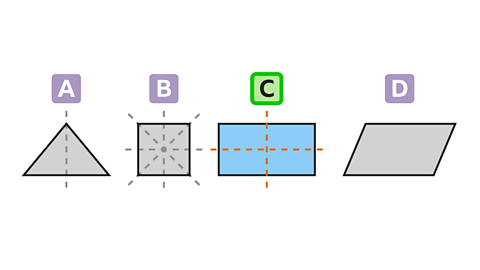
Shape C has 2 lines of symmetry.
Shape A has 1 line of symmetry.
Shape B has 4 lines of symmetry.
Shape D has no lines of symmetry.
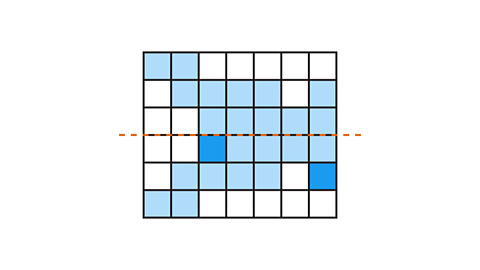
- What is the least number of squares that can be shaded for the shape to have 1 line of symmetry?
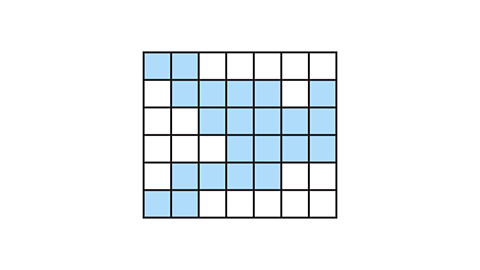
Two squares.
Shading the two squares shown gives the shape a horizontal line of symmetry.
What is rotational symmetry?

A shape has rotational symmetry if it looks the same in more than one position, when the shape is rotated about its centre.
The number of times it looks the same through a full turn (360°) is called the order of rotational symmetry.
For example, a shape that looks the same six times through a full turn has a rotational symmetry of order 6.
A shape with rotational symmetry of order 1 can also be described as having no rotational symmetry.

Find out more below, along with a worked example
GCSE exam-style questions

- Which shape has rotational symmetry of order 4?
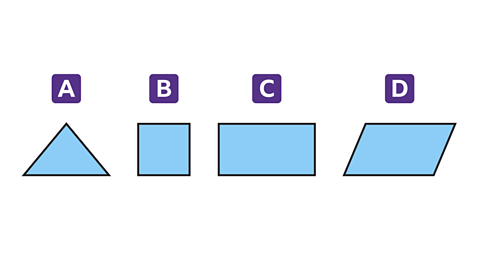
Shape B has rotational symmetry of order 4.
Shape A has no rotational symmetry.
Shape C and D have rotational symmetry of order 2.
- What is the least number of squares that can be shaded for the shape to have rotational symmetry of order 2?
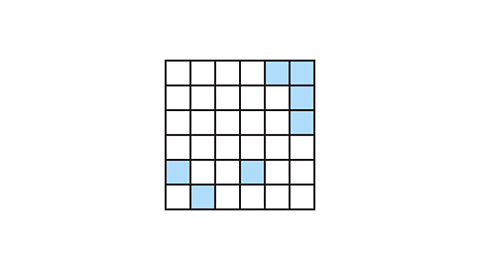
Three squares.
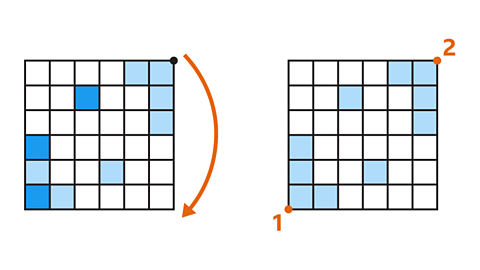
Shading the three squares shown gives the shape rotational symmetry of order 2.
- What is the order of rotational symmetry for a regular hexagon?
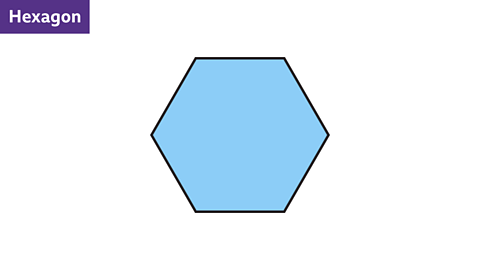
A regular hexagon has rotational symmetry of order six.
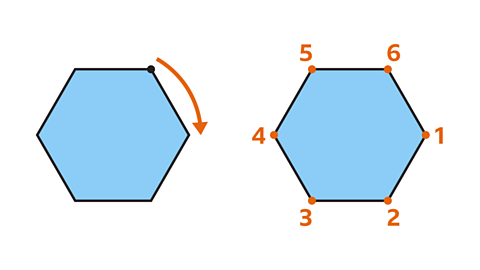
Through a full turn (360°) there are 6 positions where the reference point would make the shape look the same as the original.
Symmetry of quadrilaterals and polygons
Quadrilaterals show various symmetrical properties depending on their type.
For regular polygonA closed 2D shape bounded by straight lines. All sides are equal in length. All angles are equal. :
- The number of lines of symmetry is equal to the number of sides.
- The order of rotational symmetry is equal to the number of sides.
Find out more below
GCSE exam-style questions
- A quadrilateral has no lines of symmetry.
It has rotational symmetry of order 2.
What type of quadrilateral is the shape?
The answer is parallelogram.
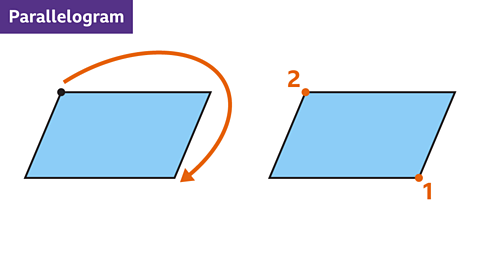
A parallelogram has no lines of symmetry.
It has rotational symmetry of order 2.
- Which regular polygon has 8 lines of symmetry and rotational symmetry of order 8?
The answer is octagon.
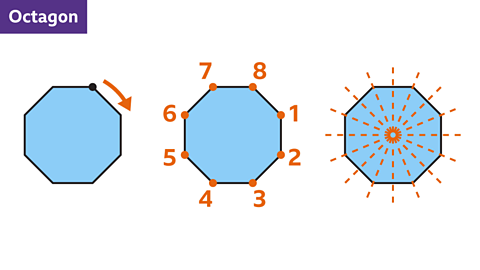
For regular polygons, both the number of lines of symmetry and order of rotational symmetry is equal to the number of sides.
The regular polygon with 8 sides is called an octagon.
Check your understanding
Quiz – Line and rotational symmetry
Practise what you've learned about line and rotational symmetry with this quiz.
Now you've revised line and rotational symmetry, why not learn about nets, plans and elevations?
More on Geometry and measure
Find out more by working through a topic
- count5 of 35

- count6 of 35

- count7 of 35

- count8 of 35
