Properties of quadrilaterals - KS3 Maths

Key points

Properties of a square. A series of four images. The first image is a composite image showing all the properties of a square. The second image is a square. Each side of the square is marked with a hash. Written below: four equal sides. The third image is a square. The two horizontal sides have been coloured orange and marked with an arrow to indicate they are parallel. The two vertical sides have been coloured blue and marked with two arrows to indicate they are parallel. Written below: two pairs of parallel sides. The fourth, and final image is a square. Each corner has been marked with a pink right angle symbol. Written below: four right angles. — Image caption,
A square has four sides that are equal in length.

All are with four . They are classified by the comparative lengths and position of their edges.

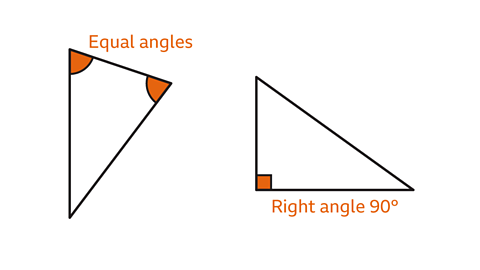
The angles in a quadrilateral always sum to 360°.
The properties of a quadrilateral include additional facts relating to their and their .
A specific property may apply to more than one quadrilateral.

Properties of squares, rhombuses, and rectangles

To classify a as a a or a , check for the following properties.

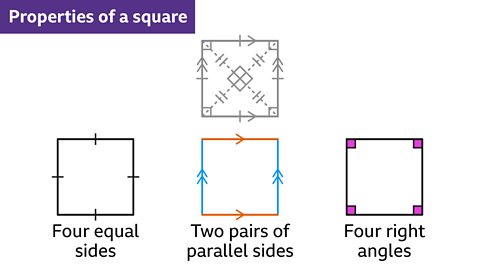
A square has:
- Four sides equal in length.
- Two pairs of parallel sides.
- Four right angles.
- that are equal in length.
- Diagonals that each other and are .
- Four .
- of
A rhombus has:
- Four sides equal in length.
- Two pairs of parallel sides.
- Two pairs of equal opposite angles.
- Diagonals that bisect each other and are perpendicular.
- Two lines of symmetry.
- Rotational symmetry of order 2
A rectangle has:
- Two pairs of opposite sides that are equal in length.
- Two pairs of parallel sides.
- Four right angles.
- Diagonals that are equal in length.
- Diagonals that bisect each other.
- Two lines of symmetry.
- Rotational symmetry of order 2

Examples

Skip image gallery

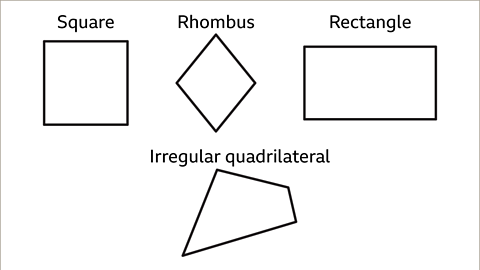
Image caption,
All quadrilaterals have four sides and four angles. The lengths and position of the edges help to identify the quadrilateral. A quadrilateral that is not a specific type is called an irregular quadrilateral.
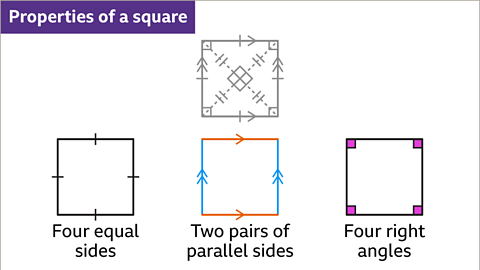
Image caption,
A square has four sides that are equal in length. Equal lengths are shown on the diagram by hash marks annotated on each side. The opposite sides are parallel, meaning the square has two pairs of parallel sides. The parallel sides are annotated with matching arrowhead(s) in the same direction. The angles are all right angles. The right angles are marked on the diagram as a small square at each vertex.
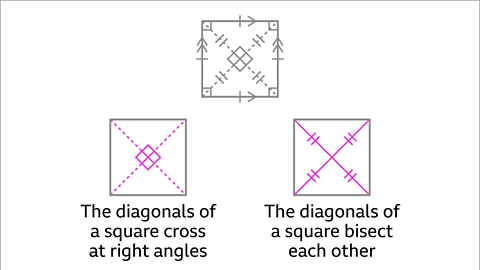
Image caption,
The diagonals of a square are equal in length. The diagonals are perpendicular, they cross at right angles. The diagonals of a square bisect each other, that means they cut each other in half.
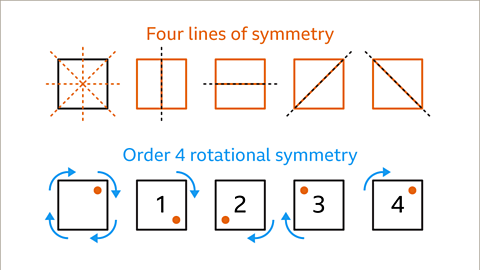
Image caption,
A square has four lines of symmetry. There are four ways the square can be cut into a pair of mirrored halves. Two lines of symmetry go through the midpoints of the opposite parallel sides and two go along the diagonals of the square. There are four ways in which the square can be cut into reflecting halves. A square has order 4 rotational symmetry, it will fit into its outline four times in a complete turn.
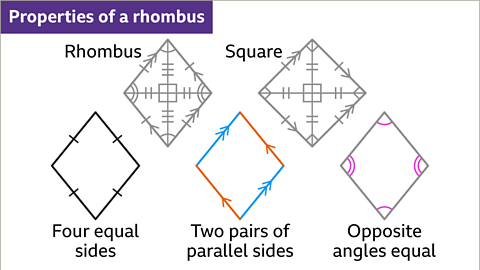
Image caption,
A rhombus has four sides equal in length. The opposite sides are parallel, meaning the rhombus has two pairs of parallel sides. Opposite angles are equal. When the angles are 90° the rhombus becomes a square.
Image caption,
The diagonals of a rhombus are perpendicular, they cross at right angles. When the diagonals of a rhombus are equal the rhombus becomes a square. The diagonals of a rhombus bisect each other.
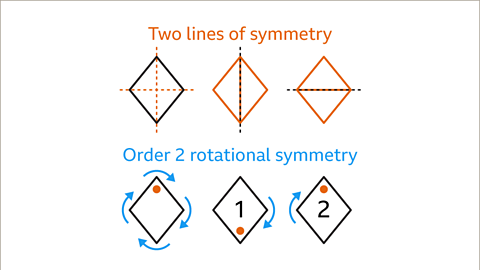
Image caption,
A rhombus has two lines of symmetry. There are two ways the rhombus can be cut into a pair of mirrored halves. The lines of symmetry follow the diagonals of the rhombus. A rhombus has rotational symmetry of order 2. It will fit into its outline twice in a full turn.
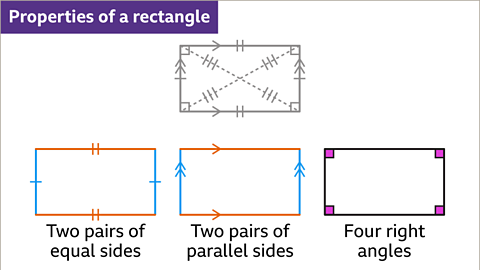
Image caption,
A rectangle has two pairs of equal parallel sides. When the sides are all equal the rectangle is a square. When the sides are not equal in length the rectangle is an oblong. The angles in a rectangle are all 90°.
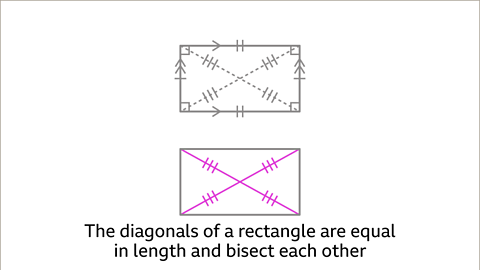
Image caption,
The diagonals of a rectangle are equal in length. They bisect each other.
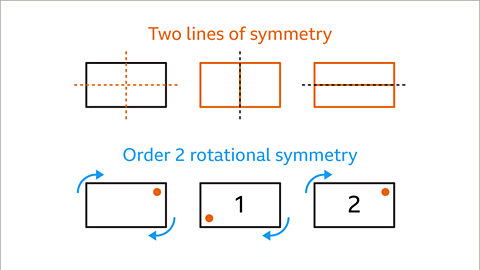
Image caption,
A rectangle has two lines of symmetry. There are two ways the rectangle can be cut into a pair of mirrored halves. The lines of symmetry pass through the midpoints of the opposite parallel sides. A rectangle has rotational symmetry of order 2. It fits into its outline twice in a full turn.

Question

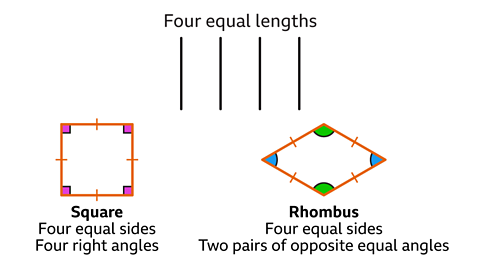
Name a polygon with four sides that are all equal in length.

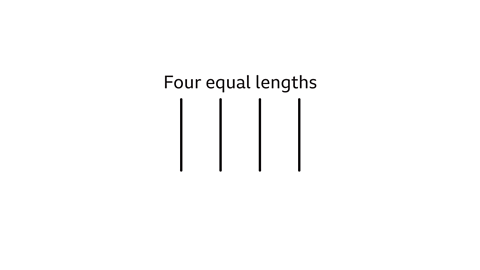
An image of four, spaced, vertical lines of the same length. Written above: four equal lengths.

Properties of parallelograms, kites and trapeziums

To classify a as a , or a , check for the following properties.

A parallelogram has:
- Two pairs of opposite sides that are equal in length.
- Two pairs of parallel sides
- Two pairs of equal opposite angles
- that each other.
- No reflection symmetry
- of 2
A kite has:
- Two pairs of sides that are equal in length.
- One pair of opposite equal angles.
- Diagonals that are unequal in length.
- One diagonal is bisected by the other.
- One line of symmetry.
- Rotational symmetry of order 1
A trapezium has:
- One pair of unequal parallel sides.
- Diagonals that are not equal in length.
- No reflection symmetry
- No rotational symmetry.
An isosceles trapezium has:
- One pair of unequal parallel sides.
- Two non-parallel equal sides.
- Two pairs of adjacent equal angles.
- Diagonals that are equal in length.
- One line of symmetry.
- No rotational symmetry.

Examples

Skip image gallery

Image caption,
Parallelograms, kites and trapeziums have four sides and four angles. The lengths and position of the edges help to identify the quadrilateral.
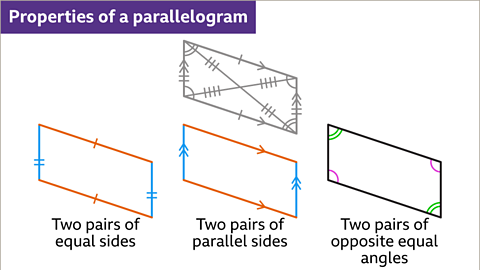
Image caption,
A parallelogram has two pairs of equal and parallel sides. When the lengths are equal the parallelogram is a rhombus. A parallelogram has two pairs of equal angles. The opposite angles in a parallelogram are equal. When the angles are 90° the parallelogram is a rectangle. When the sides are all equal and the angles are all 90° the parallelogram is a square.
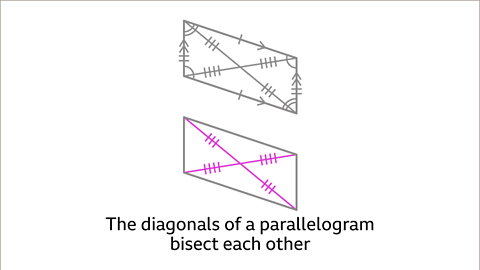
Image caption,
The diagonals of a parallelogram bisect each other. When the diagonals are equal in length the parallelogram is a rectangle.
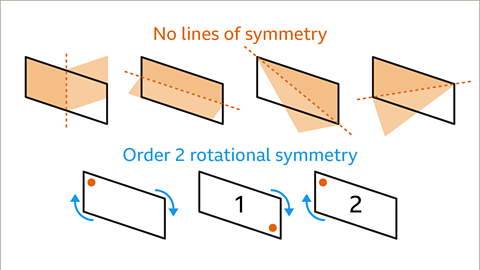
Image caption,
A parallelogram has no line symmetry. It is not possible to cut a parallelogram into two mirrored halves. A parallelogram has order 2 rotational symmetry and fits into its outline twice in a full turn.
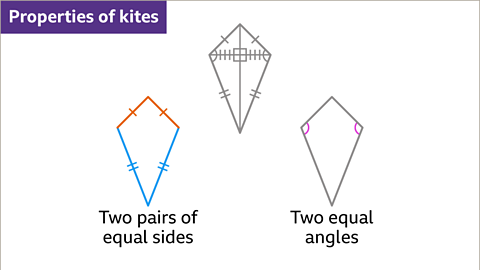
Image caption,
A kite has two pairs of equal adjacent sides. The equal sides are next to each other. When the sides are equal in length the kite is a rhombus. A kite has two equal angles.
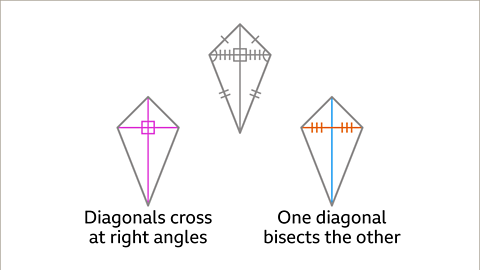
Image caption,
The diagonals of a kite are perpendicular, they cross at right angles. One of the diagonals is bisected by the other.
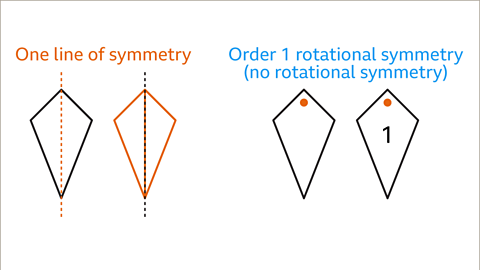
Image caption,
A kite has one line of symmetry. There is one way that a kite can be cut into a pair of mirrored halves. A kite has rotational symmetry of order 1, it only fits into its outline in one position. This means that a kite does not have rotational symmetry.
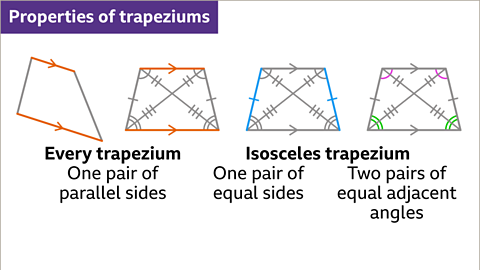
Image caption,
Every trapezium has one pair of unequal parallel sides. An isosceles trapezium also has two equal sides and two pairs of equal adjacent angles.
Image caption,
The diagonals of an isosceles trapezium are equal in length. This is not true for other trapeziums.
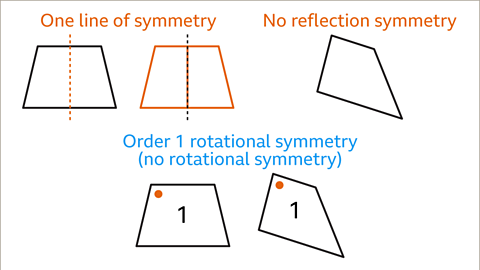
Image caption,
An isosceles trapezium has one line of symmetry. There is one way to cut the shape into a pair of mirrored halves. Trapeziums do not have line symmetry or rotational symmetry.

Questions

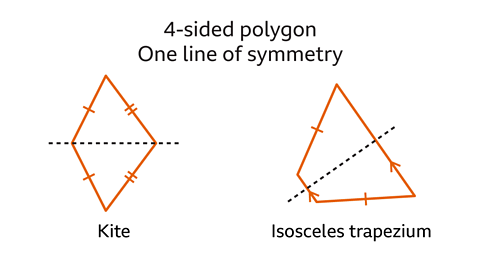
Question 1: Which quadrilaterals have exactly one line of symmetry?

The text: four sided polygon. One line of symmetry.

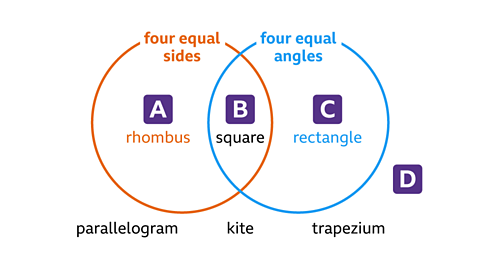
Question 2: On a copy of the Venn diagram, place the quadrilaterals square, rectangle, rhombus, parallelogram, kite and trapezium in the correct regions.

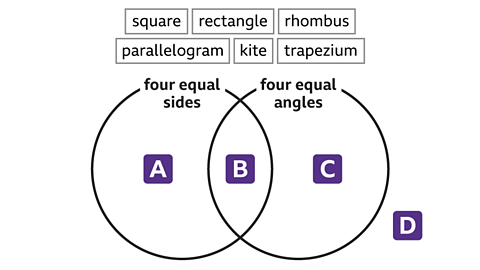
An image of a Venn diagram with two intersecting circles. The criteria for the circle on the left is labelled four equal sides. The criteria for the circle on the left is labelled four equal angles. Regions of the Venn diagram have been labelled. The circle on the left is labelled A. The intersection is labelled B. The circle on the right is labelled C and the outside is labelled D. Written above: square, rectangle, rhombus, parallelogram, kite, trapezium.

Identifying quadrilaterals by their properties

To identify a quadrilateral by a property, keep the following in mind.

Consider known facts:
- equal side lengths
- parallel sides
- equal angles
- diagonal properties
- reflection symmetry
- rotational symmetry

Remember: a property may apply to more than one quadrilateral.

Examples

Skip image gallery

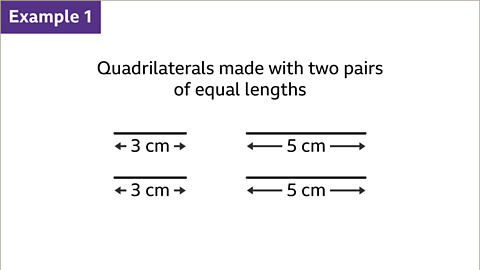
Image caption,
What quadrilaterals can be created from two lines that are 3 cm long and two lines that are 5 cm long?
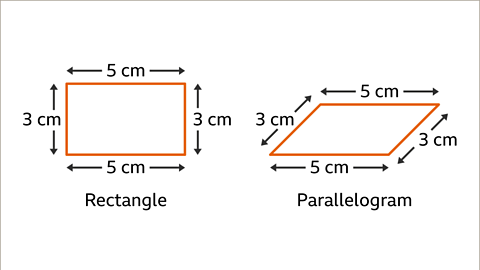
Image caption,
The quadrilaterals with two pairs of opposite equal lengths are a rectangle and a parallelogram. The rectangle and the parallelogram both have opposite equal sides. The rectangle and the parallelogram both have two pairs of parallel sides. The rectangle has 90° angles, the parallelogram has two pairs of equal opposite angles. There is another quadrilateral that can be formed.
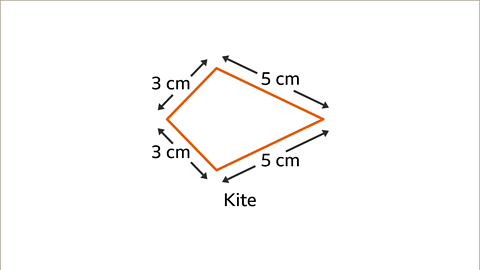
Image caption,
When the two equal lines are placed next to each other, the quadrilateral is a kite. A kite has two pairs of equal adjacent sides.
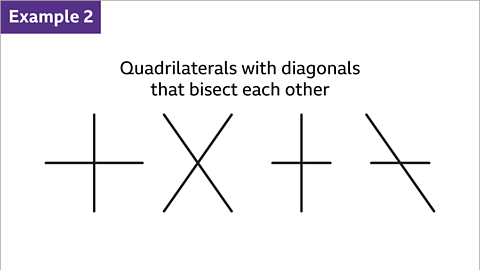
Image caption,
Work out which quadrilateral has diagonals that bisect each other.
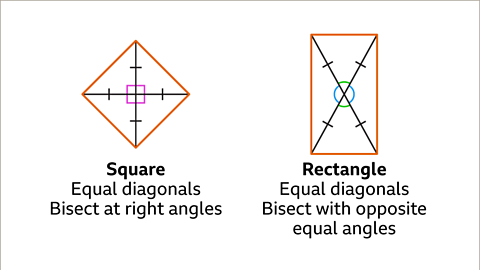
Image caption,
When the diagonal lengths are equal, the quadrilateral may be a square or a rectangle. The diagonals of a square bisect each other at right angles. The diagonals of a rectangle bisect each other. The angles where the diagonals cross are not right angles, the opposite angles are equal. There are other quadrilaterals whose diagonals bisect each other.
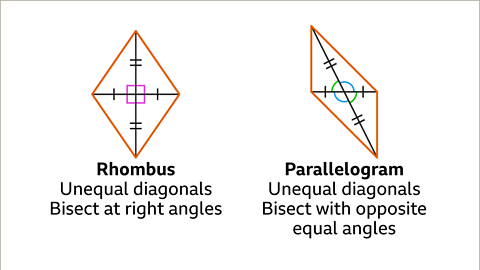
Image caption,
When the diagonal lengths are unequal, the quadrilateral may be a rhombus or a parallelogram. The diagonals of a rhombus are unequal and bisect each other at right angles. The diagonals of a parallelogram are unequal and bisect each other. The angles where the diagonals cross are not right angles, the opposite angles are equal.

Practise finding the properties of quadrilaterals

Practise working out properties of quadrilaterals with this quiz. You may need a pen and paper to help you with your answers.

Quiz

Real-life maths

An image of the surface of a basket. — Image caption,
A quadrilateral pattern can be seen in basket weave.

Properties of can be important in design. All quadrilaterals can tessellate. This means a single quadrilateral can be used to create a repeating pattern to cover a surface with no gaps. Geometric wallpaper and fabric designs often show tessellating patterns.

Quadrilaterals are used as the default shapes in all sorts of design software, including gaming, architecture, fashion and laser printing. A ‘basket weave’ design for use on fabric, wallpaper or even a web page is created by a series of rectangles, for example.