Key points
Any polygonA closed 2D shape bounded by straight lines. with three straight edges is a triangleA three-sided polygon..
A triangle is classified by the comparative length of its edgeSide of a polygon or a 3D shape. (sides) and by the size of its angles. These properties can be annotated on a diagram:
- hash marksShort lines marked on the side or edge of a shape. The same number of marks indicate equal lengths. are used to represent segments of equal length on diagrams.
- arcs (annotation)Curved marks inside the vertex of a shape. The same number of marks indicate angles are equal in size. at vertexThe point at which two or more lines intersect (cross or overlap). The corner of a shape. The plural form is vertices. are used to represent angles of equal measure.
- Other properties relate to the symmetry that the triangle has.
Understanding different types of angles and that angles in a triangle sum to 180° can be helpful when classifying a triangle.
Recognising line symmetry and rotational symmetry will also help.

Recognise equilateral, isosceles and scalene triangles
To interpret a diagram:
- Recognise that hash marksShort lines marked on the side or edge of a shape. The same number of marks indicate equal lengths. indicate equal lengths.
- Recognise that arcs (annotation)Curved marks inside the vertex of a shape. The same number of marks indicate angles are equal in size. in vertexThe point at which two or more lines intersect (cross or overlap). The corner of a shape. The plural form is vertices. can be used to indicate equal angles.
To classify a triangle using comparative lengths or angles:
- Look for any hash marks on the sides.
- The same number of hashes indicate equal lengths.
- Different numbers of hash marks indicate different lengths.
- Look for arcs inside each vertex.
- The same number of arcs indicate equal angles.
- Different numbers of arcs indicate different angles.
To identify the symmetry of a triangle:
- Count how many ways the triangle can be cut into a pair of mirrored halves. This gives the number of lines of symmetry of the triangle.
- Count how many ways the triangle will fit into its outline in a full turn (360°). This gives the order of rotational symmetry.
A unique set of properties relating to the comparative length of its sides and the comparative size of its angles help to identify equilateral triangleAll sides are equal in length. All angles are 60°., isosceles triangleTwo sides are equal in length. Two angles are the same size., and scalene triangleEach side is a different length. Each angle is a different size..
Examples

Image caption, Hash marks are used to show edges that are equal in length. The same number of hash marks shows lines that are equal in length.
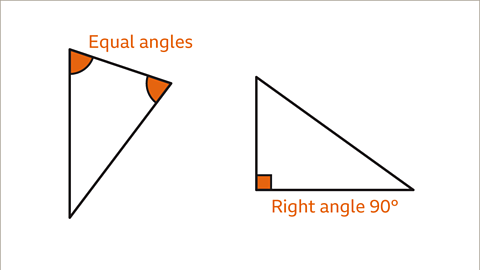
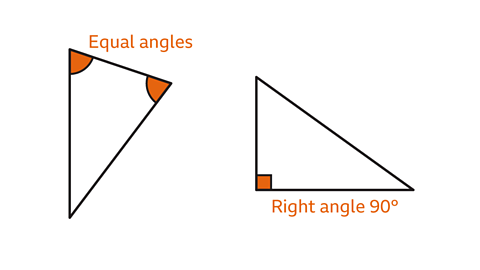
Image caption, Equal angles can be shown with arcs at a vertex. The same number of arcs means the angles are the same size. A square marked at a vertex shows an angle that is exactly 90°.
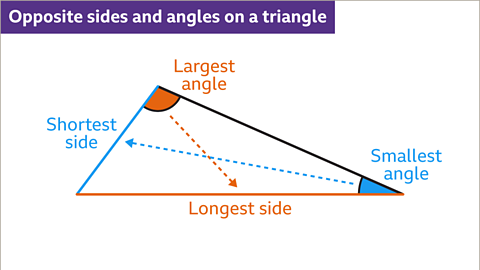
Image caption, The longest side of a triangle is opposite the largest angle. The shortest side of a triangle is opposite the smallest angle.
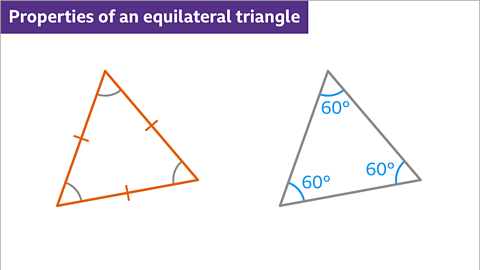
Image caption, All three sides of an equilateral triangle are the same length. The word equilateral means equal lines. Each angle is the same size. Each angle is 60°.
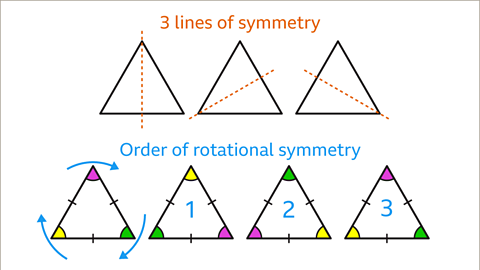
Image caption, An equilateral triangle has three lines of symmetry. There are three ways the triangle can be cut into a pair of mirrored halves. Each line of symmetry goes through a vertex and the midpoint of the opposite side. An equilateral triangle has rotational symmetry of order 3. An equilateral triangle fits into its outline three times in a full 360° turn.
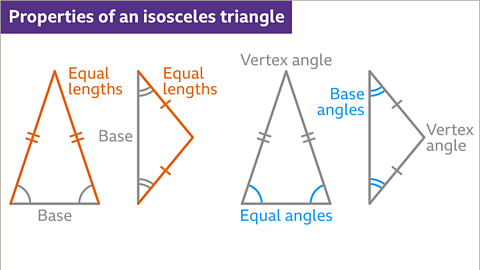
Image caption, An isosceles triangle has two sides that are equal in length. Isosceles means equal legs. The ‘legs’ are the two equal sides. The third side is called the base, even when the triangle is in a different orientation. An isosceles triangle has two angles that are the same size. These angles are referred to as the base angles even though the orientation of the triangle can mean they are not at the bottom of the diagram. The different angle is referred to as the vertex angle. The different angle is opposite the different side.
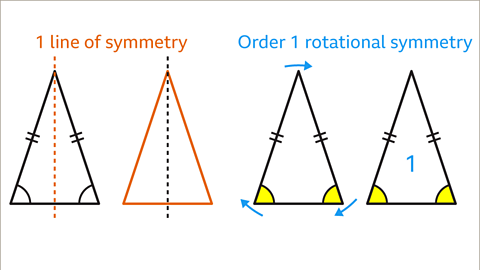
Image caption, An isosceles triangle has one line of symmetry. There is one way an isosceles triangle can be cut into a pair of mirrored halves. The line of symmetry goes through the vertex that has the different angle and the midpoint of the opposite (different length) side. An isosceles triangle has rotational symmetry of order 1. The triangle fits into its outline once in a full turn. An isosceles triangle does not have rotational symmetry.
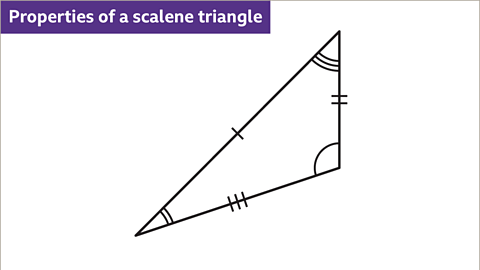
Image caption, A scalene triangle has sides that are all different lengths. Each angle in a scalene triangle is different.
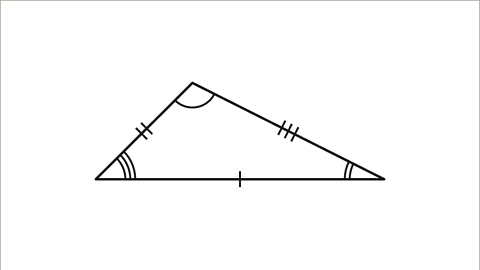
Image caption, A scalene triangle has no lines of symmetry and no rotational symmetry.
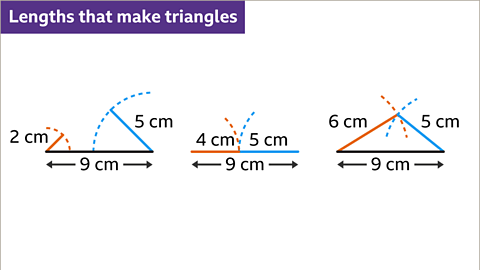
Image caption, Three lengths are needed to form a triangle. The total sum of the two shorter lengths must be greater than the longest length. Lengths of 2 cm, 5 cm and 9 cm do not make a triangle. The 2 cm and 5 cm lengths are too short. Lengths of 4 cm, 5 cm and 9 cm do not make a triangle, they create a straight line. Lengths of 6 cm, 5 cm and 9 cm do create a triangle as 6 + 5 > 9. The total length of the two shorter lines is greater than the length of the longest line.
1 of 10
Question
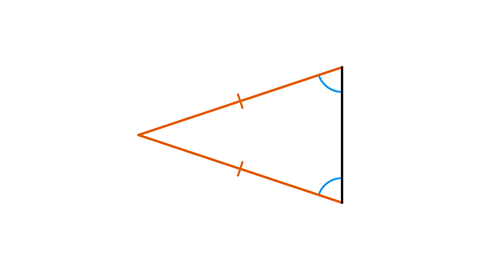
The triangle below is an isosceles triangle. Make a copy of the diagram on a piece of paper and mark on the correct annotation to show this.
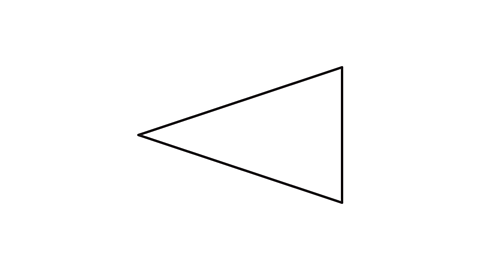
An isosceles triangle has two equal sides. One or more equal number(s) of hash lines on the equal sides are drawn on the diagram.
Two of the angles are equal. The equal angles are opposite the equal sides. They are marked with matching numbers of arcs to show that they are the same size.
Recognising acute-angled, right-angled, and obtuse-angled triangles
To classify a triangle using the specific size of its angles:
- Identify the type of angles in the triangle.
- Acute angles (less than 90°).
- Right angle (exactly 90°), marked with a square.
- Obtuse angles (greater than 90° and less than 180°).
- Using the combination of different types of angles, identify the triangle.
- An acute-angled triangle has three angles that are all less than 90°.
- A right-angled triangle has one angle that is exactly 90°.
- An obtuse-angled triangle has one angle that is greater than 90°.
The triangles can be further classified as equilateral triangleAll sides are equal in length. All angles are 60°., isosceles triangleTwo sides are equal in length. Two angles are the same size. or scalene triangleEach side is a different length. Each angle is a different size. by comparing the size of the angles. It is possible for each triangle described by its angle to have more than one classification.
Examples
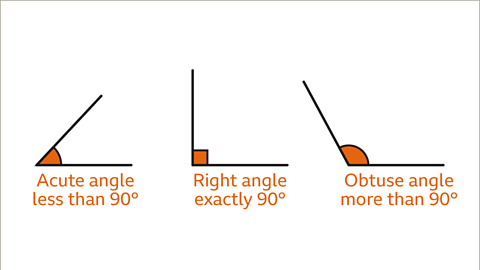
Image caption, A triangle may be described by the size of its angles, eg acute-angled, right-angled or obtuse-angled. An acute angle is less than 90°. A right angle is exactly 90°. An obtuse angle is greater than 90° and less than 180°, a straight line.
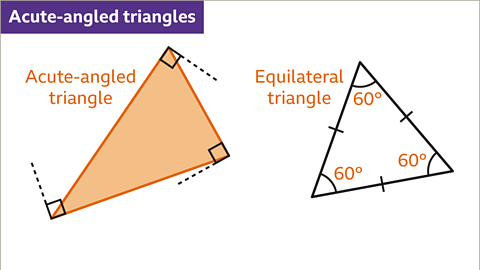
Image caption, The angles in an acute-angled triangle are all less than 90°. An equilateral triangle is an acute-angled triangle, all its angles are 60°.

Image caption, An isosceles triangle with all angles less than 90° is an acute-angled triangle. An isosceles triangle with angles of 50°, 50° and 80° is an acute-angled triangle.
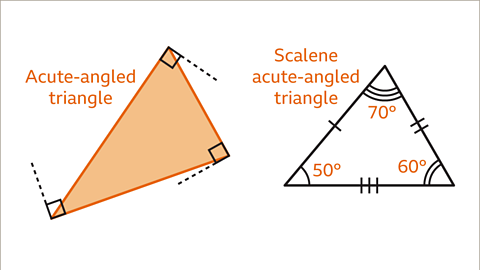
Image caption, A scalene triangle with all angles less than 90° is an acute-angled triangle. A scalene triangle with angles of 50°, 60° and 70° is an acute-angled triangle.
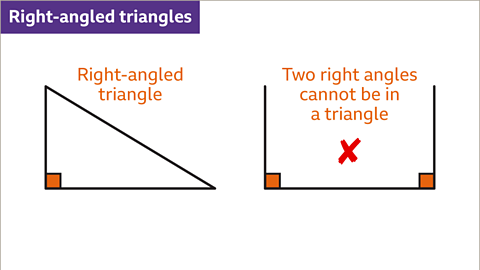
Image caption, A right-angled triangle contains one angle that is 90°. It is not possible to have more than one right angle in a triangle.
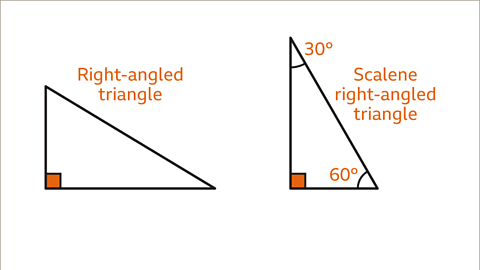
Image caption, A scalene triangle may be a right-angled triangle. A scalene triangle with angles 90°, 30° and 60° is a scalene right-angled triangle.
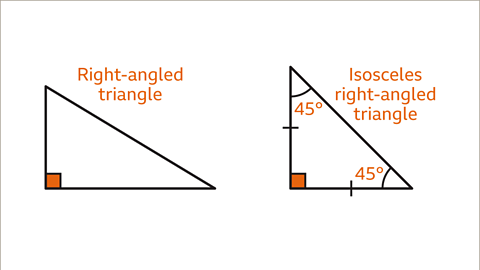
Image caption, An isosceles triangle with angles of 90°, 45° and 45° is a right-angled triangle. This is the only combination of angles that is possible. All right-angled isosceles triangles will have these same angles.
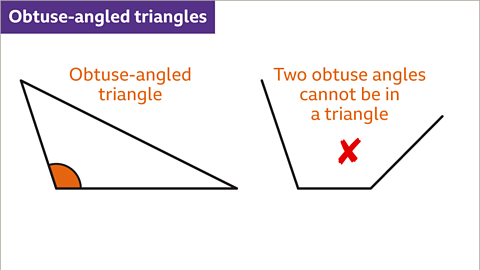
Image caption, An obtuse-angled triangle has one angle that is greater than 90° and less than 180°. It is not possible to draw a triangle with more than one obtuse angle.
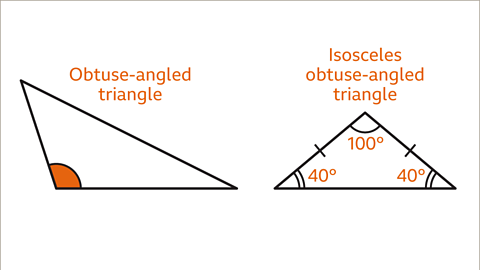
Image caption, An isosceles triangle with one angle greater than 90° is an obtuse-angled triangle. An isosceles triangle with angles of 100°, 40° and 40° is an obtuse-angled triangle.
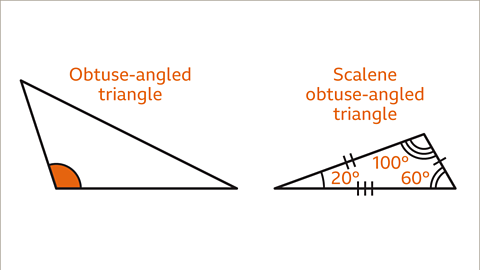
Image caption, A scalene triangle with one angle greater than 90° is an obtuse-angled triangle. A scalene triangle with angles of 100°, 20° and 60° is an obtuse-angled triangle.
1 of 10
Questions
Question 1: What type of triangle has angles of 35°, 65° and 80°?
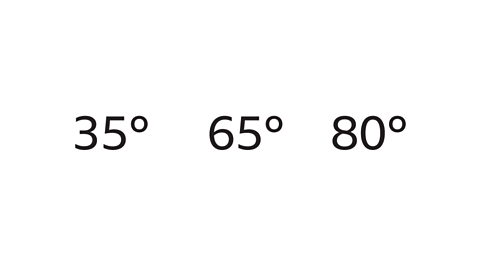
The three angles add up to 180°, so it is possible to draw a triangle.
Each angle is different, they are all less than 90°. The angles are inside a scalene triangle.
The angles are all acute angles.
The triangle is an acute-angled scalene triangle.

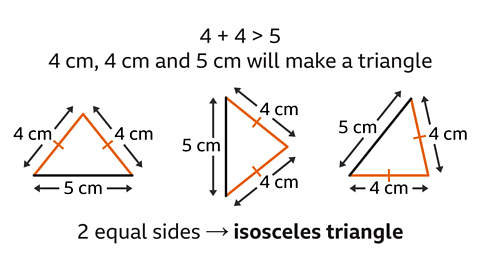
Question 2: What type of triangle has sides with lengths 4 cm, 5 cm and 4 cm?
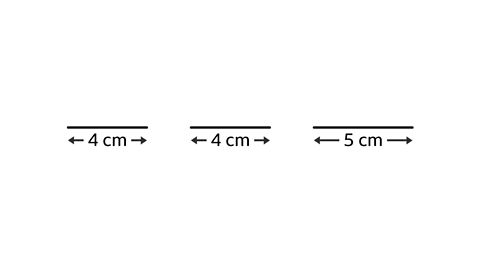
The two shorter sides have a total length that is greater than the longest side.
4 + 4 > 5
This means that a triangle can be drawn with the lengths 4 cm, 4 cm and 5 cm.
Two sides are the same length. The triangle is an isosceles triangle.
Practise working out properties of triangles
Practise working out properties of triangles with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

A triangle is a rigid shape. This fact is put to good use in constructing scaffolding. Separate lengths of iron pipework are fixed together with diagonals across any four-sided shapes.
This gives rigidity to the overall structure, which is essential for safety. This type of construction is also seen in bridges, cranes and mobile launcher platforms used for space rockets.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Shapes
Find out more by working through a topic
- count2 of 4
- count3 of 4

- count4 of 4