Key points

To understand symmetry a good understanding of shapes, including regular polygons and triangles, can be helpful.
There are two types of symmetry: reflective and rotational.
If a shape does not have symmetry it is called asymmetrical.

Reflective symmetry
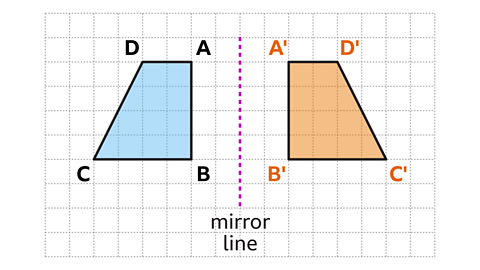
A line of symmetryAn imaginary line which splits a shape equally in two, where both sides are a reflection of each other. is an imaginary line which splits a shape equally in two.
Each half must be a mirror image of the other.
If a 2D shapeA flat shape. can be folded in half, with either side of the fold being a mirror image of the other, then it has a line of symmetry.
A mirror can be also used to help find lines of symmetry. When a mirror is placed in a position on a shape and the reflection matches the other half of the shape, then this is a line of symmetry.
Examples
Image caption, By exploring the different ways of folding a rectangle, we can work out the number of lines of symmetry.
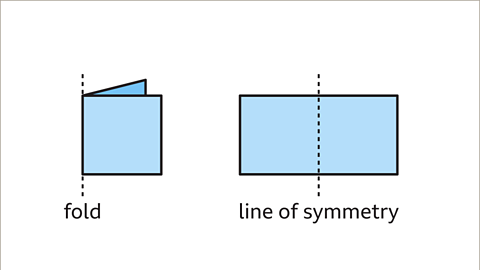
Image caption, The rectangle can be folded vertically down the middle. Both sides of the fold are the mirror image of each other. This fold is a line of symmetry.
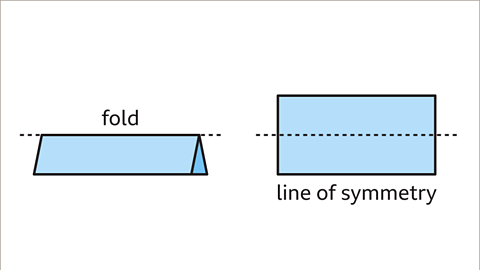
Image caption, The rectangle can also be folded horizontally down the middle. Both sides of the fold are the mirror image of each other. This fold is a line of symmetry.
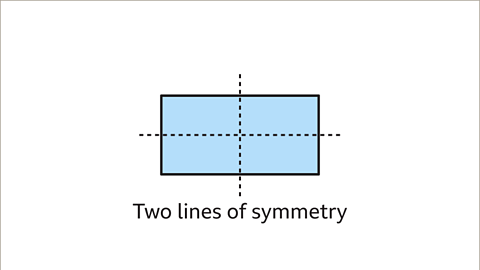
Image caption, In total, a rectangle has two lines of symmetry. It is not necessary to create a shape to check for lines of symmetry. The shape and its lines of symmetry could be sketched.
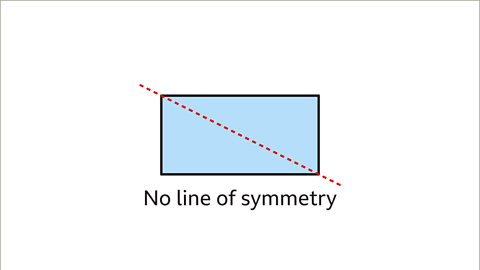
Image caption, Although the diagonal of a rectangle cuts the shape in half, it is not a line of symmetry.

Image caption, The fold shows the two sides are not the same. Using a mirror also confirms that the two halves are not identical.
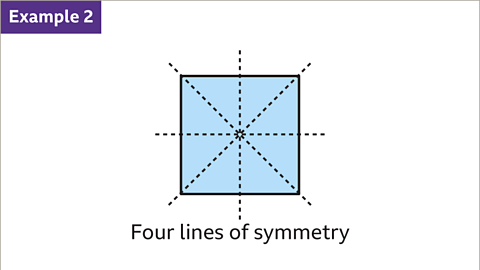
Image caption, A square has four lines of symmetry: one vertical, one horizontal and two across the diagonals.
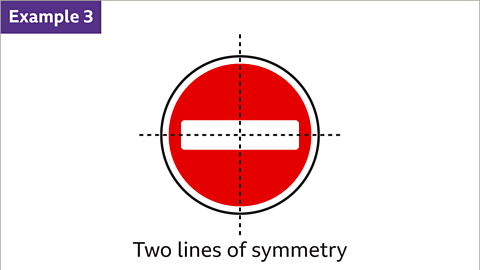
Image caption, Line symmetry doesn’t only apply to mathematical shapes. The no entry road sign has two lines of symmetry, one vertical and one horizontal.
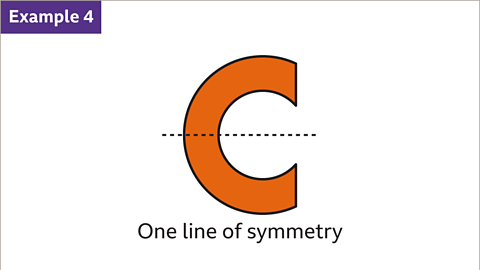
Image caption, The letter ‘C’ has one horizontal line of symmetry.
1 of 9
Question
How many lines of symmetry does an isosceles triangle have?
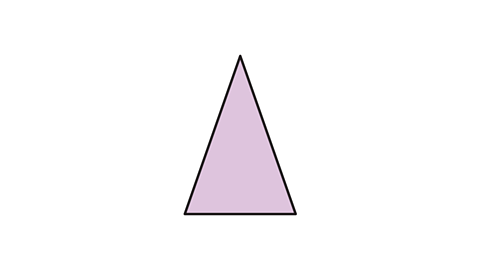
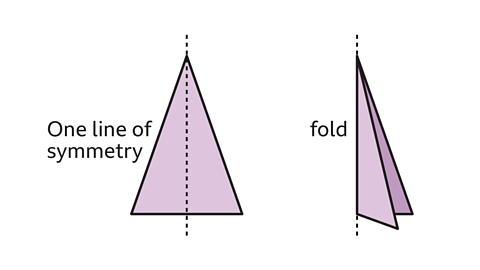
An isosceles triangle can only be folded vertically down the middle.
Both sides of the fold are the mirror image of each other. This fold is a line of symmetry.
Therefore, the isosceles triangle only has one line of symmetry.
Rotational symmetry
A shape has rotational symmetryA 2D shape has rotational symmetry about a point if it looks the same after a rotation through an angle greater than 0° and less than 360° about that point. if it looks the same in more than one position when the shape is rotated about its centre.
The number of times it looks the same through a full turn (360°) is called the order of rotational symmetry. For example, a shape that looks the same five times through a full turn has a rotational symmetry of order five.
To find the order of rotational symmetry:
- Choose a reference pointA place on a shape used to determine symmetrical properties and transformations of the shape. This can be decided by tracking the motion of the point. on the shape, usually a vertexThe point at which two or more lines intersect (cross or overlap). The corner of a shape. The plural form is vertices. (corner).
- Rotate the shape about its centre until the shape looks the same compared to its original starting position.
- Continue to rotate the shape, counting how many times it looks identical to its starting position, until the shape has been rotated a full turn (360°).
Examples
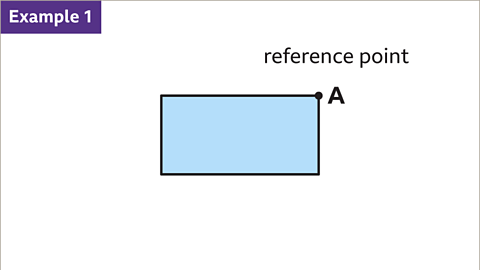
Image caption, To work out the order of rotational symmetry of a rectangle, pick a reference point and label it A.
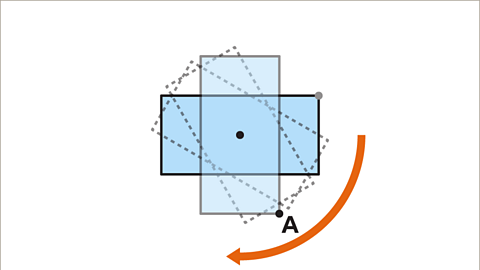
Image caption, Slowly rotate the shape clockwise about the centre, in the same direction as the hands on a clock. After a quarter turn (90°), reference point A is not in line with the original shape.
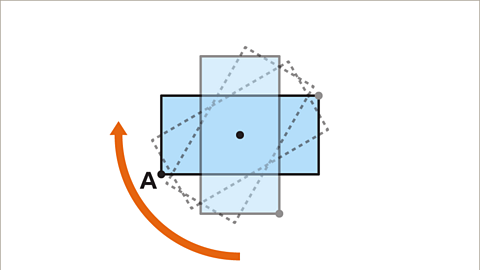
Image caption, After one half of a full turn (180°), reference point A is in line with the bottom left corner of the original shape. This is the first time the shapes look the same.
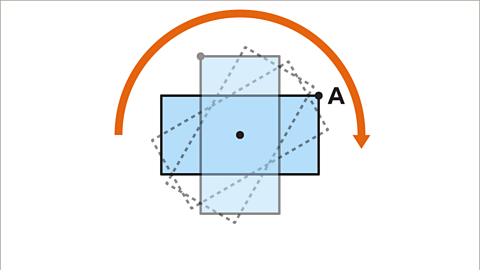
Image caption, After a further half of a turn (360° in total), the shape has returned to its original position. Reference point A is in line with the top right corner of the original shape. This is the second time the shapes look the same.
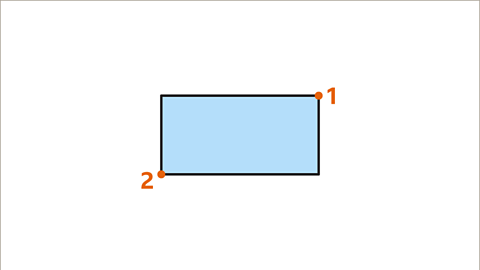
Image caption, The rectangle looked identical twice during the full turn, with reference point A at positions 1 and 2. The rectangle has rotational symmetry of order two.

Image caption, Symbols and logos often have rotational symmetry. To work out the order of rotational symmetry of this symbol, pick a reference point and label it A.

Image caption, After one third of a full turn (120°), the reference point A reaches position 1 where the shape looks the same as the original. After another third of a turn (120°), the reference point A reaches position 2 where the shape looks the same as the original. After the final third of a turn (120°), the reference point A reaches position 3 where the shape has returned to its original starting point. The recyclable symbol has rotational symmetry of order three.
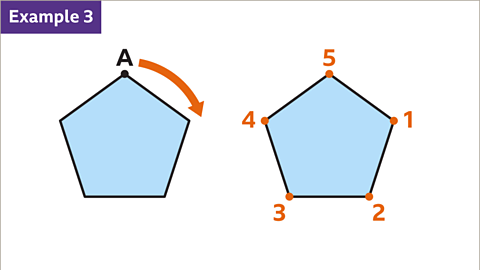
Image caption, A regular pentagon has rotational symmetry of order five. Through a full turn (360°) there are five positions where reference point A would make the shape look the same as the original.
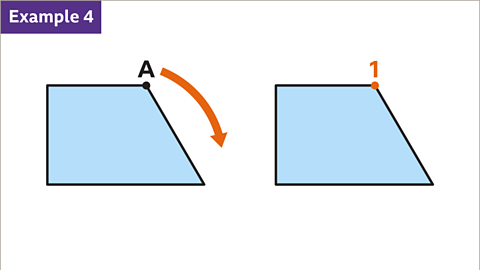
Image caption, Irregular shapes only look the same once through a full turn. There is only one position where reference point A would make the shape look the same as the original. Although this is called rotational symmetry of order one, the shape is described as having no rotational symmetry. Since this shape also has no line symmetry, it can be called asymmetrical.
1 of 9
Question
What is the order of rotational symmetry for an equilateral triangle?
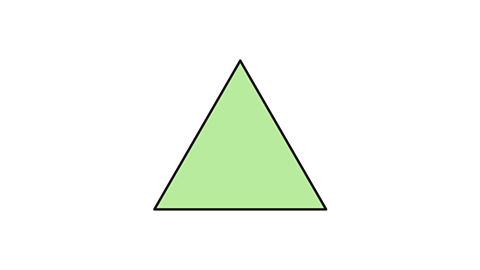

- Choose a reference point and label it A.
- Rotate the image around the centre.
- Through a full turn (360°) there are three positions where reference point A would make the shape look the same as the original.
- This means that the equilateral triangle has rotational symmetry of order three.
Symmetry in regular polygons
A regular polygon has sides which are all the same length and interior angles which are all equal size.
In a regular polygon, the number of lines of symmetry is the same as the number of sides.
The order of rotational symmetry is same as the number of sides.
Examples
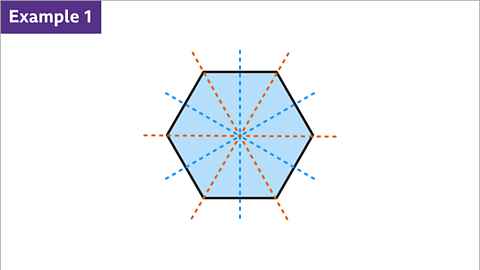
Image caption, A regular hexagon has six sides. A regular polygon has the same number of lines of symmetry as the number of sides. Therefore, a regular hexagon has six lines of symmetry. Three lines of symmetry pass through opposite vertices and three lines of symmetry pass through the mid-points of opposite sides.
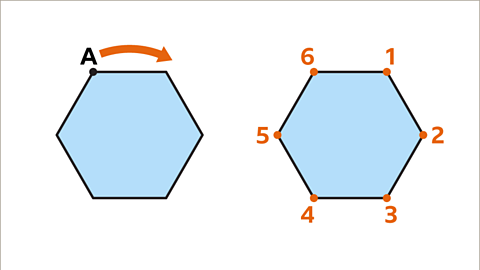
Image caption, A regular hexagon has rotational symmetry of order six. Through a full turn (360°), there are six positions where reference point A would make the shape look the same as the original.
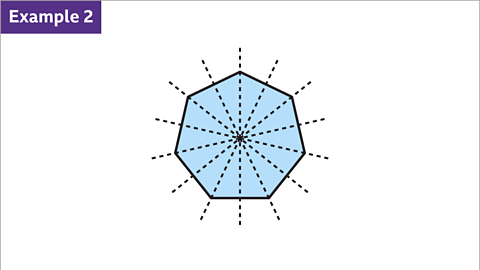
Image caption, A regular heptagon is a polygon with seven sides. Therefore, it has seven lines of symmetry. Each line of symmetry passes through a vertex (corner) to the midpoint of the opposite side.
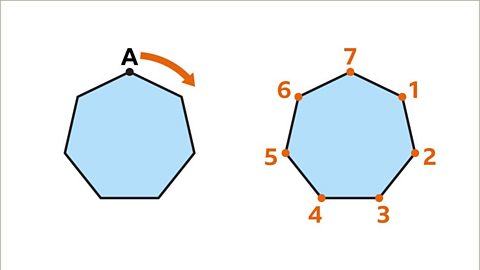
Image caption, The regular heptagon has rotational symmetry of order seven. Through a full turn (360°), there are seven positions where reference point A would make the shape look the same as the original.
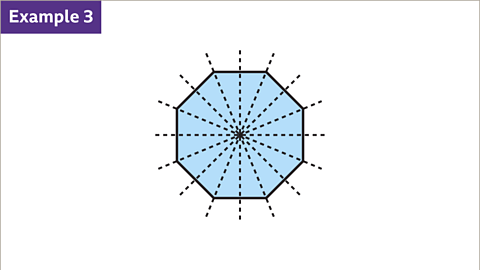
Image caption, A regular octagon is a polygon with eight sides. Therefore, it has eight lines of symmetry. Four lines of symmetry pass through opposite vertices and four lines of symmetry pass through the mid-points of opposite sides.
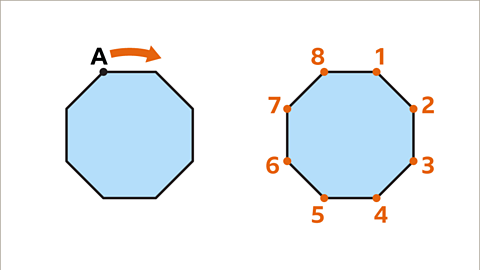
Image caption, The regular octagon has rotational symmetry of order eight. Through a full turn (360°), there are eight positions where reference point A would make the shape look the same as the original.
1 of 6
Question
How many lines of symmetry would a regular decagon, a 10-sided polygon, have?
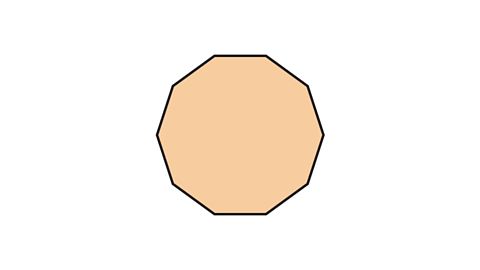
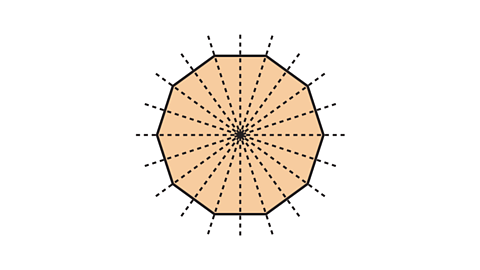
A regular decagon is a polygon with ten sides. Therefore, it has ten lines of symmetry.
Five lines of symmetry pass through opposite vertices and five lines of symmetry pass through the mid-points of opposite sides.
Practise identifying symmetry
Quiz
Practise identifying symmetry with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths

The London Eye is an example of a symmetrical structure.
It is 135 metres in height and has a diameter of 120 metres. 32 viewing capsules, which are also called pods, are equally spaced apart on the wheel. This means the structure has rotational symmetry of order 32.
The cables joining the edge of the wheel to the central point (known as the spindle) replicate the 32 lines of symmetry.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Symmetry and transformations
Find out more by working through a topic
- count2 of 6
- count3 of 6
- count4 of 6
- count5 of 6