Key points
When transforming a shape, either through translation, reflection or rotation, a congruent shape is produced. Enlargements create shapes that are similar.
When two shapes are the same in shape and size, they are congruentTwo shapes that are identical. shapes. When two shapes are different in size but proportionally the same shape, they are similar shapesOne shape is an enlargement of another. The angles in each shape are the same, and the side lengths are in the same proportion. All squares are mathematically similar. All circles are mathematically similar. shapes.
To understand congruence and similarity, a good understanding of the properties of polygons, including triangles and quadrilaterals, can be helpful.

Congruent shapes
Two shapes are described as congruentTwo shapes that are identical. if they are identical.
- The lengths of sides (edges) and sizes of angles must be equal between the two shapes for them to be congruent.
- reflectionA reflection is a mirror image of the shape. An image will reflect through a line, known as the line of reflection. or rotationA transformation of a shape which results in a turning effect on the shape. change the orientation of a shape but they are still congruent to the original shape.
- A great way to check if two shapes are congruent is to place one on top of the other. If they match, with no overlaps, they are congruent.
Examples
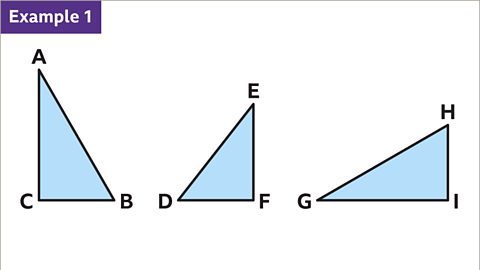
Image caption, Two of these triangles are congruent, which means they are identical in shape and size.
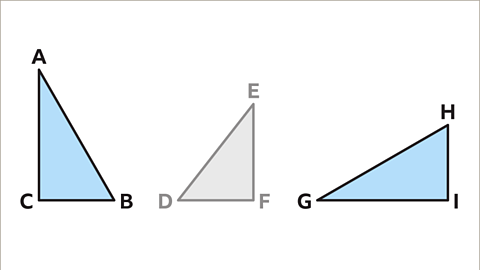
Image caption, Triangles ABC and GHI are congruent. Triangle GHI is the same as ABC but has been rotated 90° anticlockwise. Triangle DEF is a different size.
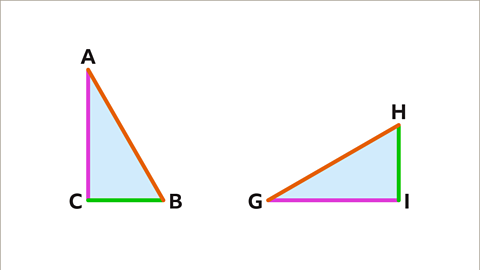
Image caption, Line segments AB and GH are the same length. BC and HI are the same length. AC and GI are the same length.
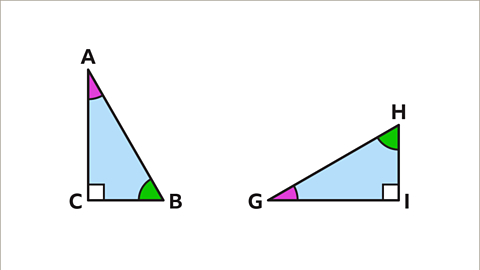
Image caption, Angle A and angle G are equal. Angle B and angle H are equal. Angle C and I are equal and are both right angles.
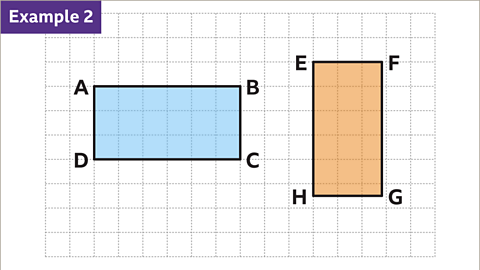
Image caption, These two rectangles are not congruent.
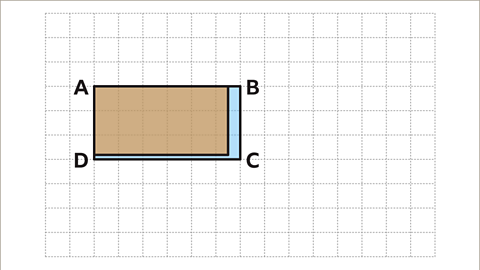
Image caption, Rotating rectangle EFGH and placing it on top of rectangle ABCD shows they are not the same size.
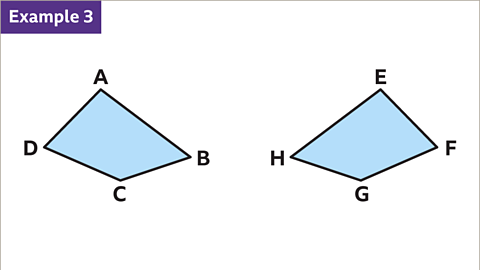
Image caption, These two quadrilaterals are congruent.
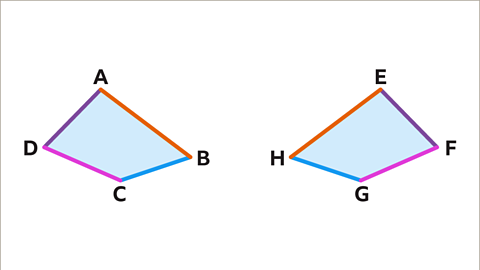
Image caption, EFGH is a reflection of ABCD on a vertical mirror line. Line segments AB and EH are the same length. They correspond to each other, which means they are in the same place in two different shapes. BC and GH are the same length. CD and FG are the same length. AD and EF are the same length.
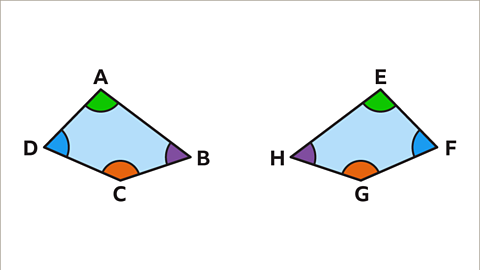
Image caption, Angles in congruent shapes are equal. Angle A and angle E are equal. They correspond to each other. Angle B and angle H are equal. Angle C and G are equal. Angle D and F are equal.
1 of 9
Question
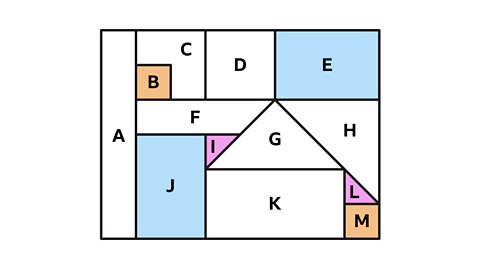
Look at the grid of shapes. How many congruent pairs can you find?
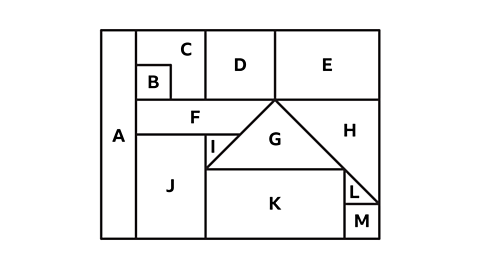
Two shapes are described as congruent if they are identical.
Shapes B and M are congruent squares.
Shapes E and J are congruent rectangles. When E is rotated 90° clockwise it has the same orientation as J.
Shapes I and L are congruent triangles. When I is rotated 90° anti-clockwise it has the same orientation as L.
Similar shapes
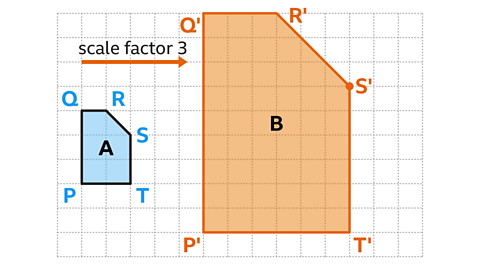
Two shapes are described as similar shapesOne shape is an enlargement of another. The angles in each shape are the same, and the side lengths are in the same proportion. All squares are mathematically similar. All circles are mathematically similar. if one is an enlargementA transformation of a shape which results in a shape increasing or decreasing in size. of the other. The shapes do not need to be orientationThe position of a shape in relation to a coordinate system. Orientation is the way an object is angled. the same way.
The sizes of angles must be equal between the two shapes.
The shapes must also be proportionalityA relationship that is maintained between numbers. the same. If one side on the enlarged shape doubles in length, all sides must be double the original size shape. The increase in size from one shape to another is called a scale factorThe ratio between corresponding sides in an enlargement..
The shapes may need to be rotationA transformation of a shape which results in a turning effect on the shape. to find out if they are similar.
It is possible to calculate missing lengths on similar shapes when given either the scale factor or enough information to calculate it.
Examples
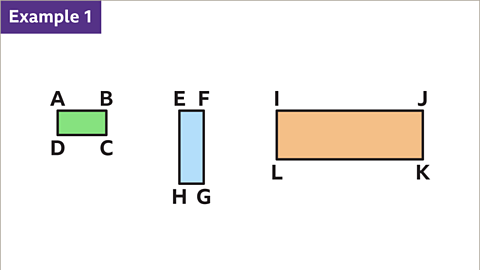
Image caption, All of these rectangles are different sizes, but two are proportionally the same and similar.
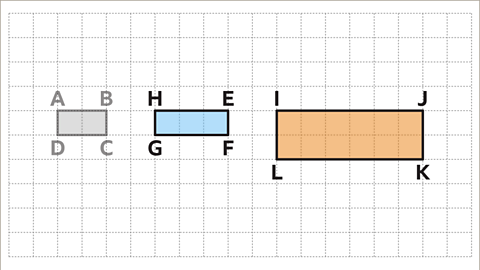
Image caption, Rotating rectangle EFGH makes it easier to visualise which two shapes are similar. Rectangles EFGH and IJKL are similar. Their lengths are three times their widths. ABCD is too short in length to be similar.
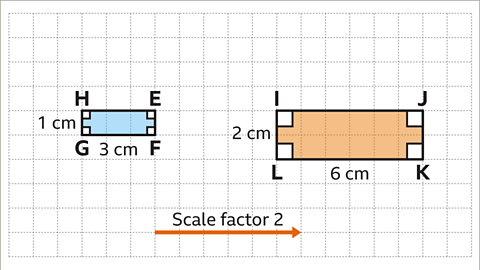
Image caption, Rectangle IJKL is an enlargement by scale factor two. All dimensions have doubled in length. Line EF is 1 cm and line IL is 2 cm. Line EH is 3 cm and line KL is 6 cm. This means EFGH is half the scale of IJKL. All the angles are the same (90°).
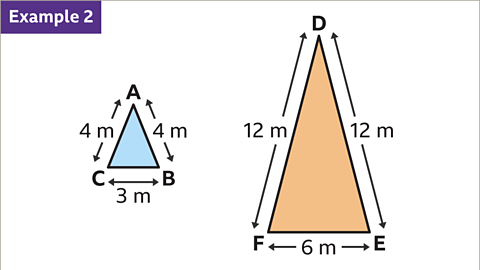
Image caption, Isosceles triangles ABC and DEF are not proportionality the same. The base in EF is twice the size as BC. EF ÷ BC = 6 ÷ 3 = 2. The sides DE and DF are three times the size AB and AC. DF ÷ AC = 12 ÷ 4 = 3. This means triangles ABC and DEF are not similar.
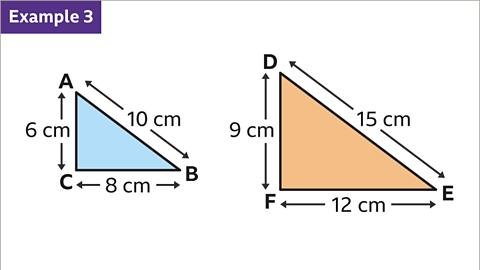
Image caption, Triangles ABC and DEF are similar. There is enough information to work out the scale factor.
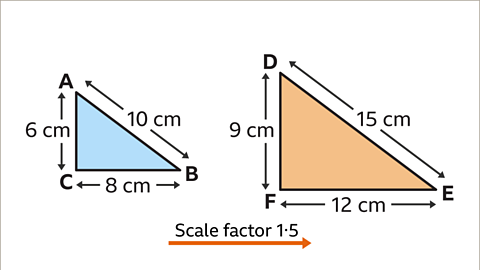
Image caption, By comparing any pair of corresponding sides, eg DE and AB, the scale factor can be calculated. Scale factor = DE/AB. Scale factor = 15/10. Scale factor = 1·5. Triangle DEF is an enlargement by scale factor 1·5
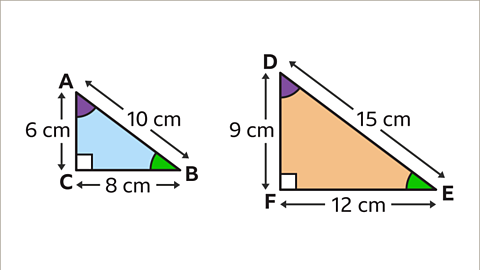
Image caption, Angle A and angle D are equal. Angle B and angle E are equal. Angle C and F are equal and are both right angles.
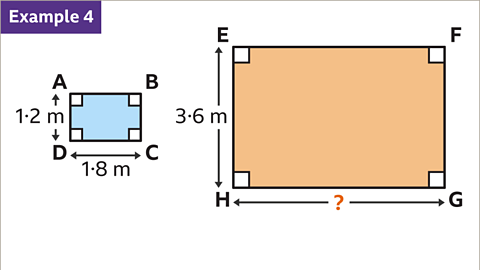
Image caption, Rectangles ABCD and EFGH are similar. Rectangle EFGH is an enlargement scale factor 3. Calculate the length of GH.
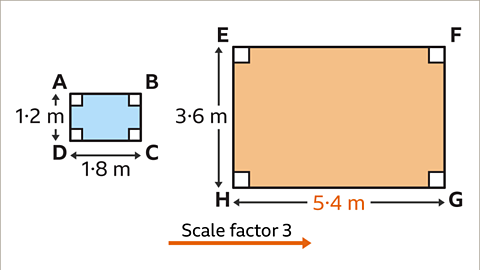
Image caption, All dimensions have multiplied by 3. GH = CD × 3. GH= 1·8 × 3. GH = 5·4 m.
1 of 9
Question
Which of these two triangles are similar?
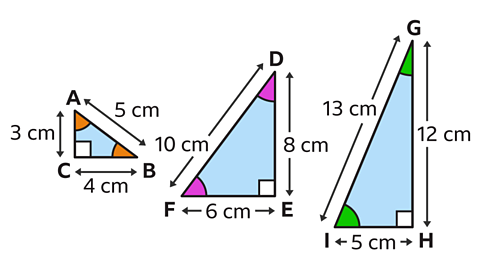
Rotating triangles into the same orientation, with the right-angle in the bottom right, makes it easier to visualise which two shapes are similar.
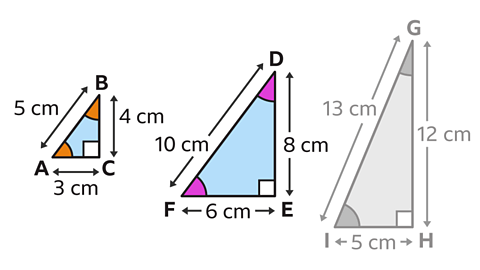
Triangles ABC and DEF are similar.
Triangle DEF is an enlargement scale factor 2.
Line segment EF corresponds to AC.
EF = AC × 2
EF = 3 × 2
EF = 6 cm.
Similarly, line segment DE corresponds to BC.
DE = BC × 2
DE = 4 × 2
DE = 8 cm.
Practise working with congruent and similar shapes
Quiz
Practise working with congruent and similar shapes with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths

Some congruent shapes can fit together without gaps. If this is possible the shape is said to tessellate.
The construction of a beehive is a real-life example of a tessellation pattern.
The hexagon shapes fit together to form the structure. The bees use this pattern as it is an efficient use of the space which involves as little wax, the material which they use, as possible.
Similar tessellation patterns can be found in the way paths, driveways and brick walls are designed.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Symmetry and transformations
Find out more by working through a topic
- count3 of 6
- count4 of 6
- count5 of 6
- count6 of 6