Key points
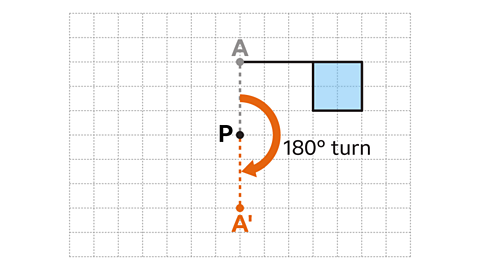
An enlargementA transformation of a shape which results in a shape increasing or decreasing in size. is a type of transformationA change in position or size, transformations include translations, reflections, rotations and enlargements..
An enlargement increases or decreases the size of the shape (objectThe starting shape prior to a transformation.). The new shape (imageThe resultant position of a shape after a transformation.) is a similar shape.
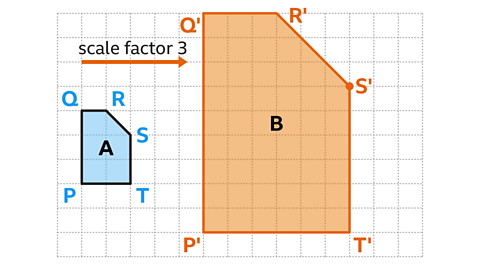
The increase in size from one shape to another is called a scale factorThe ratio between corresponding sides in an enlargement..
The position of the enlarged shape is determined by a point called the centre of enlargementA point which defines the position of an enlarged shape..
- If a vertexThe point at which two or more lines intersect (cross or overlap). The corner of a shape. The plural form is vertices. and the centre of enlargement share the same point, that point will be invariantA vertex or line segment that does not change after a transformation. under the enlargement.
When enlarging shapes, a good understanding of similar shapes and naming and plotting coordinates can be helpful.

Scale factors
When a shape is enlarged, the length of each side is multiplied by the same value. This value is called the scale factorFor two similar geometric figures, the ratio of corresponding edge lengths..
For example, to enlarge a shape with the scale factor of two, the length of all sides would be multiplied by two. Since the new shape is similar, all of the angles would be the same size.
A scale factor greater than one produces a larger shape. A scale factor between zero and one results in a smaller shape.
When given two shapes, a scale factor can be worked out by dividing corresponding sides.
Examples
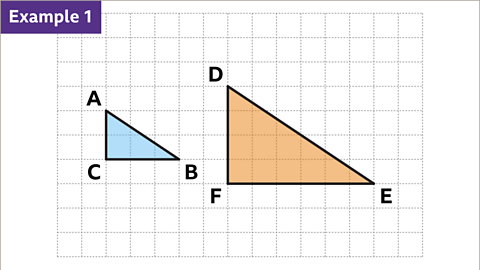
Image caption, Triangle DEF is an enlargement of triangle ABC.
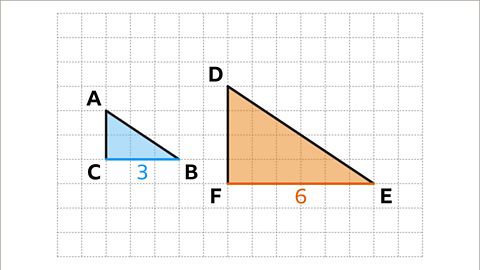
Image caption, The scale factor can be calculated by dividing a pair of corresponding sides. For example, in these shapes EF and BC are corresponding sides. BC has a length of three squares and EF has a length of six squares.
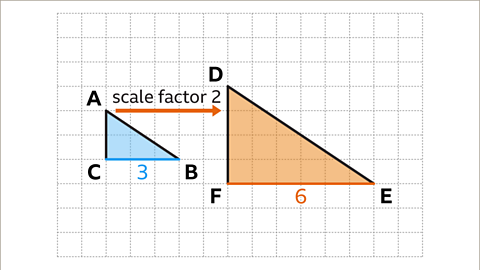
Image caption, Scale factor = EF/BC = 6⁄3 = 2. Therefore, triangle DEF is an enlargement of triangle ABC by a scale factor of 2
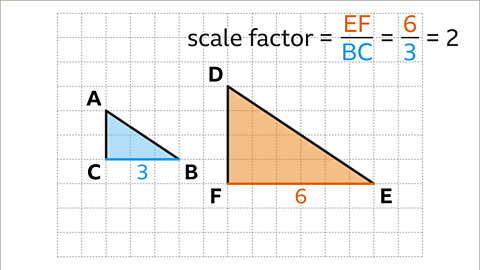
Image caption, The scale factor of triangle ABC compared to triangle DEF can be described in a similar way. This time the sides need to be divided in the opposite order.
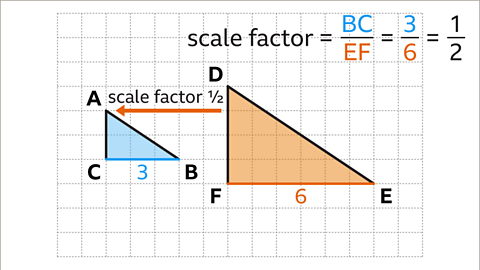
Image caption, Scale factor = BC/EF = 3⁄6 = 1⁄2. Therefore, triangle ABC is an enlargement of triangle DEF by a scale factor of ½
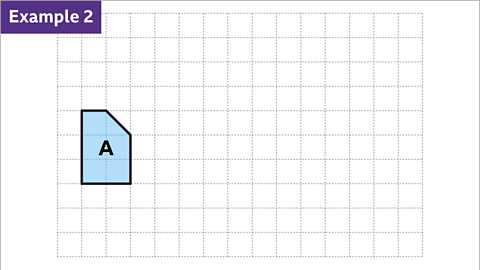
Image caption, Shape B is an enlargement of shape A by a scale factor of three. Therefore, all lengths on shape B need to be drawn three times the size.
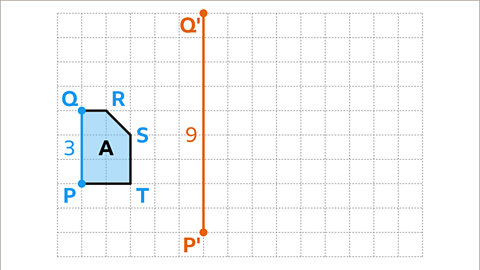
Image caption, Label the vertices of shape A. In shape A, the vertical line PQ has a length of three squares. Multiply the length of the vertical line by the scale factor of three. 3 × 3 = 9. Shape B has a corresponding side P'Q' with length of nine squares.
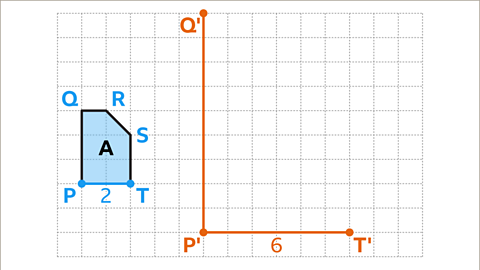
Image caption, The horizontal line PT has a length of two squares. Multiply the length of the horizontal line by the scale factor of three. 2 × 3 = 6. Shape B has a corresponding side P'T' with a length of six squares.
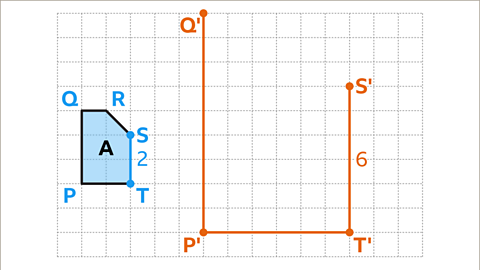
Image caption, The vertical line ST has length of two squares. Multiply the length of the vertical line by the scale factor of three. 2 × 3 = 6. Shape B has a corresponding side S'T' with a length of six squares.
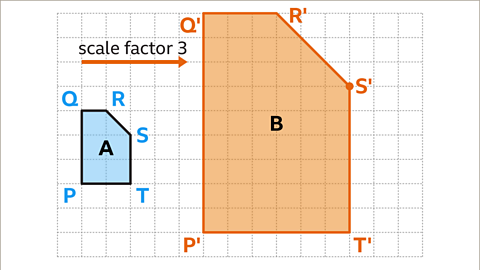
Image caption, Continue this process for the final two line segments, QR and RS. The horizontal line QR has length of one square. Multiply the length of QR by the scale factor of three. 1 × 3 = 3. Shape B has a corresponding side Q'R' with a length of three squares. The final side R’S’ can now be drawn to complete the shape. The shape is complete. Shape B is an enlargement of shape A by a scale factor of three.
1 of 10
Question
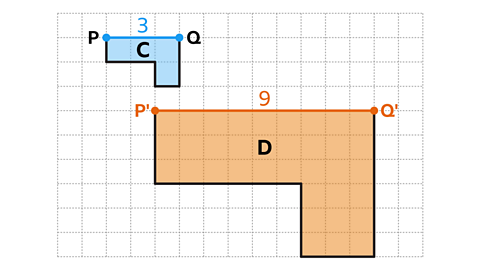
Shape D is an enlargement of shape C. What is the scale factor that takes shape C to shape D?
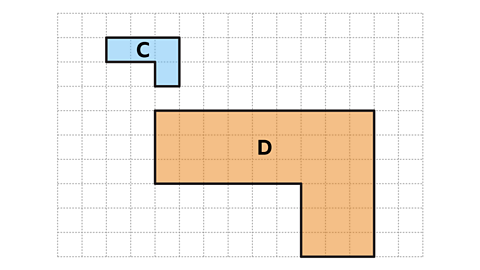
- The scale factor can be calculated by dividing a pair of corresponding sides.
- Using the horizontal line segment labelled PQ in shape C, PQ has length three squares. The corresponding line segment P'Q' in shape D is nine squares long.
- Scale factor = \( \frac{PQ}{P'Q'} \) = \( \frac{9}{3} \) = 3
- Shape D is an enlargement of shape C by a scale factor of three.
Enlarging by an integer scale factor
Enlarging by a positive integerIntegers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, 8, and 10000 are examples of integers. scale factor increases the size of the shape. When using a centre of enlargement, the final position of the new shape can be determined.
To work out the position of the image after an enlargement:
- Pick a vertexThe point at which two or more lines intersect (cross or overlap). The corner of a shape. The plural form is vertices. on the shape (object).
- Count the distance between the centre of enlargement and the vertex. This can be broken down into horizontalThe right-left direction on a graph or map. Parallel to the horizon. and verticalA line that is perpendicular to the horizon.displacementA change in position of a shape..
- Multiply these displacements by the scale factor.
- Using these values, count from the centre of enlargement to find the position of the corresponding vertex.
- Repeat the process for additional vertices.
The answer can be checked by drawing lines through corresponding points on the object and image. These will meet at the centre of enlargement.
Examples
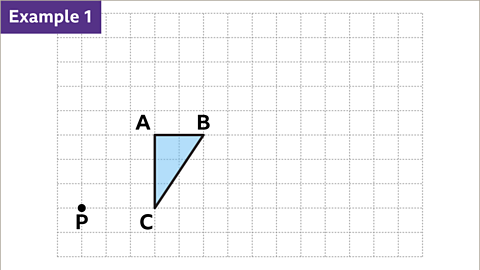
Image caption, Triangle ABC is to be enlarged by a scale factor of two, using point P as the centre of enlargement.
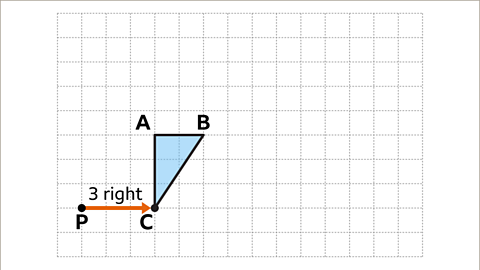
Image caption, Starting with vertex C, the vertex is three squares to the right of the centre of enlargement.
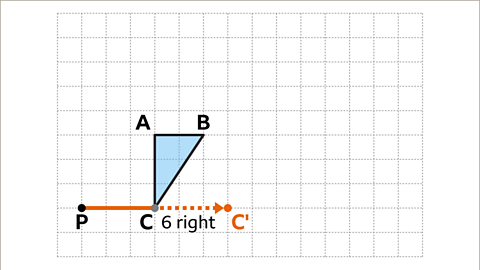
Image caption, Multiply this displacement by the scale factor of two. 2 × 3 = 6. The corresponding point C' needs to be six squares to the right of the centre of enlargement.
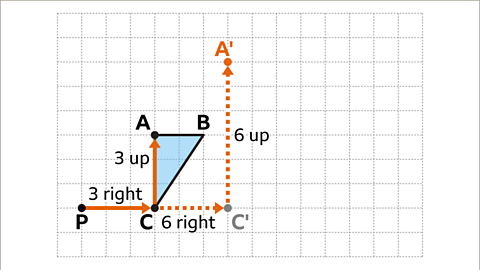
Image caption, Vertex A is three squares to the right and three squares up from the centre of enlargement. Multiply this displacement by the scale factor of two. 3 × 2 = 6. The corresponding point A' needs to be six squares to the right and six squares up from the centre of enlargement.
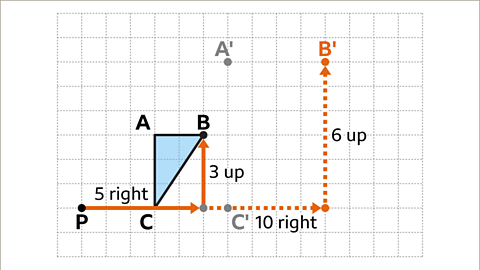
Image caption, Vertex B is five squares to the right and three squares up from the centre of enlargement. Multiply this displacement by the scale factor of two. 5 × 2 = 10 and 3 × 2 = 6. The corresponding point B' needs to be ten squares to the right and six squares up, from the centre of enlargement.
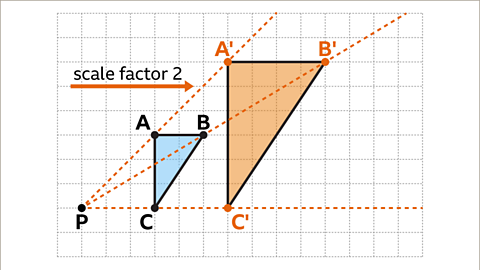
Image caption, Draw lines to connect each new vertex to draw the enlarged shape. The enlargement of the shape is complete. Shape A'B'C' is an enlargement of ABC by a scale factor of two, with point P as the centre of enlargement. The answer can be checked by drawing dashed lines through pairs of corresponding points. These lines all meet at the centre of enlargement, point P.
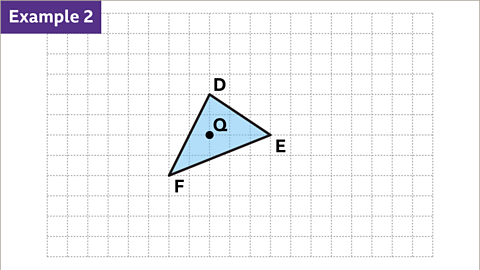
Image caption, It is possible to enlarge a shape where the centre of enlargement is inside the shape. Triangle DEF is to be enlarged by a scale factor of three, with point Q as the centre of enlargement.
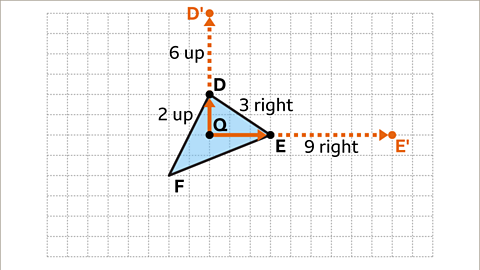
Image caption, Vertex D is two squares up from the centre of enlargement. Multiply this displacement by the scale factor of three. 2 × 3 = 6. The corresponding point D' needs to be six squares up from the centre of enlargement. Vertex E is three squares to the right of the centre of enlargement. Multiply this displacement by the scale factor of three. 3 × 3 = 9. The corresponding point E' needs to be nine squares to the right of the centre of enlargement.
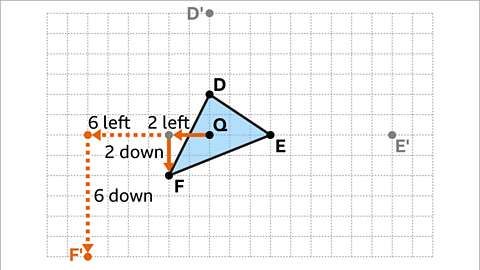
Image caption, Vertex F is two squares to the left and two squares down from the centre of enlargement. Multiply this displacement by the scale factor of three. 2 × 3 = 6 and 2 × 3 = 6. The corresponding point F' needs to be six squares to the left and six squares down from the centre of enlargement.

Image caption, Draw a line to connect each new vertex. The enlargement of the shape is complete. Shape D'E'F' is an enlargement of DEF by a scale factor of three, with point Q as the centre of enlargement. The answer can be checked by drawing dashed lines through pairs of corresponding points. These lines all meet at the centre of enlargement, point Q.
1 of 10
Question
Shape EFGH is an enlargement of shape ABCD. It has been enlarged using a scale factor of two, with point P as the centre of enlargement.
One vertex on the enlarged shape EFGH is in the wrong position. Which is the incorrect vertex?
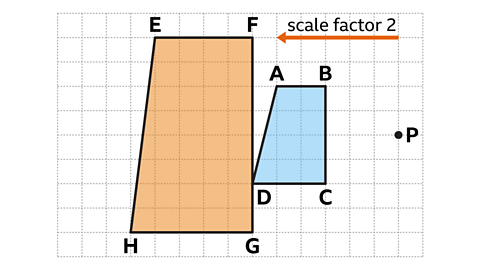
- Vertex H is the incorrect vertex
- The answer can be checked by drawing dashed lines through pairs of corresponding points.
- These lines should all meet at the centre of enlargement, point P.
- The line through H and D does not intersect with P, so vertex H is incorrect.
- This could also be checked using the scale factor of two. In the enlarged shape, GH should be double the length of CD.
GH = CD × 2
GH = 3 × 2
GH = 6
- Line segment GH is only five squares long. The correct position for H is one square further to the left.
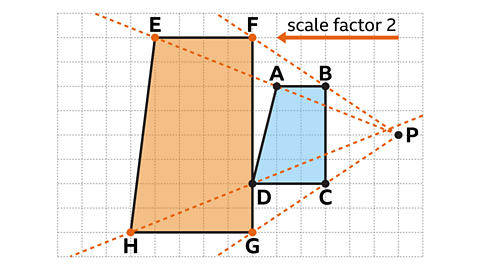
Enlarging by a fractional scale factor
Enlarging by a fractional scale factorA scale factor larger than zero but smaller than one. decreases the size of the shape.
To enlarge a shape by a fractional scale factor, the same method as enlarging by an integer scale factor can be used.
Multiplying the displacements by a fraction will result in a smaller distance between the centre of enlargement and a corresponding vertex.
Examples

Image caption, Shapes can be enlarged on sets of axes. Enlarge triangle ABC by a scale factor ⅓. Use point P with the coordinates of (1, 10) as the centre of enlargement.
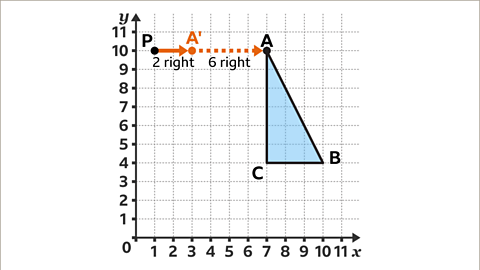
Image caption, Start with vertex A. The vertex is six squares to the right of the centre of enlargement. Multiply this displacement by the scale factor of a ⅓. 6 × ⅓ = 2. The corresponding point A' needs to be two squares to the right of the centre of enlargement.
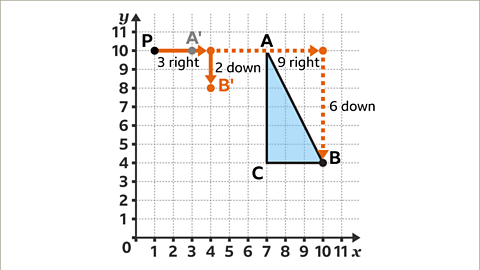
Image caption, Vertex B is nine squares to the right and six squares below the centre of enlargement. Multiply this displacement by the scale factor of a ⅓. 9 × ⅓ = 3 and 6 × ⅓ = 2. The corresponding point B' needs to be three squares to the right and two squares below the centre of enlargement.
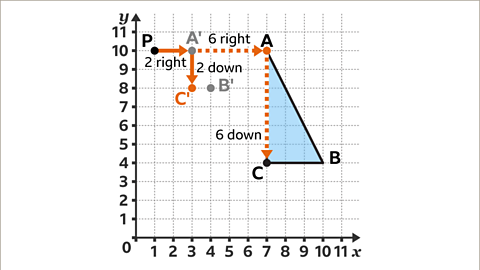
Image caption, Vertex C is six squares to the right and six squares below the centre of enlargement. Multiply this displacement by the scale factor of a ⅓. 6 × ⅓ = 2 and 6 × ⅓ = 2. The corresponding point B' needs to be two squares to the right and two squares below the centre of enlargement.

Image caption, Draw a line to connect each new vertex. The enlargement of the shape is complete. Shape A'B'C' is an enlargement of a scale factor of ⅓, with point P as the centre of enlargement. The answer can be checked by drawing dashed lines through pairs of corresponding points. These lines all meet at the centre of enlargement, point P.
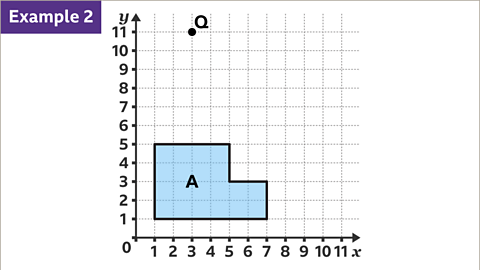
Image caption, It is possible to draw an enlargement by calculating the position of one vertex. The similar shape then needs to be drawn at the correct proportion using the scale factor. Shape A is to be enlarged by a scale factor of ½, with point Q as the centre of enlargement and positioned at the coordinates (3, 11).
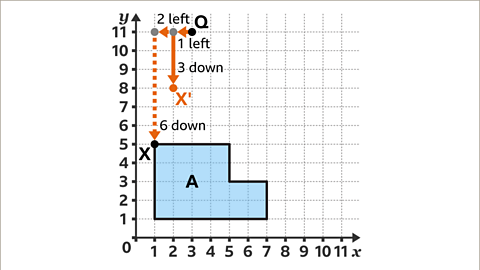
Image caption, Choose a vertex on the shape. In this example, Vertex X has been chosen with coordinate (1, 5). Vertex X is two squares to the left and six squares below the centre of enlargement. Multiply this displacement by the scale factor of a ½. 2 × ½ = 1 and 6 × ½ = 3. The corresponding point X' needs to be one square to the left and three squares below the centre of enlargement. X' has the coordinates (2, 8).
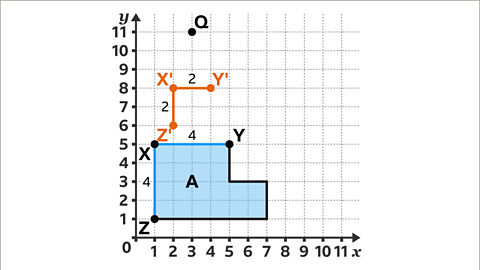
Image caption, Now that X' is in the correct position, a similar shape with edges half the size of B can be drawn. For example, using vertex Y with coordinate (5, 5), the length of XY is four squares long. In the enlargement, multiplying by a scale factor of ½, X'Y' will be two squares long. Similarly, using vertex Z with coordinate (1, 1), the length of XZ is four squares long. In the enlargement, multiplying by a scale factor of ½, X'Z' will be two squares long.
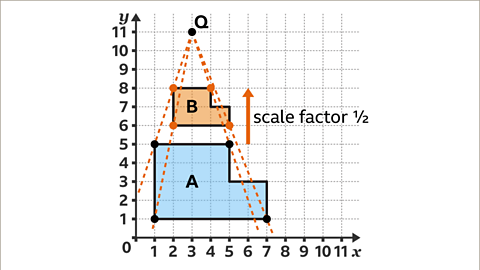
Image caption, Continue this process for the remaining edges. The shape is complete. Shape B is an enlargement of shape A by a scale factor of ½. The answer can be checked by drawing dashed lines through pairs of corresponding points. These lines meet at the centre of enlargement, point P.
1 of 9
Question
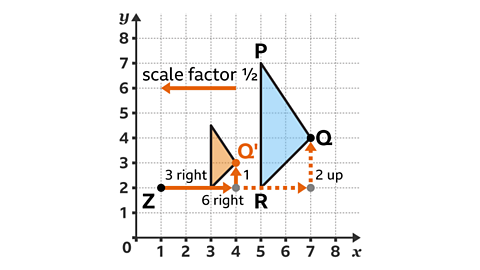
Triangle PQR is to be enlarged by a scale factor \( \frac{1}{2} \), with point Z as the centre of enlargement and with the coordinates (1, 2).
What is the new coordinate of vertex Q in the enlargement?
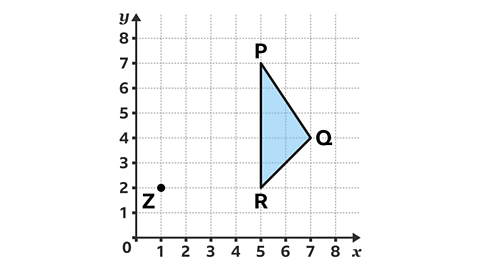
Vertex Q is six squares to the right and two squares above the centre of enlargement.
Multiply this displacement by the scale factor of a \( \frac{1}{2} \)6 × \( \frac{1}{2} \) = 3 and 2 × \( \frac{1}{2} \) = 1The corresponding point Q' needs to be three squares to the right and one square above the centre of enlargement.
Vertex Q' has the coordinates (4, 3).
Practise enlarging shapes
Quiz
Practise enlarging shapes with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths

A professional photographer can produce photos of different sizes. The most common photo size is approximately 4 inches by 6 inches. The length is 1.5 times longer than the width.
Photographs can be enlarged to produce bigger images, such as those that may be used in newspapers or magazines.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Symmetry and transformations
Find out more by working through a topic
- count1 of 6
- count2 of 6
- count3 of 6
- count4 of 6