Key points
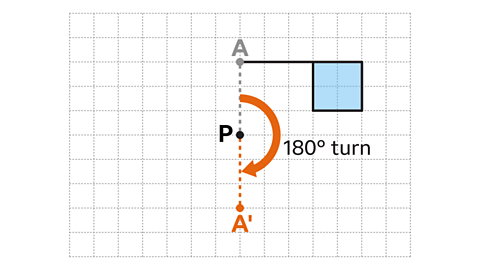
A rotationA turning effect applied to a point or shape. is one of the four types of transformationA change in position or size, transformations include translations, reflections, rotations and enlargements..
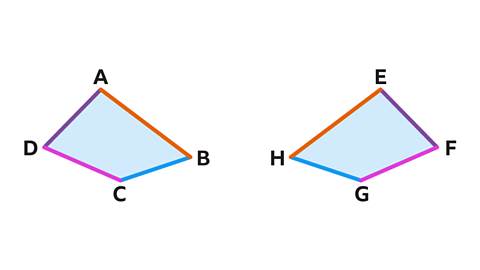
A rotation has a turning effect on a shape. The result is a congruentShapes that are the same shape and size, they are identical. shape.
Rotation turns a shape around a fixed point called the centre of rotationA fixed point about which a shape is rotated.. This point can be inside the shape, a vertexThe point at which two or more lines intersect (cross or overlap). The corner of a shape. The plural form is vertices. of the shape or outside the shape.
Rotations can be clockwiseTravelling in the same direction as the hands on a clock. or anti-clockwiseTravelling in the opposite direction to the hands on a clock. and a multiple of 90° (90°, 180° or 270°) is used.
To understand rotations, a good understanding of angles and rotational symmetry can be helpful.
To fully describe a rotation, it is necessary to specify the angle of rotation, the direction, and the point it has been rotated about.

Rotating about the centre of a shape
When rotationA turning effect applied to a point or shape. a shape about a central point the objectThe starting shape prior to a transformation. and the imageThe resultant position of a shape after a transformation. will always overlap.
A piece of tracing paper can be useful when plotting a rotation.
To work out the position of the new shape after a rotation:
- Place the tracing paper over the shape.
- Copy the shape on to the tracing paper.
- Rotate the tracing paper in the correct direction and the specified angle, keeping the centre of rotation fixed.
- The tracing paper now shows the position of the new shape.
- Remove the tracing paper and draw the shape in its new location.
Examples
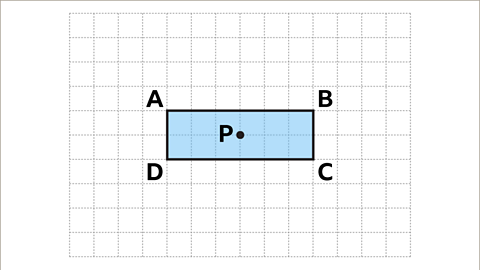
Image caption, Rectangle ABCD is to be rotated 90° clockwise about the centre of rotation, P.
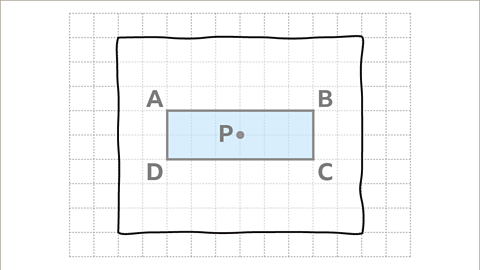
Image caption, Place the tracing paper over the shape and centre of rotation.
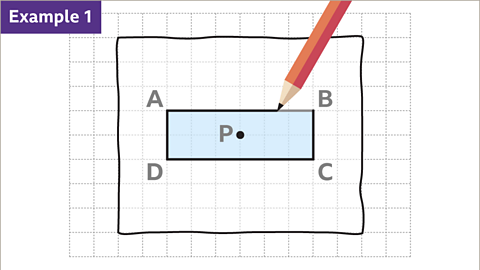
Image caption, Trace the shape with a pencil and mark the centre of rotation.
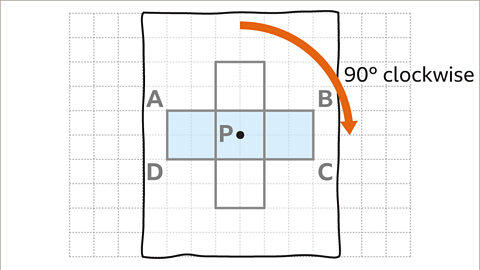
Image caption, Turn the tracing paper 90° clockwise keeping the centre of rotation fixed on the same point, P. This shows where the new shape’s location is.
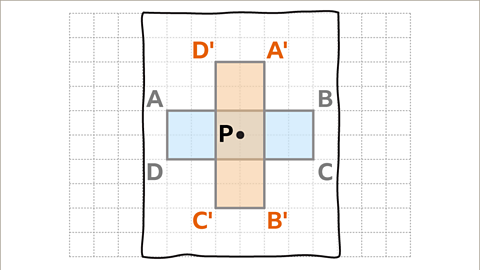
Image caption, Draw the shape in its new location. The new shape can be labelled with similar letters to explain where each vertex has been rotated to. Rectangle A'B'C'D' is a 90° clockwise rotation about point, P.
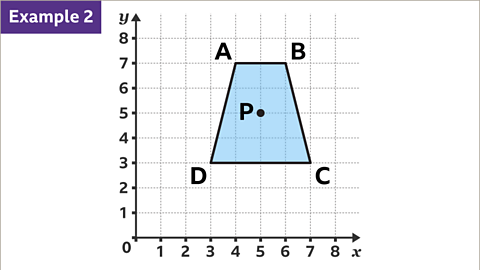
Image caption, Rotations can also occur on sets of axes. This problem can be approached in the same way. Trapezium ABCD is to be rotated 180° about the centre of rotation, P, with co-ordinate (5, 4).
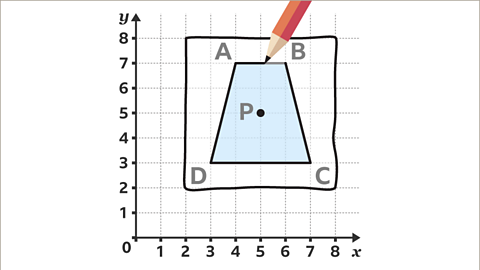
Image caption, Place the tracing paper over the shape and centre of rotation. Trace the shape with a pencil and mark the centre of rotation.
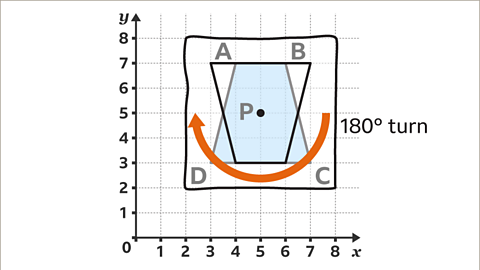
Image caption, Turn the tracing paper 180° keeping the centre of rotation on the same fixed point, P. For a rotation of 180° it does not matter if the turn is clockwise or anti-clockwise as the outcome is the same. This shows where the new shape’s location is.
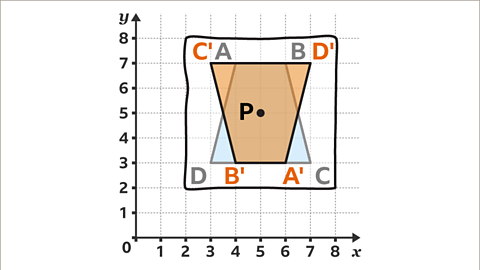
Image caption, Draw the shape in its new location. The new shape can be labelled with similar letters to explain where each vertex has been rotated to. Trapezium A'B'C'D' is a 180° rotation about point, P.
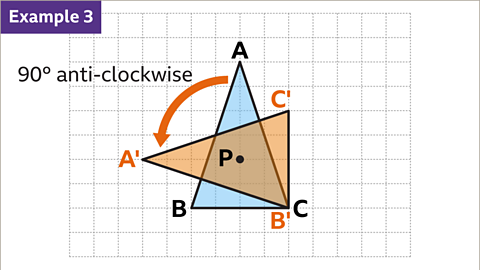
Image caption, To fully describe a rotation, it is necessary to specify the angle of rotation, the direction, and the point it has been rotated about. Triangle A'B'C' is a rotation 90° anti-clockwise (or 270° clockwise) about point P.
1 of 10
Question
The orange L-shape has been rotated about point P. What angle and direction has it been rotated by?
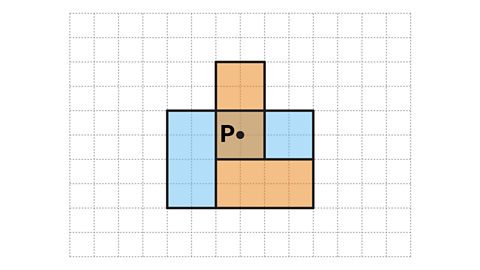
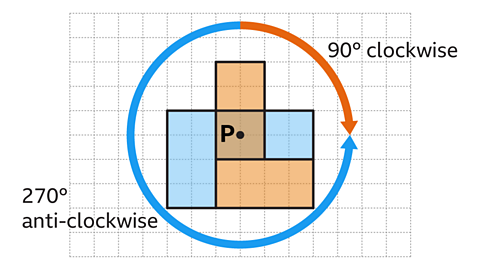
The L-shape has been rotated 90° clockwise (or 270° anti-clockwise) about P. This can be confirmed by using tracing paper, if required.
Rotating about other centre of rotations
The location of the centre of rotationA turning effect applied to a point or shape. affects the final position of the image. If the centre of rotation is a vertexThe point at which two or more lines intersect (cross or overlap). The corner of a shape. The plural form is vertices. of the object, then that point will remain unchanged invariantA vertex or line segment that does not change after a transformation. through the rotation.
It is possible to plot a rotation without tracing paper.
To work out the position of the new shape after a rotation:
- Imagine a line from the centre of rotation to a vertex on the shape.
- Rotate this line in the correct direction and the specified angle. keeping the centre of rotation fixed.
- The end of this line will correspondTwo vertices or line segments that match on similar or congruent shapes. to the new location of that vertex.
- Repeat the process for further vertices on the shape.
Examples
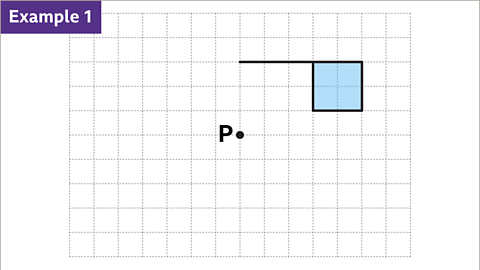
Image caption, Rotate the flag shape 180° about the centre of rotation, P.
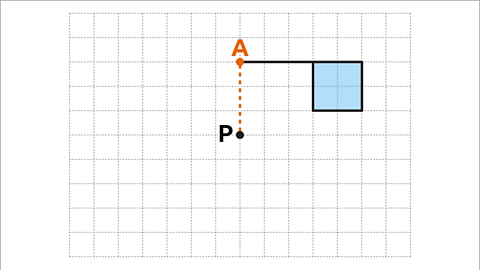
Image caption, Choose a vertex on the shape, for example A. Imagine a line from the centre of rotation, P, to the vertex marked A.
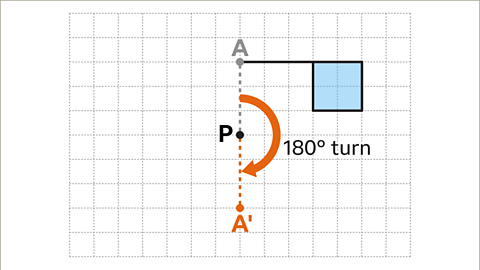
Image caption, Rotate the line segment AP 180°, keeping the centre of rotation P fixed. For a rotation of 180° it does not matter if the turn is clockwise or anti-clockwise as the outcome is the same. The end of this line, A', is the new position of point A.
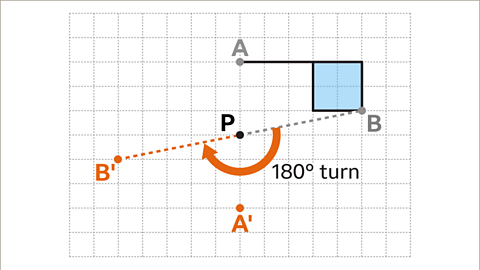
Image caption, Choose another vertex B and imagine a line from P to B. Rotate this line 180°. The end of this line is the new position of point B.
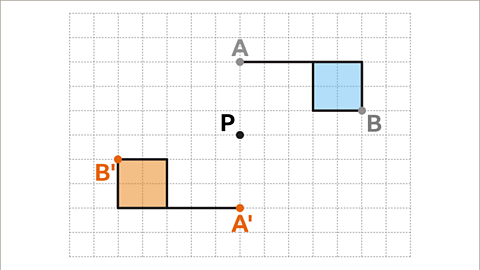
Image caption, Once this has been done for enough vertices it is possible to draw the whole image in its correct position. This can be checked by using tracing paper, if required.
Image caption, Triangle ABC is to be rotated 90° anti-clockwise about vertex C. Since vertex C is the centre of rotation it will remain unchanged.
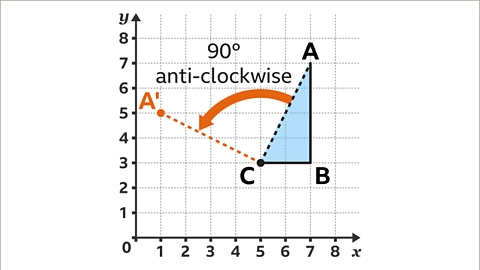
Image caption, Imagine a line segment AC rotated 90° anti-clockwise, keeping the centre of rotation C fixed. The end of this line is the new position of point A. A has rotated to (1, 5).
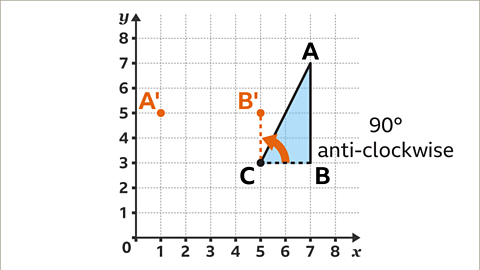
Image caption, Imagine line segment BC rotated 90° anti-clockwise, keeping the centre of rotation C fixed. The end of this line is the new position of point B. B has rotated to (5 , 5).

Image caption, With all three vertices now plotted the rotated shape can be completed. The image is a rotation, 90° anti-clockwise about vertex C.
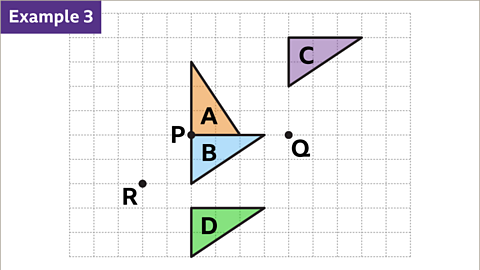
Image caption, The location of the centre of rotation affects the final position of the shape. Each of these triangles is a rotation of triangle A, 90° clockwise. B is a rotation 90° clockwise about point P. C is a rotation 90° clockwise about point Q. D is a rotation 90° clockwise about point R. Notice the orientation of each solution is the same but the position is different.
1 of 10
Question
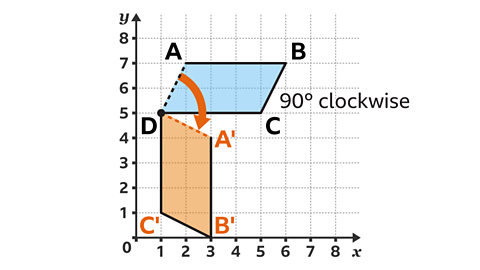
The parallelogramA four-sided shape with two pairs of parallel sides. The opposites sides and angles are equal. ABCD is rotated 90 clockwise about point D. Which coordinate is point A rotated to?
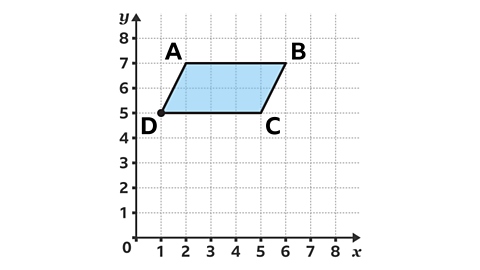
Imagine line segment AD rotated 90° clockwise, keeping the centre of rotation D fixed. The end of this line is the new position of point A. A has rotated to (3, 4).
Practise rotation and rotating a shape about a given point
Quiz
Practise rotation and how to rotate a shape about a given point in this quiz. You may need a pen, paper and tracing paper for this quiz.
Real-life maths

A gymnast is required to perform complicated tumbling when competing on a variety of apparatus or as a floor exercise. Many of these routines involve acrobatics where the competitor is rotating.
For example, on the pommel horse a gymnast can perform a move called circles. Circles requires the competitor to rotate or swing their legs around the apparatus whilst alternating their hand positions on the pommels (handles). Some events require an elaborate dismount. This could include a somersault where a person’s body rotates 360°.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Symmetry and transformations
Find out more by working through a topic
- count5 of 6
- count6 of 6
- count1 of 6
- count2 of 6