Key points
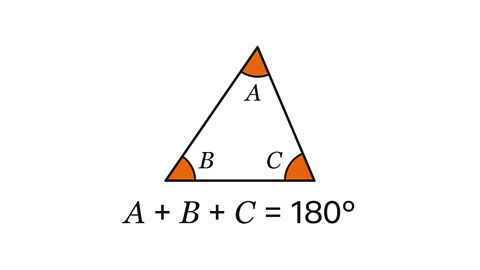
All polygonA 2D shape with straight sides that are fully closed. have interior angles. The number of angles is equal to the number of sides it has.
triangleA polygon with three straight sides. have three sides, therefore they have three angles. Interior angles in a triangle sum to a half turn (180˚).
Interior angles in an equilateral triangleA triangle with all three sides of equal lengths. All the angles are 60°. are equal. Base interior angles in an isosceles triangleA triangle with two equal sides. This means two angles are equal. are equal.
quadrilateralA polygon with four straight sides. have four sides and four angles. Interior angles in a quadrilateral sum to a full turn (360˚).
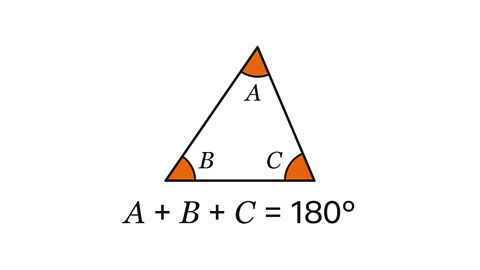
Video
Watch the video to learn how it is possible to prove mathematically that the angle sum of every triangle is 180°.
It's possible to demonstrate and prove mathematically that the angle sum of every triangle is 180 degrees. The techniques used are useful for solving all kinds of other geometry problems too.
There are two rules to remember. First, when a diagonal line is drawn crossing two parallel lines, it forms alternate angles that are equal. That's these two.
Second, angles on a straight line add up to 180 degrees. Using these two rules it's possible to prove that angles in a triangle add up to 180
Back to the bridge. To start, draw two parallel lines. One that follows an edge of the triangle and one through the vertex opposite that edge. Now both rules are in play - the alternate angles rule and the rule the angles in a straight line add up to 180
If angle 𝑎 equals angle 𝑥 and angle 𝑦 equals angle 𝑏, our first rule. And if angles 𝑥, 𝑦 and 𝑐 equal 180, our second rule. Then angles 𝑎, 𝑏 and 𝑐 must equal 180 as well.
This proves that the angles of a triangle must add up to 180 degrees.
Angles in a complete turn and angles in triangles
A complete turn is a 360˚ rotation.
To find unknown angles in a complete turn:
Add the known angles.
Form an equation equal to 360˚.
Subtract the sum of the known angles from the sum of a complete turn (360˚).
Triangles have three interior angles. They are formed at the vertices (corners).
The sum of these angles is 180˚.
In scalene triangleA triangle where all three sides are different lengths. All the angles are different. , each angle is a different size because each side is a different length.
To find the missing angles in a triangle:
Add the known angles.
Subtract the sum of the known angles from the sum of interior angles in a triangle (180˚).
Example
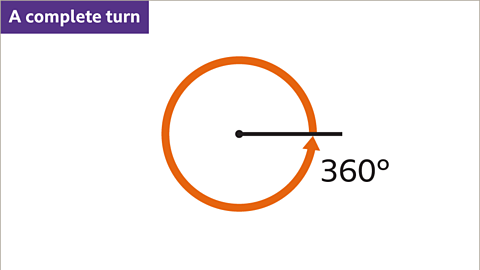
Image caption, A complete turn is 360˚.
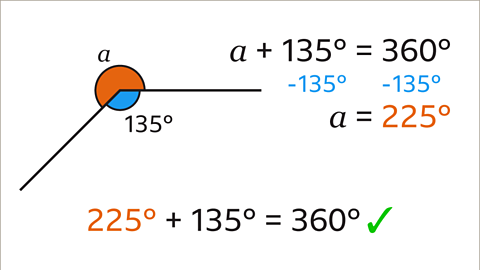
Image caption, There is one missing angle in this complete turn. To find the size of the missing angle, first form an equation that is equal to 360˚. 𝒂 + 135 = 360. Then make 𝒂 the subject of the equation with 𝒂 = 360 − 135. This means that the unknown angle (𝒂) is 225˚. This can be checked by adding the two angles together to make sure they create a full turn (360˚). 225 + 135 = 360
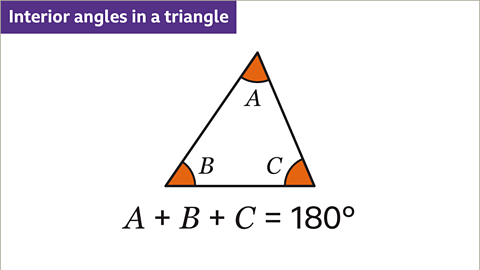
Image caption, The sum of the three interior angles in a triangle is 180˚.
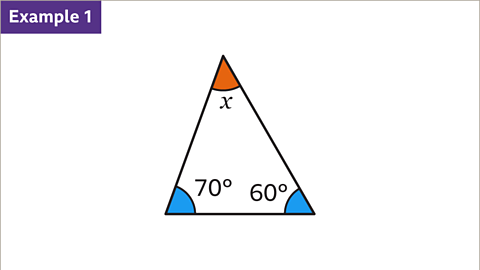
Image caption, There are three angles in this triangle. They must add up to 180˚. Two angles are given but one is unknown (𝒙).
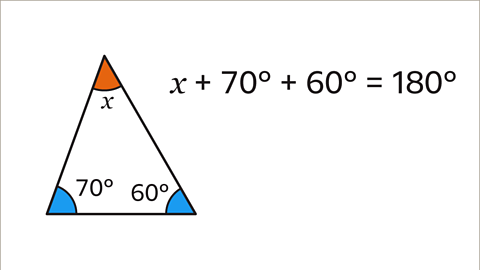
Image caption, Form an equation that is equal to 180˚. 𝒙 + 70 + 60 = 180.
Image caption, Work out the value of the angle 𝒙 by solving the equation.
Image caption, The value of angle 𝒙 is 50˚.
Image caption, To check that the value of 𝒙 is correct, add the three angles together. They should sum to 180˚. 70 + 60 + 50 = 180
1 of 8
Question
Find the size of the missing angle, \(a\).
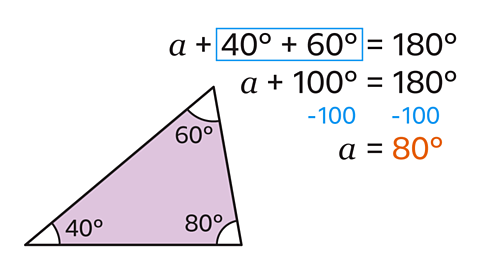
Angles in a triangle add up to 180˚.
First form an equation that is equal to 180˚. The equation that can be formed is \(a\) + 40 + 60 = 180
Then, we can solve the equation:
\(a\) + 100 = 180
\(a\) = 180 - 100
\(a\) = 80
The size of the missing angle, \(a\), is 80˚.
To check that the value of \(a\) is correct, add the three angles together.
40 + 60 + 80 = 180˚.
Interior angles of equilateral and isosceles triangles
The sum of interior angles in a triangle is 180˚.
In an equilateral triangle, all three angles are equal to 60˚.
To find the missing angles in an equilateral triangle, divide the sum of interior angles in a triangle by 3
In an isosceles triangle, two of the sides are equal.
This means two of the angles are equal. These are the base angles.
The base angles are opposite the equal sides.
Examples
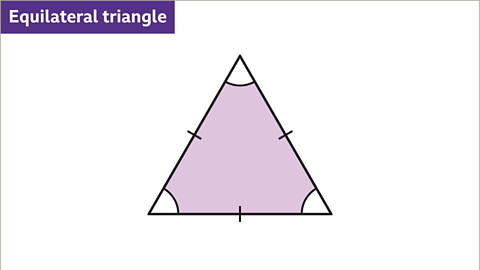
Image caption, An equilateral triangle has three equal sides. This is shown by the hatch marks on each side. This means that the three angles will also be equal.
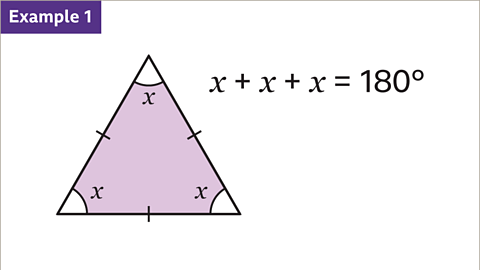
Image caption, There are three equal angles in this triangle because there are three equal sides. All three angles must add up to 180˚. Label the angles with a variable and form an equation that is equal to 180˚.
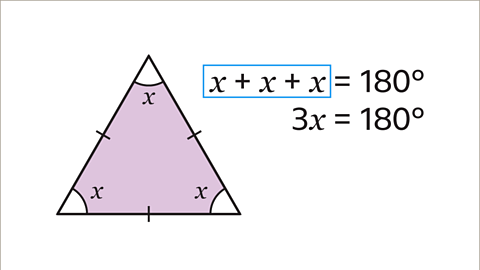
Image caption, Work out the value of the angle 𝒙 by solving the equation, 𝒙 + 𝒙 + 𝒙 = 180˚. 3𝒙 = 180˚.
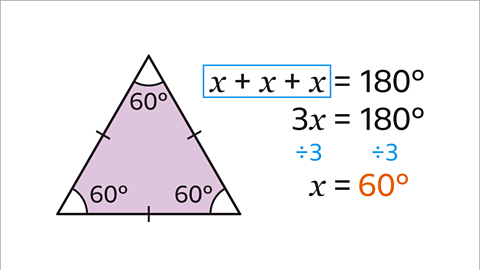
Image caption, The value of angle 𝒙 is 60˚, 180 ÷ 3 = 60
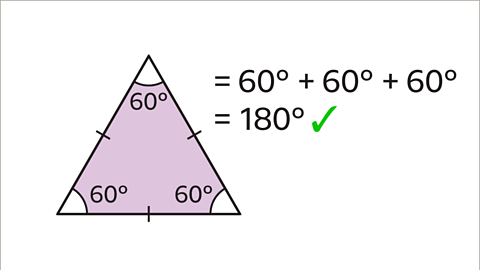
Image caption, To check that the value of 𝒙 is correct, add the three angles together. They should sum to 180˚.
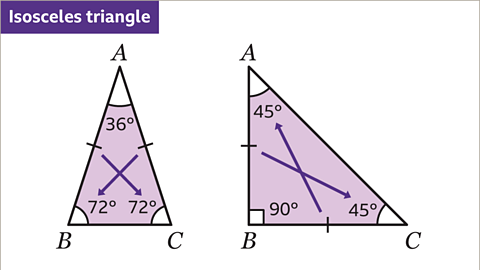
Image caption, An isosceles triangle has two equal sides. These are shown by the hatch marks. This means that the two base angles (opposite the equal sides) will also be equal.
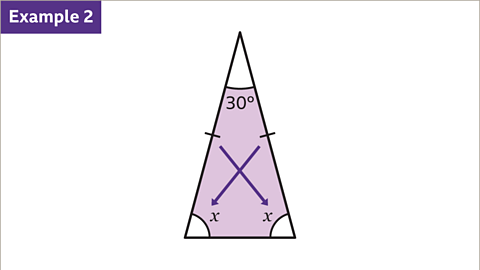
Image caption, This is an isosceles triangle. Two of the angles are equal because there are two equal sides. All three angles must add up to 180˚.
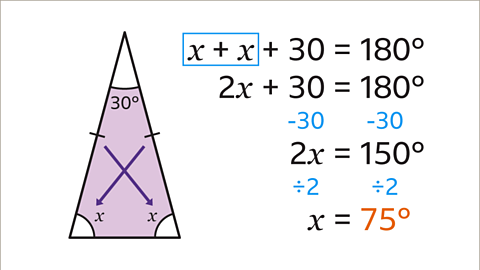
Image caption, Form an equation by making 𝒙 + 𝒙 + 30 = 180. Work out the value of the angle 𝒙 by solving the equation, 𝒙 + 𝒙 + 30 = 180˚. Therefore 2𝒙 + 30 = 180. This means that 2𝒙 = 150. The value of angle 𝒙 = 75˚, 150 ÷ 2 = 75
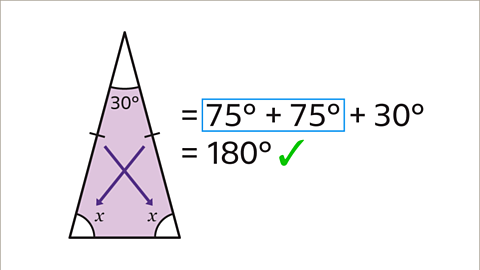
Image caption, To check that the value of 𝒙 is correct, add the three angles together. They should sum to 180˚.
1 of 9
Question
Find the size of the missing angle, \(x\).
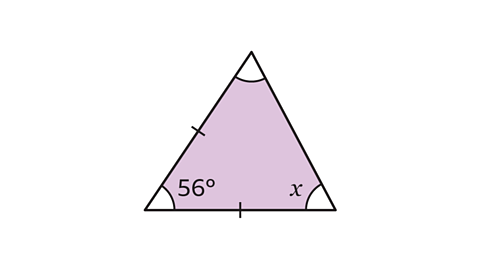
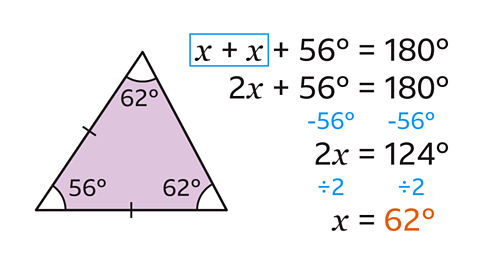
As two of the sides are equal, the base angles are equal sizes.
The equation that can be formed to find the value of the base angles is:
\(x\) + \(x\) + 56 = 180
The equation can then be solved:
2\(x\) + 56 = 180
2\(x\) = 180 – 56
2\(x\) = 124
\(x\) = 124 ÷ 2
\(x\) = 62
The size of the missing angle, \(x\), is 62˚.
To check that the value of \(x\) is correct, add the three angles together.
56 + 62 + 62 = 180˚.
Interior angles in quadrilaterals
The sum of interior angles in a quadrilateral is 360˚.
In a square or rectangle, each interior angle is 90˚.
In irregular quadrilaterals, each angle is a different size.
To find a missing angle in an irregular quadrilateral:
Add the known angles.
Subtract the sum of the known angles from the sum of interior angles in a quadrilateral (360˚).
Examples
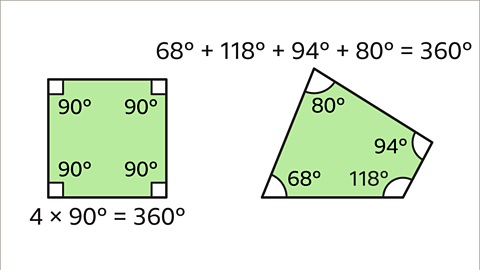
Image caption, A quadrilateral has 4 angles. If the quadrilateral is irregular, all the angles are different.
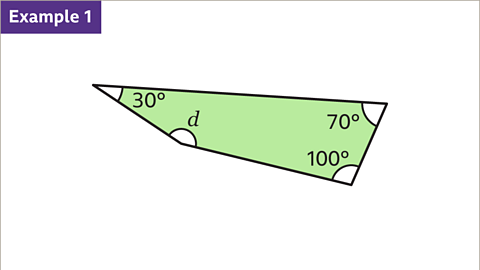
Image caption, An irregular quadrilateral has four different sides. This means all of the angles are different sizes. All four angles add up to 360˚.
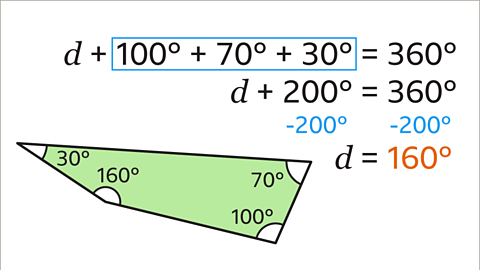
Image caption, Form an equation by making 𝒅 + 100 + 70 + 30 = 360. Work out the value of the angle 𝒅 by solving the equation 𝒅 + 200 = 360, 360 – 200 = 160. This means that the value of 𝒅 = 160˚. The missing angle is 160˚.
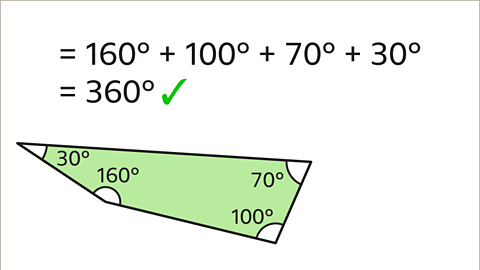
Image caption, To check that the value of 𝒅 is correct, add the four angles together. They should sum to 360˚.
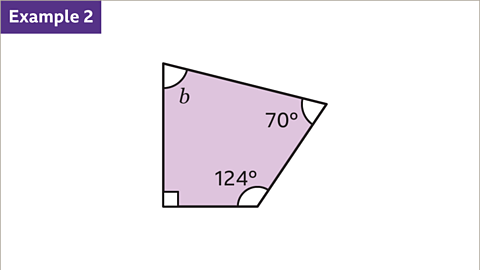
Image caption, Find the size of angle 𝒃.
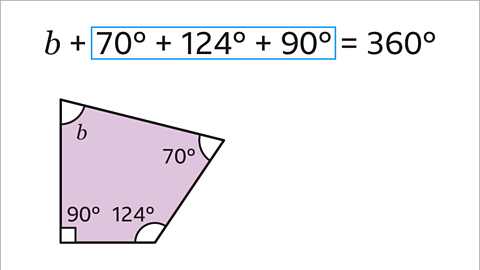
Image caption, In this quadrilateral, it looks like there are two missing angles. However, the angle represented by a box is a 90˚ right angle. Form an equation by making 𝒃 + 70 + 124 + 90 = 360
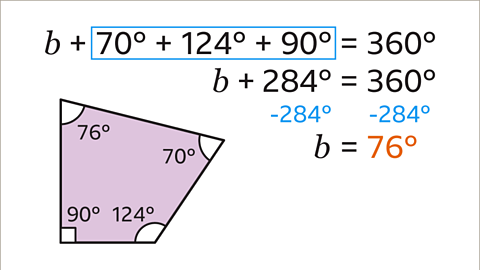
Image caption, Work out the value of the angle 𝒃 by solving the equation, 𝒃 + 70 + 124 + 90 = 360. This means that 𝒃 + 284 = 360. 𝒃 = 360 – 284. 𝒃 = 76˚. The missing angle is 76˚.
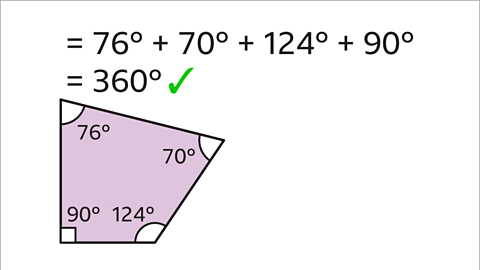
Image caption, To check that the value of 𝒃 is correct, add the four angles together. They should sum to 360˚.
1 of 8
Question
Find the size of the missing angle, \(x\).
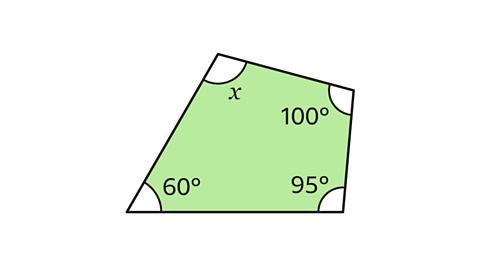
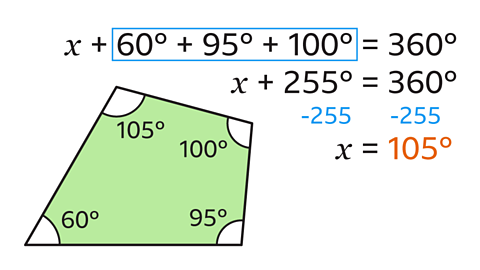
The equation that can be formed to find the value of \(x\) is:\(x\) + 60 + 95 + 100 = 360˚.
The equation can then be solved:
\(x\) + 255 = 360
\(x\) = 360 – 255
\(x\) = 105
The size of the missing angle, \(x\), is 105˚.
To check that the value of \(x\) is correct, add the four angles together.
105 + 60 + 95 + 100 = 360
Practise finding angles in triangles and quadrilaterals
Quiz
Practise finding angles in triangles and quadrilaterals with this quiz. You may need a pen and paper to help you with your answers.
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Angles
Find out more by working through a topic
- count3 of 7
- count4 of 7
- count5 of 7

- count6 of 7