KS3

Constructing triangles

Part ofMathsAngles

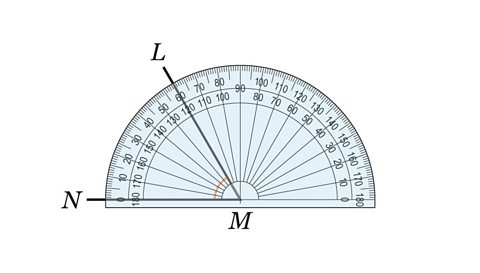
Key points

A ruler, a and a are required to a triangle accurately.

An image of construction tools; a ruler, a protractor, a pair of compasses and a pencil. — Image caption,
A ruler, protractor and compass are used in constructing triangles.

A triangle has three sides and three angles. To construct a triangle, one of three properties must also be known:
- Two sides and the angle between them (SAS)
- Two angles and the side between them (ASA)
- Three sides (SSS)
After the triangle has been constructed, it is important to leave the . This is to show each stage of the process clearly.

An image of construction tools; a ruler, a protractor, a pair of compasses and a pencil. — Image caption,
A ruler, protractor and compass are used in constructing triangles.

Using a protractor to construct a triangle

There are two ways to construct a triangle using a ruler and a protractor.

The first is a Side, Angle, Side (SAS) construction where two sides and the angle between them is known.
The second is an Angle, Side, Angle (ASA) construction where two angles and the side between them is known.
To construct an SAS triangle:
1. Draw the longest given side of the triangle using a ruler.
2. Use a protractor to measure the given angle from the left-hand of the longest given side, mark it with a cross and draw a line from the endpoint through this cross.
3. Using a ruler, measure along the line drawn from the left hand endpoint to the cross and mark the length of the other given side on it.
4. Join the longest given side and the other given side together to produce a triangle.
5. Label the sides and the angle, leaving the construction lines.
To construct an ASA triangle:
1. Draw the given side of the triangle using a ruler.
2. Use a protractor to measure the angle from the left-hand endpoint of the given side, mark it with a cross and draw a line from the endpoint through this mark.
3. Use a protractor to measure the angle on the right-hand endpoint of the given side, mark it with a cross and draw a line from the endpoint through this mark.
4. Label the angles and side, leaving the construction lines.

Examples

Skip image gallery

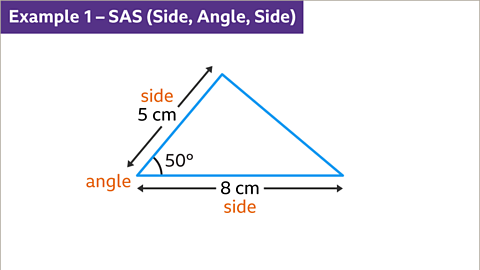
Image caption,
In this triangle two sides, 5 cm and 8 cm, and the angle between them, 50⁰, are known. This is an SAS (Side, Angle, Side) construction, which can be constructed using a protractor and a ruler.
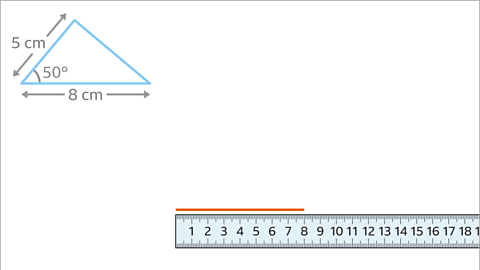
Image caption,
Draw the longest given side (8 cm) using a ruler.
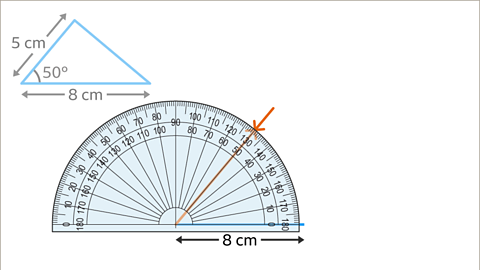
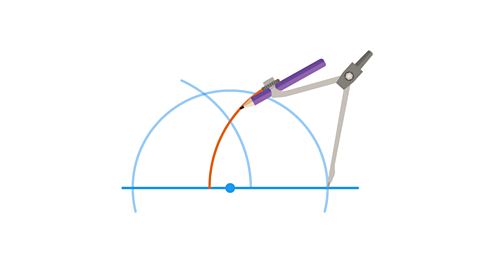
Image caption,
Using a protractor, measure an angle of 50⁰ on the left-hand endpoint of the longest given side, mark it with a cross and draw a line.
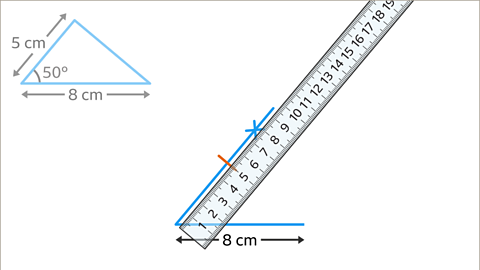
Image caption,
Measure 5 cm along this line using a ruler and mark it.
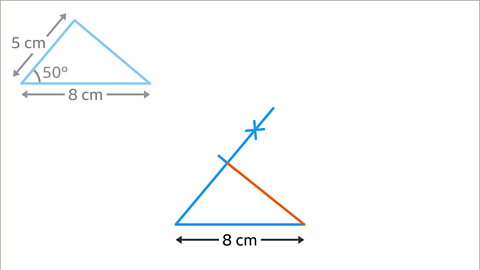
Image caption,
Using a ruler, join the 5 cm marked point along the line to the other endpoint of the 8 cm line. Label the sides of the shape with the correct measurements. Make sure to leave the construction lines in to make it clear that the triangle has been accurately drawn.
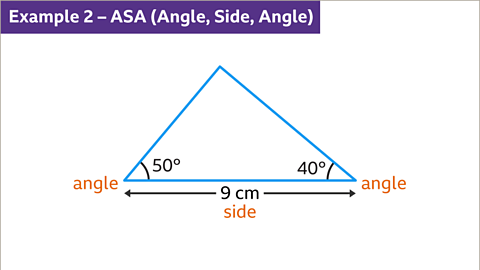
Image caption,
In this triangle two angles, 50⁰ and 40⁰, and the side between them, 9 cm, are known. This is an ASA (Angle, Side, Angle) construction, which can be constructed using a protractor and a ruler.
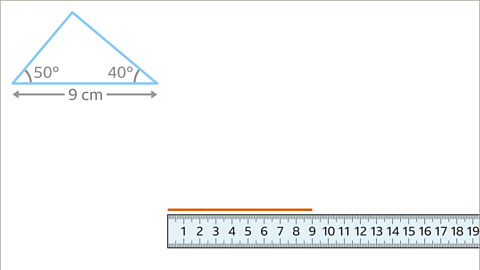
Image caption,
Draw the side of 9 cm using a ruler.
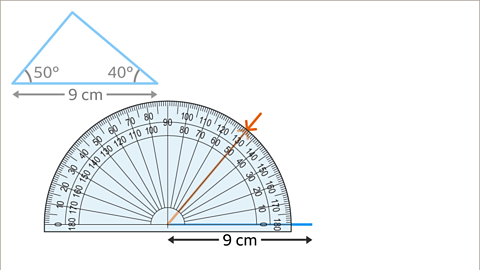
Image caption,
Using a protractor, measure an angle of 50⁰ on the left-hand endpoint of the 9 cm line (to match the original triangle), mark it with a cross and draw a line.
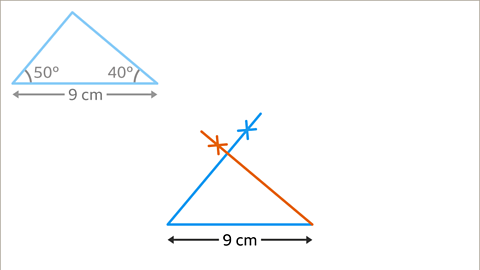
Image caption,
Using a protractor, measure an angle of 40⁰ on the right-hand endpoint of the 9 cm line (to match the original triangle), mark it with a cross and draw a line.
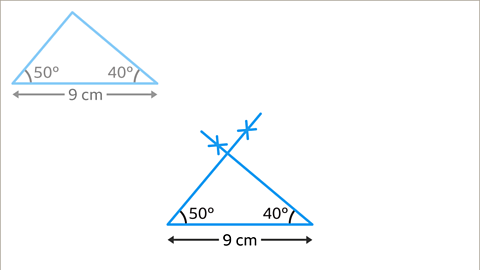
Image caption,
Label the sides of the shape with the correct measurements. Make sure to leave the construction lines in to make it clear that the triangle has been accurately drawn.

Question

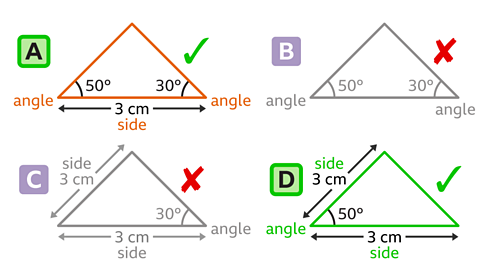
Which triangles can be constructed using a protractor and a ruler?

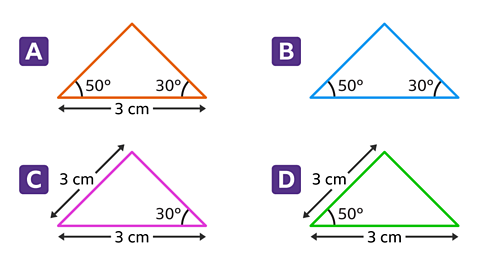
A series of four images. Image A is a triangle. The triangle has two angles and the included side labelled. The base of the triangle is labelled; three centimetres. The angle to the left of the base is labelled; fifty degrees. The angle to the right of the base is labelled; thirty degrees. The triangle’s outline is coloured orange. Image B is a triangle. The triangle has two angles labelled. The angle to the left of the base is labelled; fifty degrees. The angle to the right of the base is labelled; thirty degrees. The triangle’s outline is coloured blue. Image C is a triangle. The triangle has two sides and an angle labelled. The base of the triangle is labelled; three centimetres. The angle to the right of the base is labelled; thirty degrees. The side to the left of the base is labelled; three centimetres. The triangle’s outline is coloured purple. Image D is a triangle. The triangle has two sides and the included angle labelled. The base of the triangle is labelled; three centimetres. The length of the side on the left is labelled; three centimetres. The length of the included angle, between the two sides is labelled; fifty degrees.

Constructing a triangle using a compass

There is one way to a triangle using a ruler and a .

If all three sides are known, it can be constructed using a compass and a ruler. This is called an SSS (Side, Side, Side) construction.
To construct an SSS triangle:
1. Draw the longest side of the triangle using a ruler.
2. Use a compass to draw an from each of the line, measuring the length of the other two sides.
3. Draw a line from the endpoint of each side of the base to the point where the arcs meet.
4. Label the angles and side, leaving the .

Example

Skip image gallery

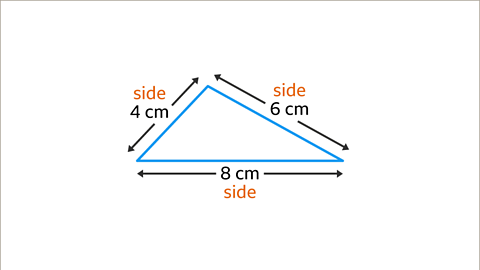
Image caption,
In this triangle all three sides are known, 4 cm, 6 cm and 8cm. This is an SSS (Side, Side, Side) construction, and the triangle can be constructed using a compass and a ruler.
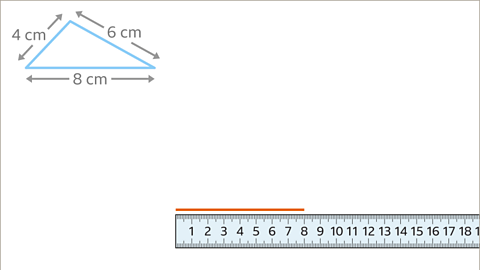
Image caption,
Draw the longest side (8 cm) using a ruler.
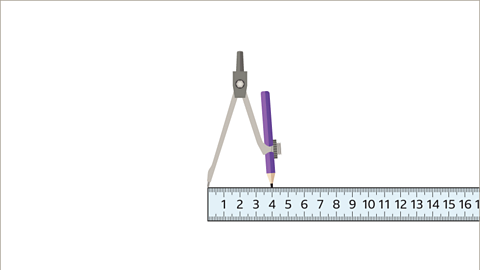
Image caption,
Set the compasses to 4 cm apart.
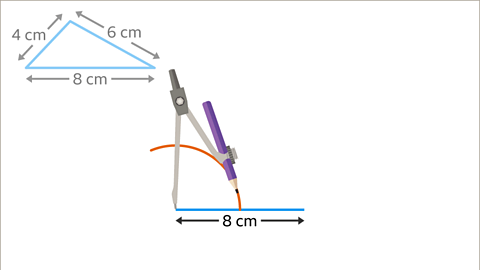
Image caption,
Draw an arc of 4 cm on the left-hand endpoint of the 8 cm line (to match the original triangle).
Image caption,
Now set the compasses to 6 cm apart.
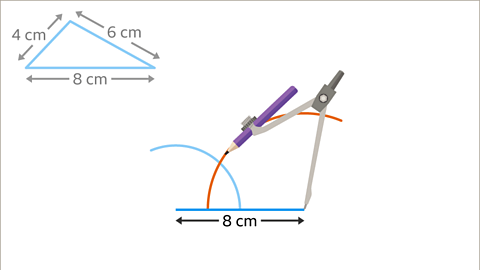
Image caption,
Draw an arc of 6 cm on the right-hand endpoint of the 8 cm line (to match the original triangle).
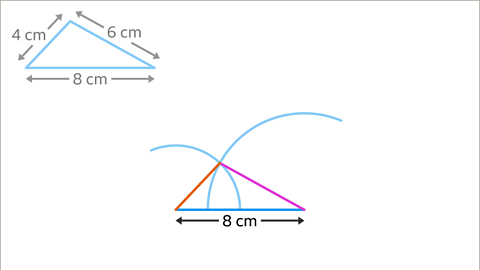
Image caption,
Join each endpoint to the point where both arcs meet.
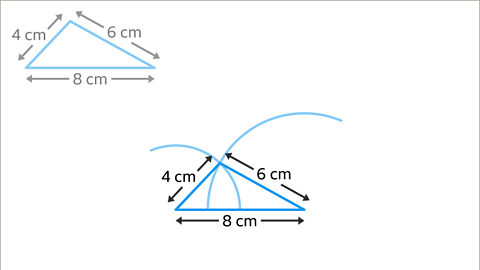
Image caption,
Label the sides of the shape with the correct measurements. Make sure to leave the construction lines in to make it clear that the triangle has been accurately drawn.

Question

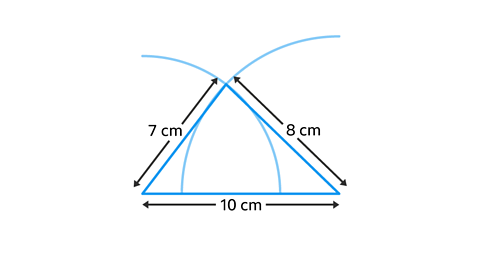
What equipment is needed to construct a triangle of 7 cm, 8 cm and 10 cm?

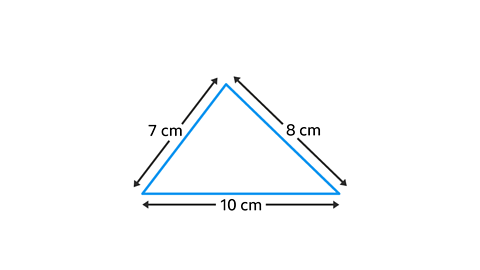
An image of a triangle. The triangle has three sides labelled. The base of the triangle is labelled; ten centimetres. The length of the side on the left is labelled; seven centimetres. The length of the side on the right is labelled; eight centimetres. The triangle’s outline is coloured blue.

Practise working out how to construct triangles

Practise working out how to construct triangles with this quiz. You will need a pencil, compass, protractor, ruler and paper to help you with some of your answers.

Quiz

Real-life maths

An image of an architect using construction tools to create a plan. — Image caption,
Architects use mathematical equipment to ensure precise designs.

Being able to use mathematical equipment and techniques correctly to construct lines and angles in shapes is essential to the work of an architect.

When an architect produces construction designs for new homes and buildings, it is important that these designs are accurate and clear. Architects need to use the right equipment to ensure their designs are precise before the plans are moved onto the next stage of the process.

An image of an architect using construction tools to create a plan. — Image caption,
Architects use mathematical equipment to ensure precise designs.

More on Angles

Find out more by working through a topic

Angles in polygons
count
5 of 7
Polygons - sum of interior angles
count
6 of 7
Bisecting lines and angles
count
7 of 7
Drawing and measuring angles
count
1 of 7