Bisecting lines and angles - KS3 Maths

Key points

An image of a ruler and pair of compasses, with pencil. — Image caption,
Constructions (accurate drawings) can be made using a ruler, a pair of compasses and a pencil.

A line which cuts another line into two equal parts and meets it at a right angle is called a bisector.
A line which cuts an angle into two equal side angles is called an angle bisector.
In geometry a construction is an accurate drawing. There are two main constructions which can be done using a ruler, a pair of compasses and a pencil.
After the construction is finished, it is important to leave the . This is to show each stage of the process clearly.

How to construct a perpendicular bisector

A bisector is a line which cuts another line exactly in half.

A perpendicular bisector cuts a line exactly in half and it at a right angle. It can be constructed using a ruler and pair of compasses.

To construct a perpendicular bisector:

Using a ruler, draw a straight line.
Place the compasses on the left-hand of the line and set them to just over half way along the line. Draw an .
Without changing the position of the compasses, repeat this with the right-hand endpoint of the line.
Draw a line between each point of intersection of the arcs. The of the perpendicular bisector and the original line is exactly halfway along the line.

Example

Skip image gallery

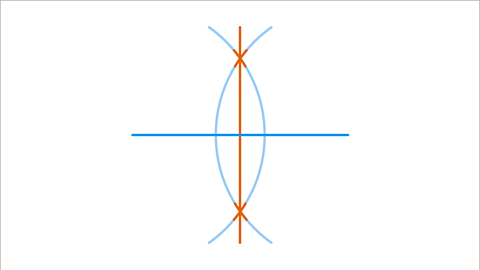
Image caption,
How to construct a perpendicular bisector.
Image caption,
To construct a perpendicular bisector, begin by drawing a straight line.
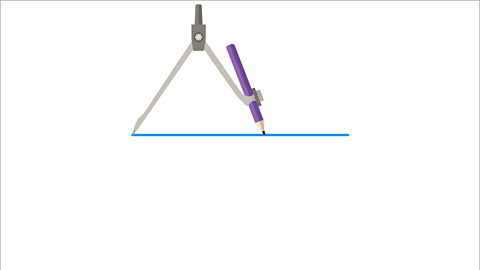
Image caption,
Place the compasses on the left-hand endpoint of the line and position the pencil to just over halfway along the line. Make sure the pair of compasses is not loose and the pencil is firmly in place so the distance between the point and the pencil does not change.
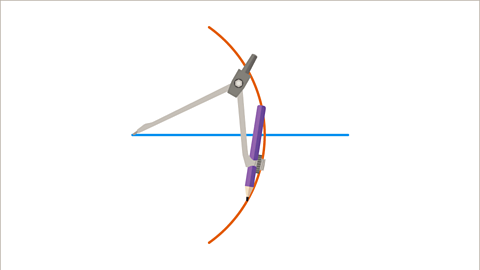
Image caption,
Draw an arc above and below the line.
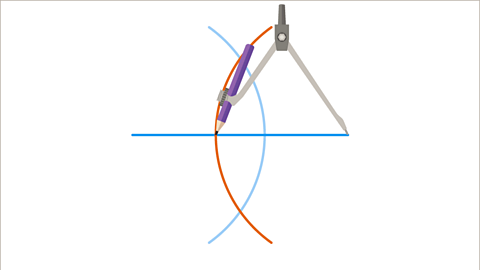
Image caption,
Draw another arc from the right-hand endpoint.
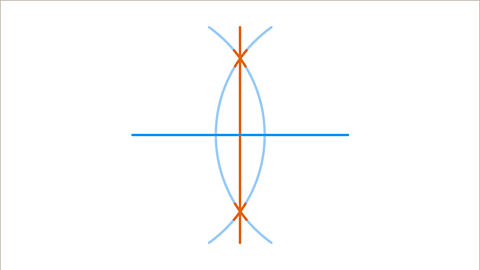
Image caption,
Draw a line between the two points of intersection of the arcs.
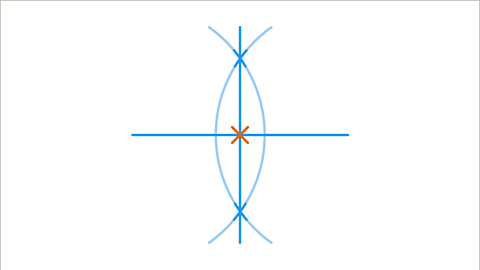
Image caption,
This line is the perpendicular bisector. The point of intersection of the perpendicular bisector and the original line is exactly halfway along the first line. If everything has been constructed correctly, the two lines will always meet at a right angle.

Question

When constructing a perpendicular bisector, how many arcs must be drawn?

An image of a vertical and horizontal line intersecting at a central point. The lines are coloured blue.

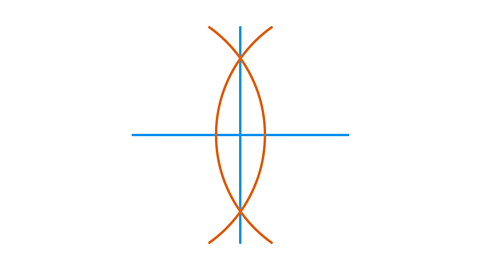
How to construct a perpendicular from a point to a line

To construct a from a point to a line:

Place the compasses on the point and set them to just below the line. Draw an which crosses the line twice.
Place the compasses on the left-hand between the arc and the line, then draw another arc below the line.
Without changing the compasses, do the same on the right-hand side.
Draw a line between the point of intersection of the new arcs and the point.

To construct a perpendicular through a point on a line:

Place the compasses on the point and draw an arc which crosses the line once on either side of the point.
Place the compasses on the left-hand point of intersection, set them to just over halfway along the line, and draw another arc which intersects the first arc.
Without changing the compasses, do the same on the right-hand side.
Draw a line between the point of intersection of the two new arcs and the point.Even the smallest inaccuracy at any point will create an error in the final angle. A sharp pencil is important to ensure accuracy.

Examples

Skip image gallery

Image caption,
To construct a perpendicular from a point to a line, draw a line and add a point above it for the perpendicular to intersect.
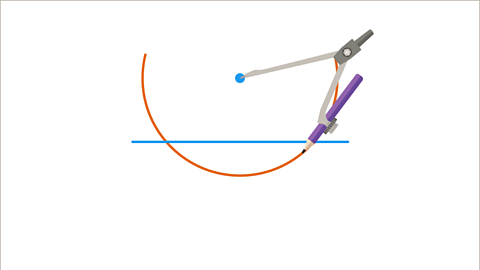
Image caption,
Place the compasses on the point, extend the pencil to just meet the line and draw an arc, just below the line.
Image caption,
Draw another arc from the left-hand endpoint below the line.
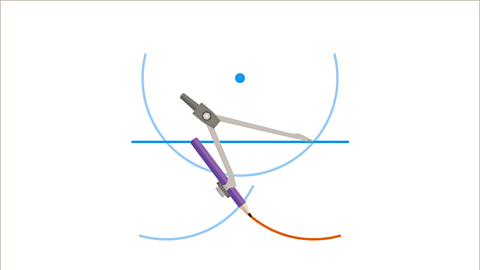
Image caption,
Without changing the compasses, repeat this from the right-hand endpoint: i.e the action as shown in slides 3 and 4 needs to be repeated on the right-hand side.
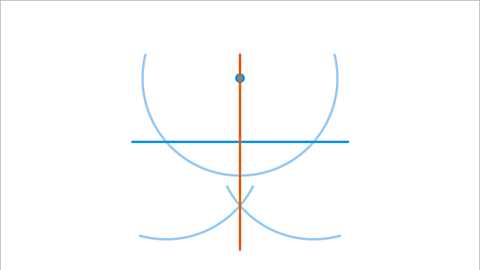
Image caption,
The two new arcs will intersect once. Draw a line from the point to this intersection. If drawn accurately, with a pair of compasses and ruler, this line will be perpendicular to the original line.
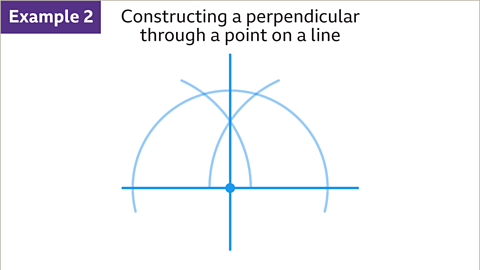
Image caption,
How to construct a perpendicular through a point on a line.
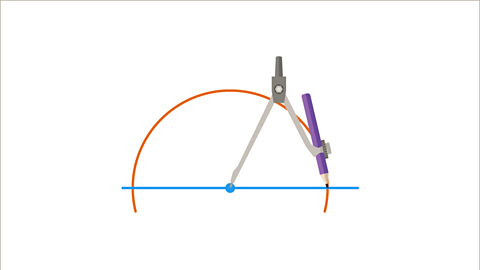
Image caption,
Place the compasses on the point and draw an arc which crosses the line once on either side of the point.
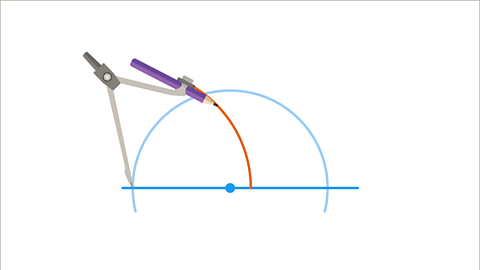
Image caption,
Place the compasses on the left-hand intersection and set the pencil to be just past the point. Draw a smaller arc.
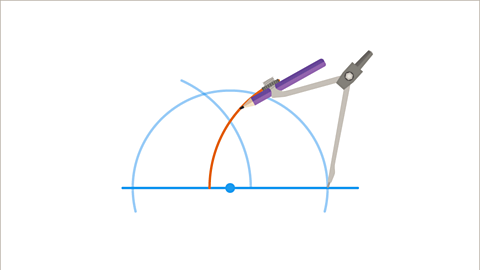
Image caption,
Repeat on the right-hand point of intersection without adjusting the compasses.
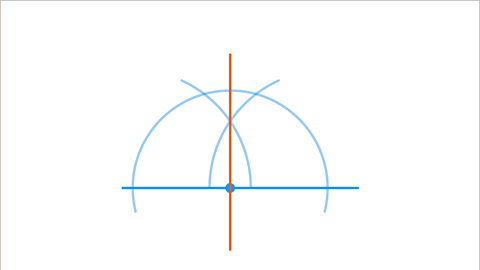
Image caption,
The two new arcs will intersect once. Draw a line from the point to this intersection. If drawn accurately, using a pair of compasses and a ruler, this line will be perpendicular to the original line and go through the given point.

How to construct an angle bisector

A bisector is a line which cuts another line exactly in half.

An angle bisector cuts an angle into two angles of equal size. It can be constructed using a ruler and a pair of compasses.

To construct an angle bisector:

Using a ruler, draw two lines which meet at a point. This makes an angle.
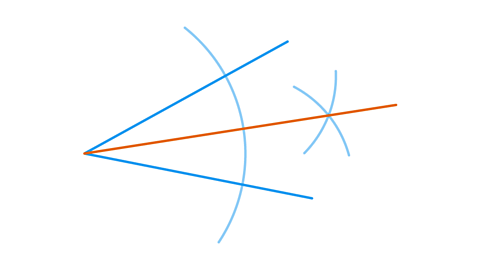
Place the compasses at the point where the two lines meet and draw an which crosses both lines.
At each of the lines and the arc, draw smaller arcs.
Draw a line between the point of intersection of the new arcs and the point where both lines meet.

This method, combined with constructing a bisector, can be used to accurately construct a 45° angle.

Examples

Skip image gallery

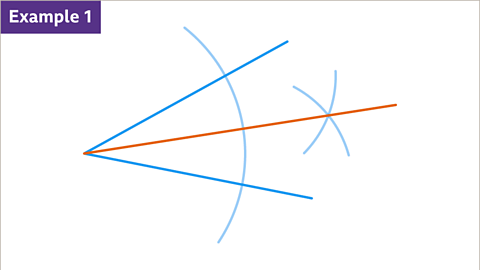
Image caption,
How to construct an angle bisector.
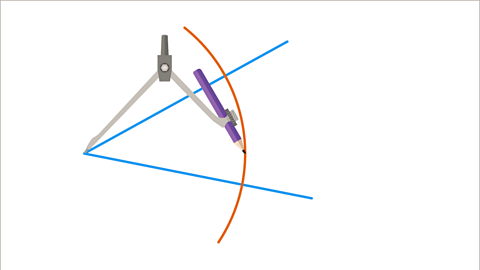
Image caption,
To bisect this angle, place the compasses on the point where both lines intersect and draw an arc.
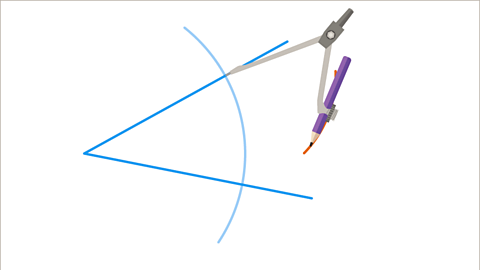
Image caption,
Place the compasses on one point of intersection between the line and arc, then draw a smaller arc.
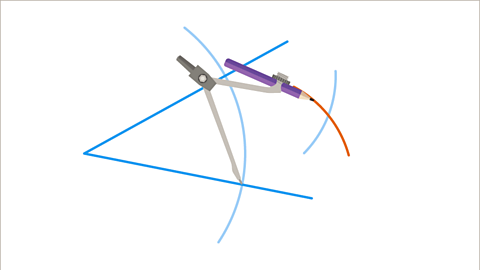
Image caption,
Without adjusting the compasses, repeat at the other point of intersection.
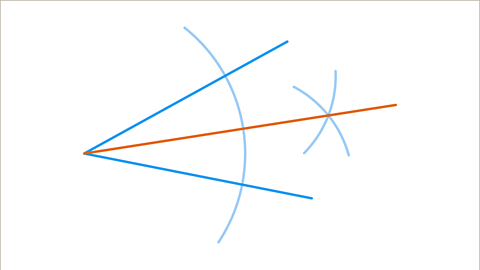
Image caption,
The two new arcs will intersect once. Draw a line from the first point to this intersection. If drawn accurately, this line will bisect the angle.
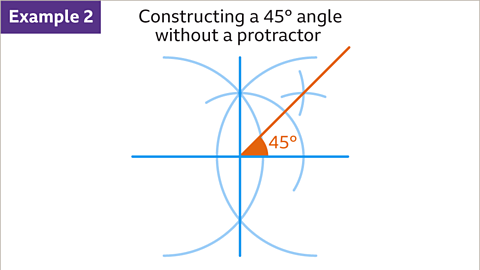
Image caption,
How to construct a 45° angle without a protractor
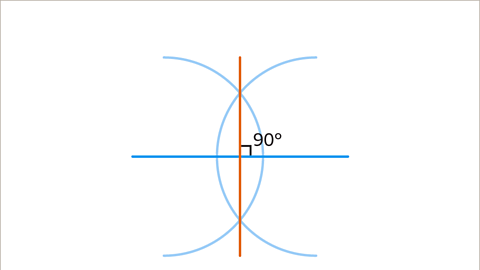
Image caption,
To construct a 45° angle, first construct a perpendicular bisector. When constructed accurately, this makes a 90° angle.
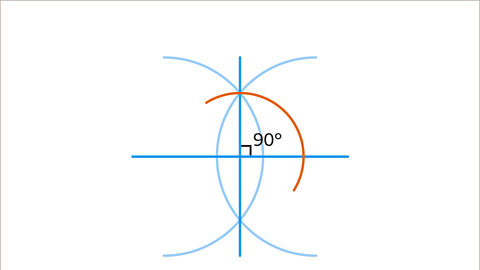
Image caption,
The 90° angle needs to be bisected. Draw an arc from the 90° angle.
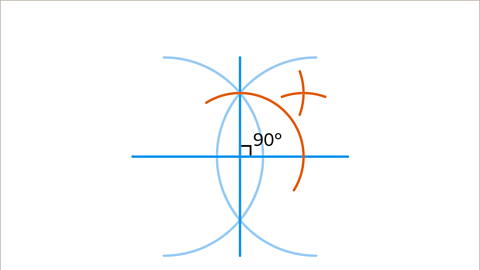
Image caption,
Draw two smaller arcs from each point of intersection, between the arc and the angle.
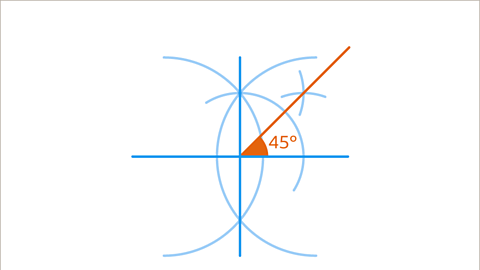
Image caption,
The two new arcs will intersect once. Draw a line from the first point to this intersection. If drawn accurately, this will make a 45° angle.

Question

How many arcs are needed to construct an angle bisector?

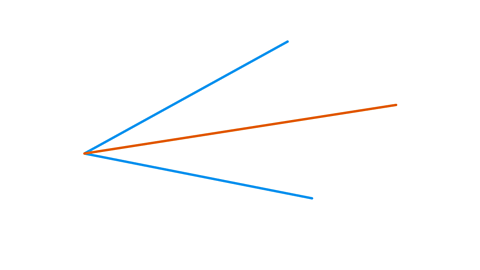
An image of two straight lines that meet at an angle on the left. A line representing the angle bisector has been drawn in orange. The lines that meet at an angle are coloured blue.

Practise bisecting lines and angles

Quiz

Practise your knowledge of bisecting angles and lines with this quiz. You may need a pen and paper to help you with your answers.

Real-life maths

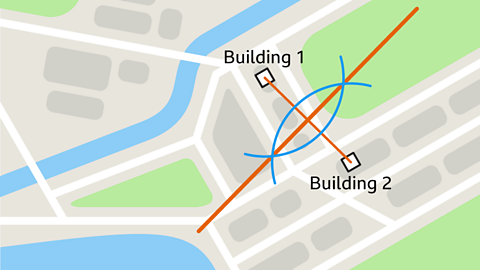
An image of a map. Two buildings, labelled building one and building two, have been marked on the map. The buildings have been joined by a line. The line has been bisected. — Image caption,
Town planners use perpendicular bisectors to find possible locations.

When deciding on the location of a new hospital, fire station or any other important building, town planners use perpendicular bisectors to find possible locations.

If the hospital must be the same distance from two different buildings, constructing a perpendicular bisector between them both will give all of the location options.