Key points about translation
A The movement of a shape from one place to another. The shape has the same orientation. is one of the four types of A transformation changes the position or size of a shape..
A translation moves a shape on a set of axes from one position to another.
The translation is defined using a A way of describing a translation using two numbers to describe horizontal and vertical displacements..
The new shape is congruent to the original shape.
The shape is not reflected or rotated, and the size of the shape does not change.
To understand translation, make sure you have a good understanding of naming and plotting coordinates.
How to describe a translation
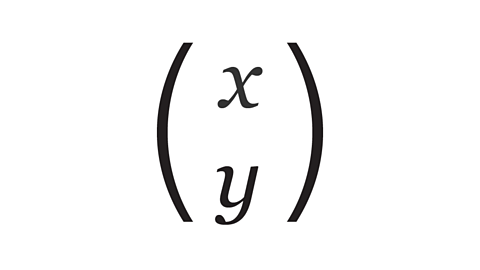
A translation is described using both horizontal and vertical displacements.
By counting squares on a set of axes, a translation can be worked out.
These displacements can then be represented using a column vector, as shown in the image.
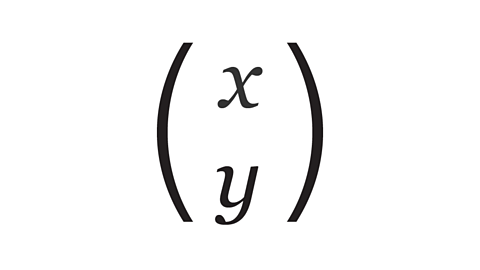
The 𝑥 value describes the horizontal displacement, or how much the shape moves right or left. A displacement to the right is a positive number and a displacement to the left is a negative number. A zero is used to indicate no horizontal movement.
The 𝑦 value describes the vertical displacement, or how much the shape moves up or down. An upward displacement is a positive number and a downward displacement is a negative number. A zero is used to indicate no vertical movement.
Using a The point at which two or more lines cross. The corner of a shape. The plural form is vertices. as a reference point helps track the translation of the shape.
Follow the worked example
GCSE exam-style questions
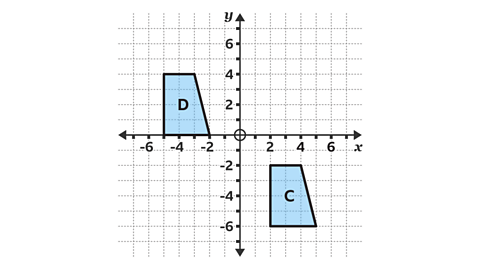
- What translation vector describes the transformation of shape C to shape D?
The correct translation vector is:
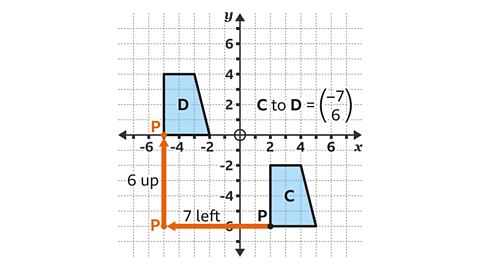
Reference point P moves 7 squares to the left and 6 squares up to the corresponding vertex (corner) of the new shape.
This is a horizontal displacement of −7 and a vertical displacement of 6.
This means shape D is a translation of this vector.
- What translation vector describes the transformation of shape K to shape L?
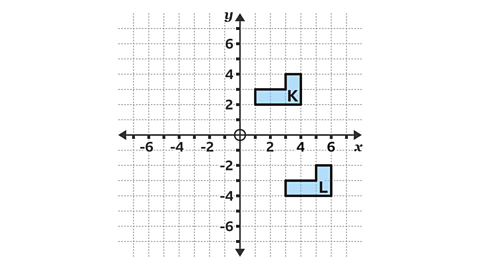
The correct translation vector is:
\(\begin{pmatrix}2 \\–6\end{pmatrix}\)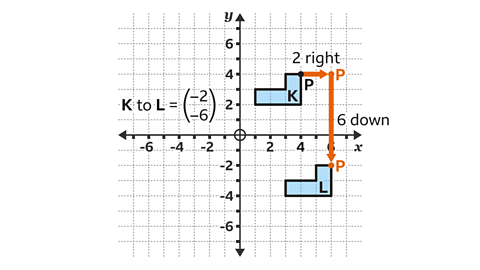
Reference point P moves 2 squares to the right and 6 squares down to the corresponding vertex (corner) of the new shape.
This is a horizontal displacement of 2 and a vertical displacement of −6.
This means shape L is a translation of this vector.
How to plot a translation
When given a The movement of a shape from one place to another. The shape has the same orientation., a plot of the shape in its new position can be worked out.
This is done by translating each The point at which two or more lines cross. The corner of a shape. The plural form is vertices. of the shape in turn. These points are then joined together to create the shape.
Alternatively, since the new shape is Shapes that are the same shape and size, they are identical. , just one vertex can be chosen as a reference point.
When this reference point is translated to the correct position, the whole congruent shape can be drawn, ensuring the length and direction of each side matches the original shape.
Watch the example below
Read the steps below to see the full method outlined.
To translate triangle A by the vector in the image:
The vector in the image means shape A is translated 3 squares to the right and 6 squares down. Vertex P, (−6, 4), is translated 3 squares horizontally to the right and 6 squares down. Its new coordinate is (−3, −2).
Vertex Q, (−2, 4), is also translated 3 squares horizontally to the right and 6 squares down. Its new coordinate is (1, −2).
Finally, vertex R, (−2, 6), is also translated 3 squares horizontally to the right and 6 squares down. Its new coordinate is (1, 0).
Joining the co-ordinates up, the new shape is finished. Label the new triangle B. Triangles A and B are congruent.
GCSE exam-style questions
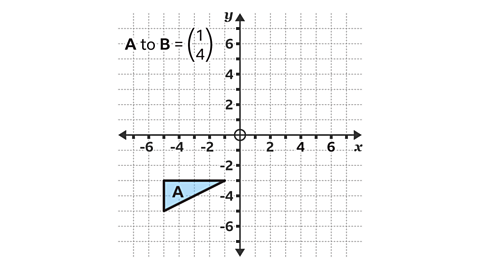
- Translate triangle A by the vector in the image.
Work out the position of the shape B using paper, a pencil and ruler.
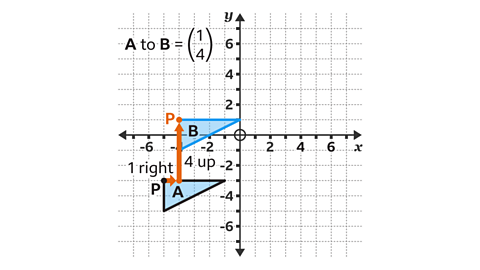
The correct position of shape B is shown.
The column vector translates the triangle one square to the right and four squares up.
A reference point, P, can be used to work out the position of the corresponding vertex (corner) of the new shape.
Vertex P, with coordinate (−5, −3), is translated to (−4, 1).
- Translate shape C by the vector in the image.
Work out the position of the shape D using paper, a pencil and ruler.
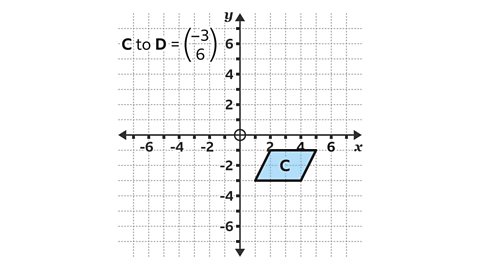
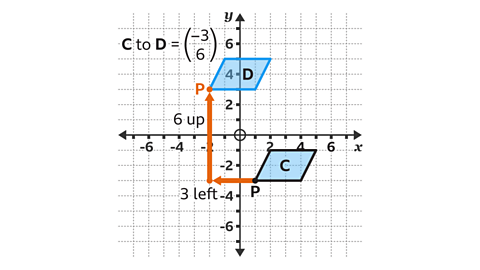
The column vector translates the shape three squares to the left and six squares up.
A reference point, P, can be used to work out the position of the corresponding vertex (corner) of the new shape.
Vertex P, with coordinate (1,−3) is translated to (−2,−3).
Check your understanding
Quiz – Translation
Practise what you've learned about translation with this quiz.
Now you've revised translation, why not learn about surface area of a prism?
More on Geometry and measure
Find out more by working through a topic
- count22 of 30
- count23 of 30
- count25 of 30
