Key points about surface area of a prism

The surface area of a 3D shape is the total area of all the faceOne of the flat surfaces of a solid shape. of the shape, measured in square units, including cm² and m².
The net of a 3D shape is what a shape looks like when opened into a 2D shape. The net can help to show the areas of each face that make up the surface area of a shape.
The same units are needed for the measurements of lengths used when finding areas, eg to work in centimetres a 1·2 m measurement would have to be converted to 120 cm.
Make sure you are confident in finding the area of a variety of shapes, as this can help when working out the surface area of 3D shapes.
How to calculate the surface area from a 3D diagram
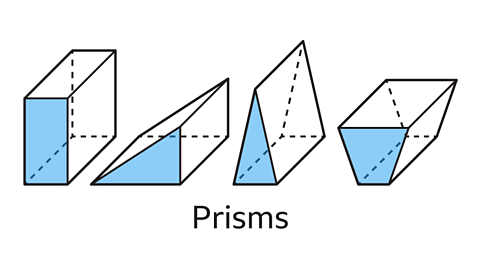
A prismA 3D shape with a uniform polygon cross-section. is a three-dimensional (3D) shape that has the same cross-sectionThe face that results from slicing through a solid shape. throughout its length.
The cross section is a polygon.
Find the surface areaThe total area of all the faces of a 3D shape. Measured in square units, such as cm² and m². of a prism by calculating the area of the two congruentShapes that are the same shape and size, they are identical. cross-sections and adding it to the area of the other rectangular faceOne of the flat surfaces of a solid shape. .
Find the surface area of a cuboid, a rectangular prism, by applying the formula:
𝑆𝐴 = 2𝑙𝑤 + 2ℎ𝑤 + 2ℎ𝑙
- 𝑆𝐴 is the surface area of the cuboid.
- 𝑙 is the length of the cuboid.
- 𝑤 is the width of the cuboid.
- ℎ is the height of the cuboid.
Find out more below, along with a worked example

Using the formula
Follow this additional example on calculating the surface area of a cuboid using the formula.
In this cuboid, the length measures 80 cm, the width measures 4 m and the height measures 5 m.
Work out the surface area of this cuboid.
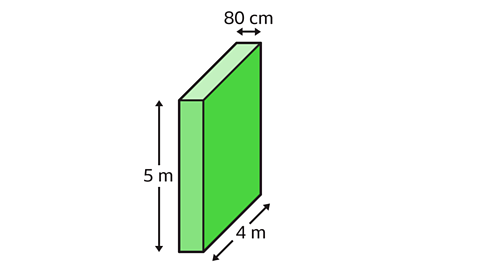
In this cuboid the length measures 80 cm, the width measures 4 m and the height measures 5 m.
When finding surface areas the measurements of lengths used must be in the same units.
Divide by 100 to convert the length measured in centimetres into metres:
80 cm = 0.8 m.
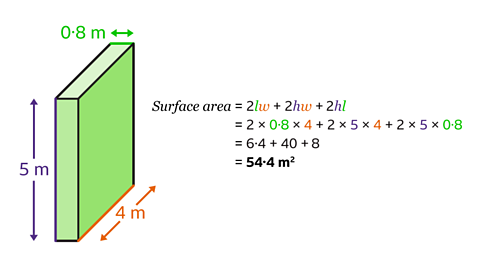
Using the formula, find the surface area by substituting the values for 𝑙,𝑤 and ℎ.
Surface area = 2 × 0·8 x 4 + 2 × 5 × 4 + 2 × 5 × 0·8 = 54·4
The surface area of the cuboid is 54·4 m² .
GCSE exam-style questions
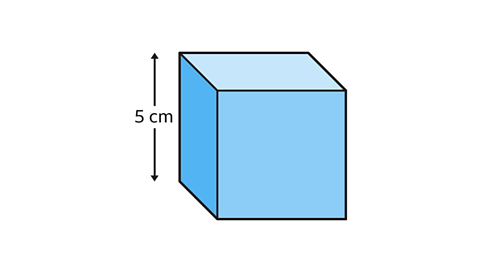
- Calculate the surface area of the cube.
The surface area of the cube is 150 cm².

A cube is a particular type of cuboid where all of the dimensions are equal in size.
The length, width and height all measure 5 cm.
Each of the six faces is a square.
Find the area of each face by multiplying the length and width.
The area of each face is 5 × 5 = 25 m².
To find the surface area of the cube, multiply the area of one face by 6.
25 × 6 = 150
- A triangular prism has a cross-section that is an equilateral triangle.
The area of the cross-section is 10·8 cm².
Calculate the total surface area of the prism.
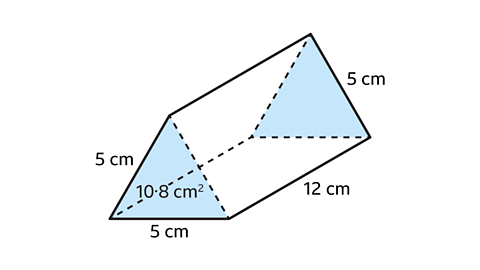
The surface area of the prism is 201·6 cm².
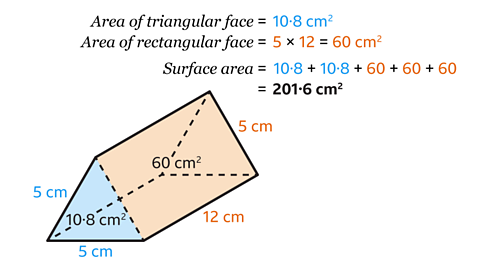
The triangular prism is made up of five faces. There are two congruent triangular faces and three identical rectangular faces.
The area of the triangle is given. Each triangle has an area of 10·8 cm².
- Find the area of a rectangle by multiplying the length and width.
The area of each rectangle is 5 × 12 = 60 cm².
- To find the surface area of the prism, add up the areas of the five faces.
10·8 + 10·8 + 60 + 60 + 60 = 201·6
How to calculate the surface area from a net
A netA group of joined 2D shapes which fold to form a 3D shape. can be used to help visualise the areas of each face that make up the surface area of a shape.
To calculate the surface area, first find the area of each face, then add up the areas of the individual faces.
Find out more below, along with a worked example
GCSE exam-style questions
- The net of a triangular prism is shown on a centimetre square grid.
What is the surface area of the prism?
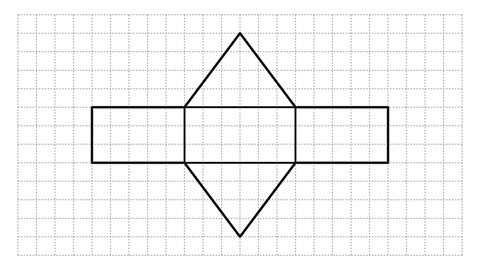
The surface area of the prism is 72 cm².
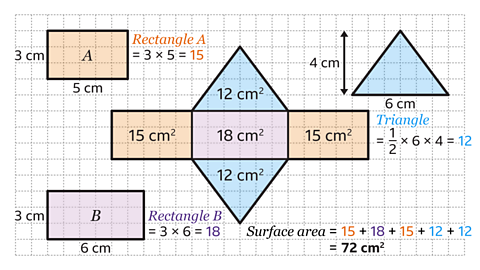
This triangular prism is made up of five faces. There are two congruent triangular faces and three rectangular faces.
The rectangular faces to the left and right of the net are the same size.
Calculate the area of a rectangle by multiplying the length and width.
- The area of rectangle A is 3 × 5 = 15 cm².
- The area of rectangle B is 3 × 6 = 18 cm².
Calculate the area of a triangle by using the formula \(𝐴 = \frac{1}{2}𝑏ℎ\)
- The area of each triangle is \(\frac{1}{2}\) × 6 × 4 = 12
Calculate the surface area of the prism, by adding up the areas of the five faces.
15 + 18 + 15 + 12 + 12 = 72
- What is the surface area of the prism?
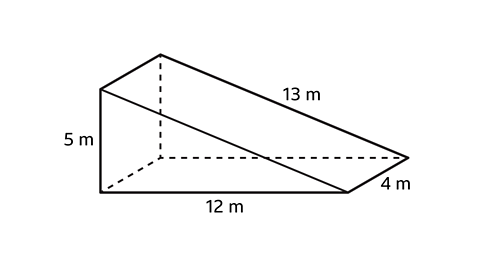
The surface area of the prism is 180 m².
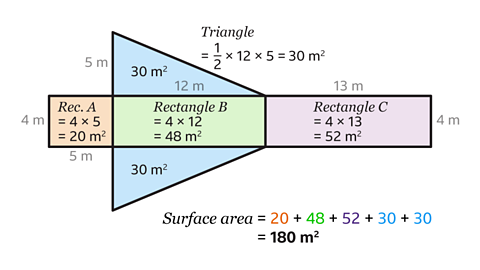
This triangular prism is made up of five faces. There are two congruent triangular faces and three rectangular faces.
Calculate the area of each rectangle by multiplying the length and width.
The area of rectangle A is 4 × 5 = 20 m².
The area of a rectangle B is 4 × 12 = 48 m².
The area of rectangle C is 4 × 13 = 52 m².
Calculate the area of a triangle using the formula
𝐴 = \(\frac{1}{2}𝑏ℎ \)
- The area of each triangle is \(\frac{1}{2}\) × 12 × 5 = 30
- To find the surface area of the prism add up the areas of the five faces.
20 + 48 + 52 + 30 + 30 = 180
Calculate the surface area of a cylinder
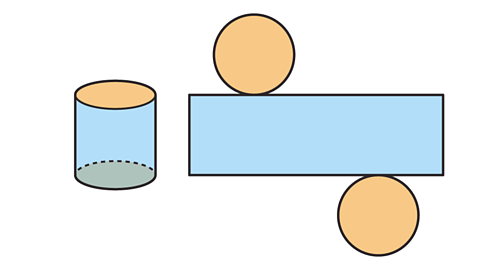
A cylinderA 3D shape with a constant circular cross-section across its length. is made up of two congruent circles and a rectangle.
Calculate the surface area by adding together the areas of the two circles and the rectangle.
Use the following formula to calculate the surface area of a cylinder:
𝑆𝐴 = 2π𝑟² + 2π𝑟ℎ
- 𝑆𝐴 is the surface area of the cylinder.
- 𝑟 is the radius of the circular face.
- ℎ is the height of the cylinder.
Find out more below, along with a worked example

GCSE exam-style questions
- Find the volume of the cylinder in terms of π.
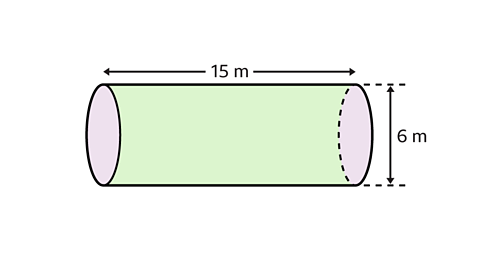
The total surface area of the cylinder is 108π m².
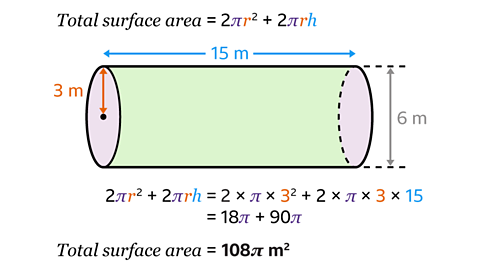
- The diameter of the circular cross-section is 6 m.
- The radius is half of the diameter. The radius of the circular cross-section is 3 m.
- The length of the cylinder is 15 m. The length is also the height of the cylinder.
Substitute the values of 𝑟 = 3 and ℎ = 15 into 2π𝑟² + 2π𝑟ℎ and work out the calculation.
- Surface area = 2 × π × 3² + 2 × π × 3 × 15
- Surface area = 18π + 90π
- Surface area = 108π
The total surface area of the cylinder is 108π m².
- The surface area of the cylinder is 320π cm².
Calculate 𝑥.
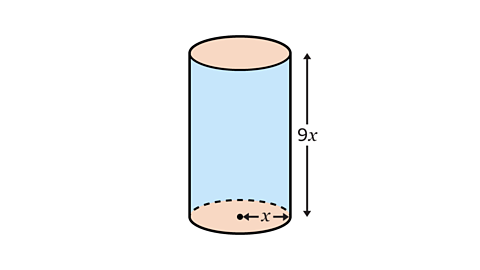
𝑥 = 4 cm

The value of 𝑥 can be calculated by setting up and solving an equation.
- First, find an expression for the surface area of the cylinder.
The radius of the circular cross-section is 𝑥 cm. The height of the cylinder is 9𝑥 cm.
Substitute the values of 𝑟 = 𝑥 and ℎ = 9𝑥 into 2π𝑟² + 2π𝑟ℎ and simplify the expression.
- Surface area = 2 × π × 𝑥² + 2 × π × 𝑥 × 9𝑥
- Surface area = 2𝑥²π + 18𝑥²π
- Surface area = 20𝑥²π
The given surface area is 320π cm² which must equal the expression 20𝑥²π.
To work out the value of 𝑥, divide each side by π which gives 20𝑥² = 320
To solve the equation, divide both sides by 20 which gives 𝑥² = 16
To find the value of 𝑥, work out the square root of 16.
The square root of 16 is 4 so 𝑥 = 4.
Check your understanding
Quiz – Surface area of a prism
Practise what you've learned about surface area of a prism with this quiz.
Now you've revised surface area of prisms, why not have a look at volume of a prism?
More on Geometry and measure
Find out more by working through a topic
- count13 of 35

- count14 of 35

- count15 of 35

- count16 of 35
