Key points about the alternate segment theorem, tangents and chords

Circles have different angle properties, described by theoremA mathematical rule.. This guide covers:
tangentA straight line which touches the edge of a circle or a curve at a single point. are perpendicularPerpendicular lines are at 90° (right-angles) to each other. to a radiusThe distance from the centre of the circle to the circumference. Plural of radius is radii. at the point of intersection
tangents either side of circle from a point are equal in length
the angle between a tangent and a chordA straight line joining two points on the circumference of a circle. is equal to the angle at the circumference in the alternate segmentAn area enclosed by a chord and an arc. (alternate segment theorem)
It is important to remember other angles rules, such as angles on a straight line add up to 180°, and to recognise angles in parallel lines.
Make sure you are confident in applying Pythagoras’ theorem before working with angles made by tangents and perpendiculars to chords.
When you are confident with the theorems in this guide, have a look at the guide on how to calculate angles with circles.
Tangent theorems
A tangent is a straight line which touches the circumferenceThe distance around a circle; its perimeter. of a circle at a single point.
A tangent makes a 90° angle or is perpendicular to the radius at that point.
The tangents from a point to a circle are equal in length.
Find out more below, along with a worked example
GCSE exam-style questions

- Line AB is a tangent to the circle at P.
Find 𝑥.
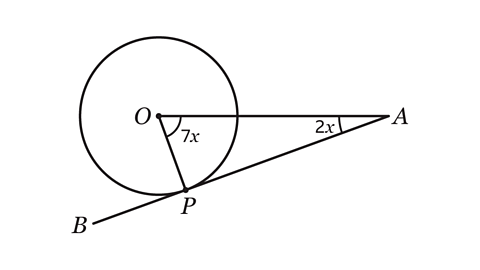
𝑥 = 10°
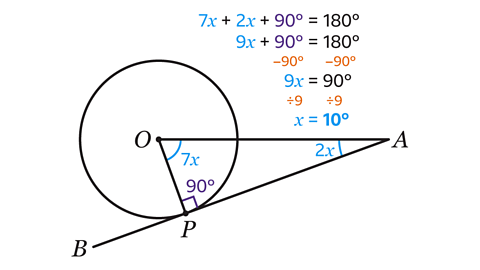
Line AB is a tangent to the circle at P.
Angle APO = 90°
Shape APO is a triangle.
The angles in a triangle add up to 180°.
- Form an equation by adding the angles and equating this to 180°.
7𝑥 + 2𝑥 + 90 = 180
- To find the value of 𝑥 first simplify the equation by collecting like terms.
9𝑥 + 90 = 180
- To solve the equation subtract 90 from both sides, which gives:
9𝑥 = 90
- Finally, divide both sides by 9, giving the answer, 𝑥 = 10°.
- Line EF is a tangent to the circle at X.
Line EG is a tangent to the circle at Y.
Angle FEG = 38°
Calculate the size of angle 𝑎.
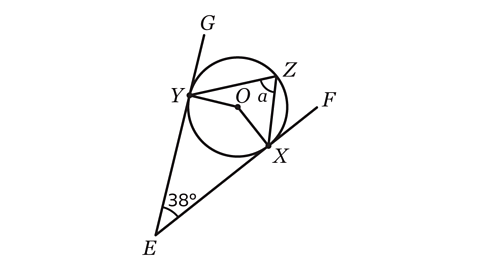
Angle 𝑎 = 71°
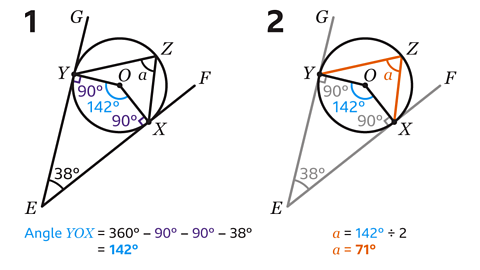
- Line EF is a tangent to the circle at X, hence angle EXO = 90°.
Line EG is a tangent to the circle at Y, hence angle EYO = 90°.
Shape EXOY is a quadrilateral.
The angles in a quadrilateral add up to 360°.
Calculate angle YOX by subtracting the three angles from 360°.
360 − 90 − 90 − 38 = 142
Angle YOX = 142°
- The angle at the centre of a circle is twice the angle at the circumference that is subtended by the same arc.
Angle 𝑎 is half the size of 142°.
142 ÷ 2 = 71
- Line GH is a tangent to the circle of radius 5 cm at X.
GX = 12 cm
Calculate the length of GO.
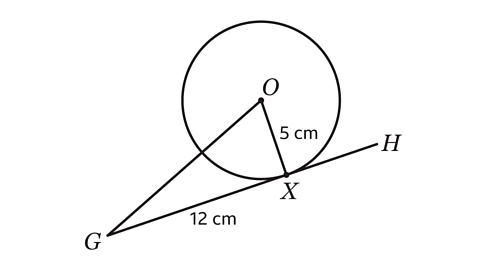
GO = 13 cm
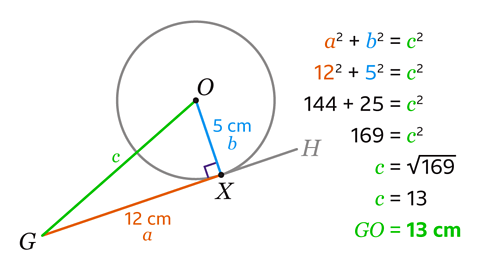
Since line GH is a tangent to the circle at X, angle GXO = 90°.
Shape GXO is a right-angled triangle.
The sides in a right-angled triangle satisfy Pythagoras’ theorem, 𝑎² + 𝑏² = 𝑐².
GO is the hypotenuse, so should be labelled as 𝑐.
GX can be labelled as 𝑎 and XO can be labelled as 𝑏.
Substitute these values into 𝑎² + 𝑏² = 𝑐² to give 122 + 52 = 𝑐².
12² is 144 and 5² is 25.
Adding the two squares together gives 𝑐² = 169.
To find 𝑐, the inverse of squaring is square rooting, so 𝑐 = √169 = 13.
What is the alternate segment theorem?
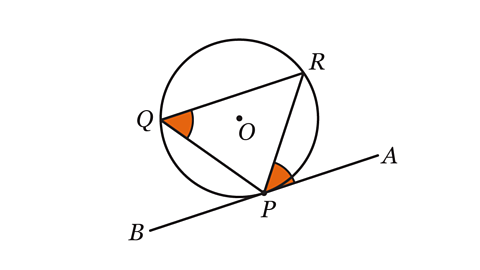
The alternate segment theorem states that the angle between a tangent and a chord is equal to the angle at the circumference in the alternate segment.
In the image to the right, angles RPA and PQR are in alternate segments.

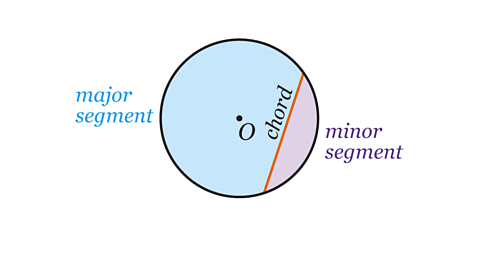
A chord is a straight line joining two points on the circumference of a circle.
It cuts a circle into two segments, a minor segment and a major segment.
The image to the left shows examples of alternate segments.
Find out more about the alternate segment theorem below
GCSE exam-style questions
- Line AB is a tangent to the circle at P.
Angle PRQ = 65°
Angle PQR = 58°
Calculate the size of angle 𝑥.
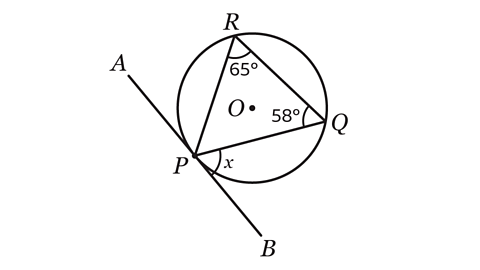
Angle 𝑥 = 65°
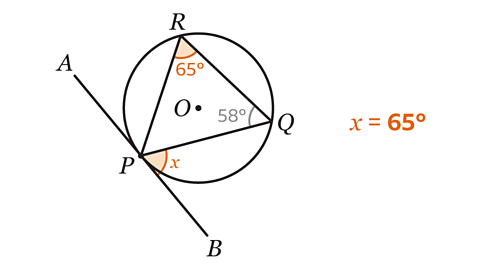
Using the alternate segment theorem, the angle between a tangent and a chord is equal to the angle at the circumference in the alternate segment.
Angle BPQ = Angle PRQ.
- Line AB is a tangent to the circle at X.
The length of line ZX is equal to the length of line ZY.
Angle BXZ = 64°
Calculate the size of angle 𝑤.
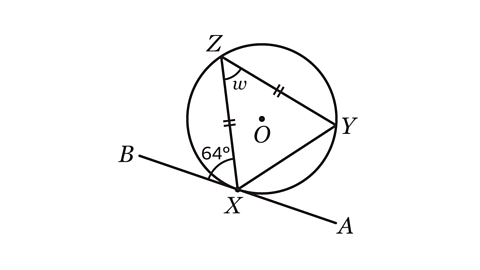
Angle 𝑤 = 52°
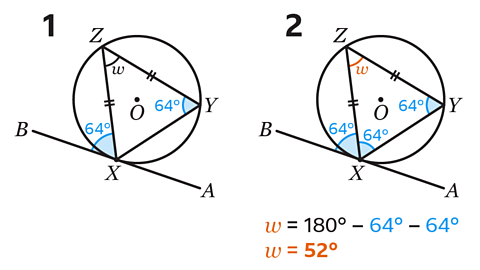
Using the alternate segment theorem, the angle between a tangent and a chord is equal to the angle at the circumference in the alternate segment.
Angle BXZ = Angle XYZ = 64°.
The equal sides, indicated, show that triangle XYZ is isosceles.
An isosceles triangle also has two equal angles.
Angle XYZ = Angle ZXY = 64°.
The angles in a triangle add up to 180°.
Angle 𝑤 can be calculated by subtracting the two angles from 180°.
180 − 64 − 64 = 52
- Line XY is a tangent to the circle at A.
Angle BAY = 48°
Calculate the size of angle 𝑗.
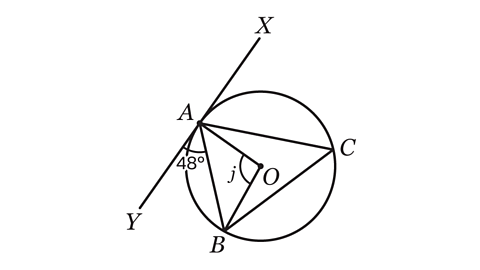
Angle 𝑗 = 96°
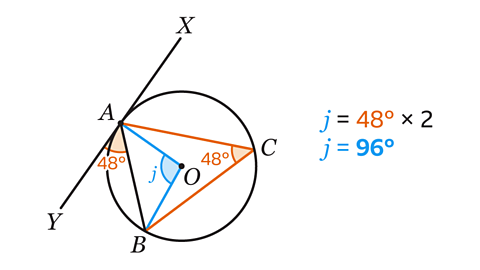
Using the alternate segment theorem, the angle between a tangent and a chord is equal to the angle at the circumference in the alternate segment.
Angle YAB = Angle ACB = 48°.
The angle at the centre of a circle is twice the angle at the circumference, that is subtended by the same arc.
Angle 𝑗 is twice the size of angle ACB.
48 × 2 = 96
- In the diagram, lines AD and BC are parallel.
Line PQ is a tangent to the circle at A.
Angle DAP = 47°
Angle BAQ = 31°
Calculate the size of angle 𝑦.
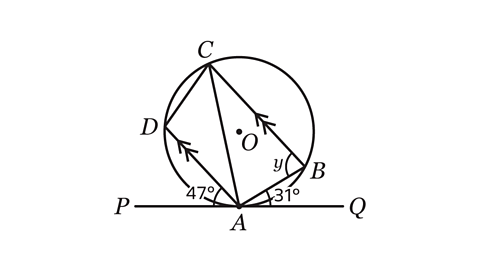
Angle 𝑦 = 78°
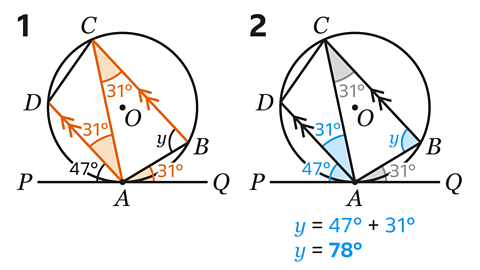
- Using the alternate segment theorem, the angle between a tangent and a chord is equal to the angle at the circumference in the alternate segment.
Angle QAB = Angle ACB = 31°.
Angle ACB and Angle CAD are alternate angles.
Alternate angles are equal.
Angle CAD = 31°.
- Similarly, using the alternate segment theorem, Angle PAC = Angle 𝑦.
To find angle PAC, add angles PAD and CAD.
47 + 31 = 78°
What are the properties of chords?
A chord is a straight line joining two points on the circumference of a circle.
When the perpendicular from the centre of a circle to a chord is drawn, the line bisectTo divide into two equal sections, cut in half. the chord.
Find out more below, along with a worked example
GCSE exam-style questions
- The circle centred at O has a radius, OR, which bisects line BC at X.
Angle BOR = 33°
Calculate the size of angle 𝑦.
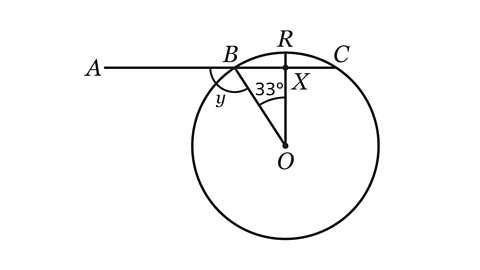
Angle 𝑦 = 123°.
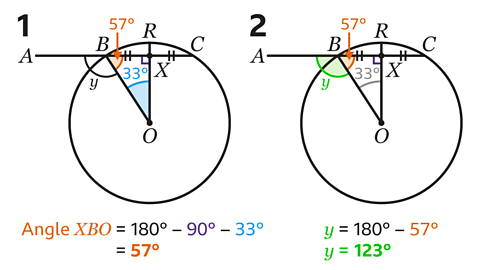
Since the radius, OR, bisects the chord BC at X, it must be perpendicular.
Angle OXB = 90°.
Shape OXB is a triangle.
The angles in a triangle add up to 180°.
- Calculate angle RBO by subtracting the two angles from 180°.
180 − 90 − 33 = 57
Angle RBO = 57°.
The angles on a straight-line add up to 180°.
- Calculate angle 𝑦 by subtracting 57° from 180°.
180 − 57 = 123
- A circle with a radius of 5 cm has a line OX which bisects a chord, AB, of length 6 cm at X.
Calculate the length of OX.
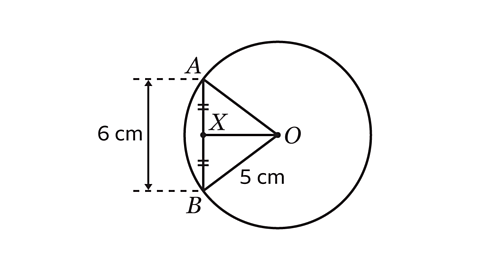
OX = 4 cm
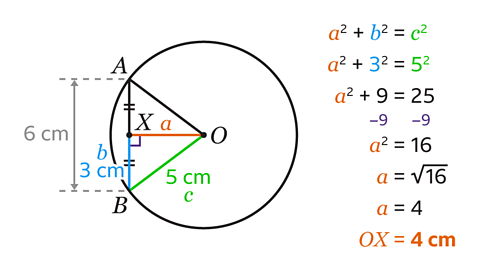
Since the line, OX , bisects the chord AB at X, it must be perpendicular.
Angle OXB = 90°. The length of XB is half the length of the chord.
6 ÷ 2 = 3
XB = 3 cm
Shape OXB is a right-angled triangle.
The sides in a right-angled triangle satisfy Pythagoras’ theorem, 𝑎² + 𝑏² = 𝑐².
OB is the hypotenuse, so is labelled 𝑐.
OX is labelled 𝑎.
XB is labelled 𝑏.
- Substitute these values into 𝑎² + 𝑏² = 𝑐² to give 𝑎² + 3² = 5².
5² is 25 and 3² is 9.
- Subtract the two squares to give 𝑎² = 16.
Find the inverse of 𝑎 by square rooting, so
𝑎 = √16 = 4
OX = 4 cm
Check your understanding
Quiz – Using the alternate segment theorem, tangents and chords
Practise what you've learned about calculating using the alternate segment theorem, tangents and chords, with this quiz.
Now you've revised calculating with the alternate segment theorem, tangents and chords, why not look at area of circles and sectors?
More on Geometry and measure
Find out more by working through a topic
- count19 of 35

- count20 of 35

- count21 of 35

- count22 of 35
