Key points about the sine rule

The sine rule is a formulaA fact, rule, or principle that is expressed in terms of mathematical symbols. The plural of formula is formulae. used to find a missing side or angle in a triangle when one pair of opposite sides and angle is given, and one other side or angle is known.
The sine rule can be expressed in two forms:
Find an unknown side using
\(\frac{𝑎}{sin𝐴} \) = \(\frac{𝑏}{sin𝐵} \) = \(\frac{𝑐}{sin𝐶 } \)Find an unknown angle using
\(\frac{sin𝐴}{𝑎} \) = \(\frac{sin𝐵}{𝑏} \) = \(\frac{sin𝐶 }{𝑐} \)
Scientific calculators need to be used for trigonometry and should be in degrees mode. Often there is a small D or DEG at the top of the calculator screen. If not, go into the calculator settings to change the angle units to degrees.
To be successful with non-right-angled trigonometryA branch of mathematics which explores the relationships between sides and angles in a triangle., make sure you are confident in finding unknown sides and angles in right-angled triangles.
How to find an unknown side using the sine rule
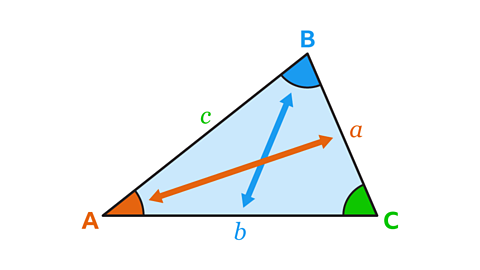
To use the sine rule to find an unknown side, one pair of opposite side and angle must be known. For example, angle 𝐴 and side 𝑎. The angle opposite the unknown side must also be known.
Label the angles and side of the triangle and use the formula \(\frac{𝑎}{sin𝐴} \) = \(\frac{𝑏}{sin𝐵} \) = \(\frac{𝑐}{sin𝐶 } \) to find the missing side.
The sine rule involves three equal ratios, but any calculation only requires two of the three parts.
If the vertices of the triangle are not called 𝐴, 𝐵 and 𝐶, it is common practice to rename them to assist with the substitutionThe process of replacing a letter (or variable) with a number. into the formula.

Follow the worked example below
GCSE exam-style questions

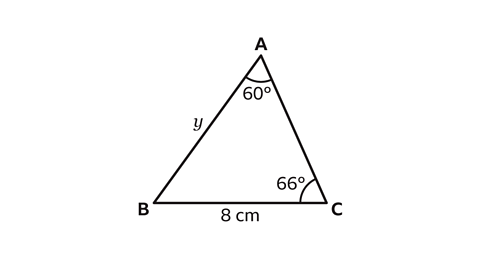
- Calculate the length of side 𝑦.
Give the answer to one decimal place.
𝑦 = 8·4 cm
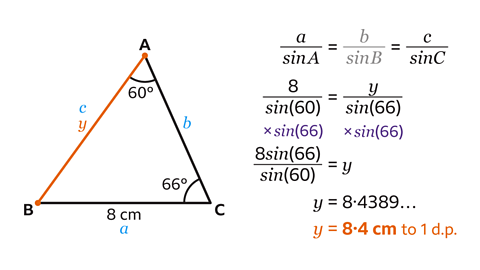
- Label the sides of the triangle.
The 8 cm side, opposite angle 𝐴, is called 𝑎.
The side labelled 𝑦, opposite angle 𝐶 is called 𝑐 and the unknown side, opposite angle 𝐵, is called 𝑏.
Since neither side 𝑏 nor angle 𝐵 is known, this is the portion of the sine rule formula that will not be used.
Substitute the values of 𝐴, 𝐶, 𝑎 and 𝑐 into the formula to give
\(\frac{8}{sin(60)} \) = \(\frac{𝑦}{sin(66)} \)Rearrange the equation to make 𝑦 the subject.
Find the value of 𝑦 by multiplying both sides of the equation by sin(66).
This gives \(\frac{8sin(60)}{sin(60)} \) = 𝑦.
- Type \(\frac{8sin(60)}{sin(60)} \) into a scientific calculator.
Usually, the calculator will automatically open a bracket after pressing the sin button.
Remember to close the bracket each time after typing in the angle.
This gives 𝑦 = 8·4389…
Rounded to 1 decimal place, 𝑦 = 8·4 cm.
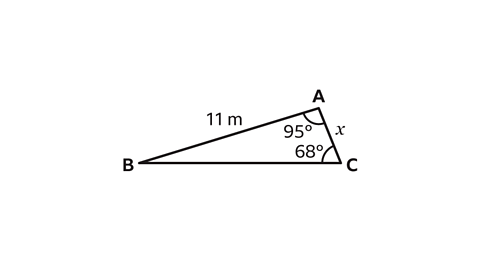
- Calculate the length of side 𝑥.
Give the answer to one decimal place.
𝑥 = 3·5 m
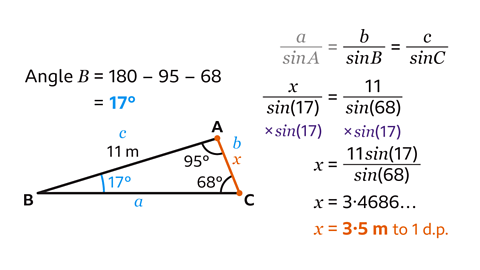
- Label the sides of the triangle.
The 11 m side, opposite angle 𝐶, is called 𝑐.
The side labelled 𝑥, opposite angle 𝐵, is called 𝑏 and the unknown side, opposite angle 𝐴, is called 𝑎.
- To use the sine rule, the angle opposite 𝑥 must be calculated.
The angles in a triangle add up to 180°.
180 – 96 – 68 = 17
Angle 𝐵 = 17°.
Substitute the values of 𝐵, 𝐶, 𝑏 and 𝑐 into the formula to give
\(\frac{𝑥}{sin(17)} \) = \(\frac{11}{sin(68)} \)Rearrange the equation to make 𝑥 the subject.
Find the value of 𝑥 by multiplying both sides of the equation by sin(17).
This gives 𝑥 = \(\frac{11sin(17)}{sin(68)} \).
- Type 11sin(17) ÷ sin(68) into a scientific calculator.
This gives 𝑥 = 3·4686…
Rounded to 1 decimal place, 𝑥 = 3·5 m.
- Calculate the length of side 𝑃𝑄.
Give the answer to one decimal place.
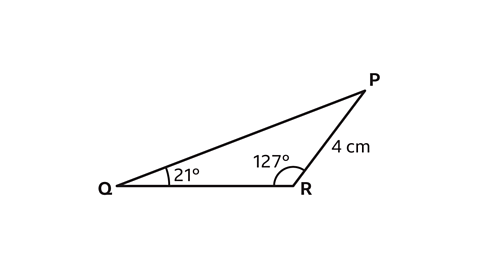
𝑃𝑄 = 8·9 cm
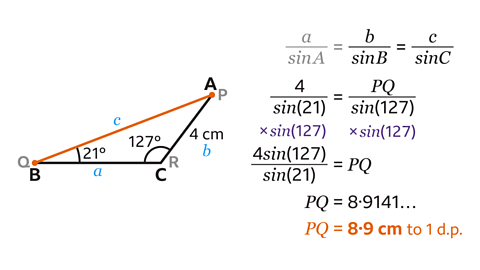
1.Label the sides of the triangle.
Since the vertices are not called 𝐴,𝐵 and 𝐶, let vertex 𝑃 be 𝐴, 𝑄 be 𝐵 and 𝑅 be 𝐶.
The 4 cm side, opposite angle 𝐵, is called 𝑏.
The side 𝑃𝑄 (or 𝐴𝐵), opposite angle 𝐶, is called 𝑐 and the unknown side, opposite angle 𝐴 is called 𝑎.
Since neither side 𝑎 nor angle 𝐴 is known, this is the portion of the sine rule formula that will not be used.
Substitute the values of 𝐵, 𝐶, 𝑏 and 𝑐 into the formula to give
\(\frac{4}{sin(21)} \) = \(\frac{𝑃𝑄}{sin(127)} \)Rearrange the equation to make 𝑃𝑄 the subject.
Multiply both sides of the equation by sin(127) to find the value of 𝑃𝑄.
This gives \(\frac{4sin(127)}{sin(21)} \) = 𝑃𝑄.
- Type 4sin(127) ÷ sin(21) into a scientific calculator.
This gives 𝑃𝑄 = 8·9141…
The length of 𝑃𝑄, rounded to 1 decimal place, = 8·9 cm.
How to find an unknown angle using the sine rule
To use the sine rule to find an unknown angle, an angle and its opposite side must be known. For example, angle 𝐴 and side 𝑎.
The length of the side opposite the unknown angle must also be known.
Label the angles and sides of the triangle and use the formula
\(\frac{sin𝐴}{𝑎} \) = \(\frac{sin𝐵}{𝑏} \) = \(\frac{sin𝐶 }{𝑐} \) to find the missing angle.
As with the previous application of the sine rule, only two parts of the formula will be used in the calculation.
Remember, when finding angles using trigonometry the inverseThe opposite of a mathematical process. trigonometric functions are used.
Follow the worked example below
GCSE exam-style questions
- Calculate the size of angle 𝐴.
Give the answer to one decimal place.
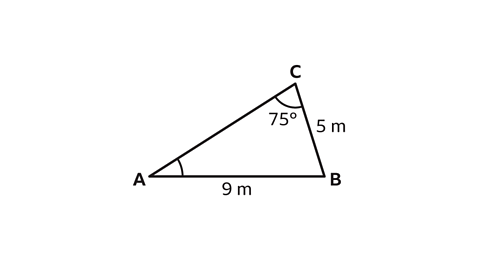
𝐴 = 32·5°
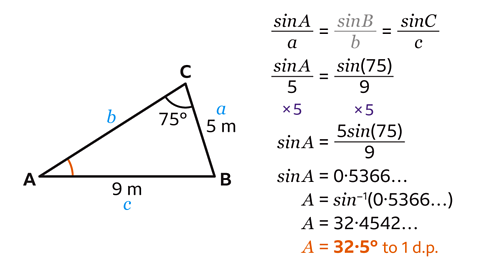
- Label the sides of the triangle.
The 9 m sides, opposite angle 𝐶, is called 𝑐.
The 5 m side, opposite angle 𝐴, is called 𝑎, and the unknown side, opposite angle 𝐵 is called 𝑏.
Since neither side 𝑏, nor angle 𝐵 is known, this is the portion of the sine rule formula that will not be used.
Substitute the values of 𝐴, 𝐶, 𝑎 and 𝑐 into the formula to give\(\frac{sin𝐴}{5} \) = \(\frac{sin(75)}{9} \).
Rearrange the equation to make sin𝐴 the subject.
Multiply both sides of the equation by 5 to find the value of sin𝐴. This gives sin𝐴 = \(\frac{5sin(75)}{9} \).
- Type 5sin(75) ÷ 9 into a scientific calculator.
This is the value of sin𝐴.
This gives sin𝐴 = 0·5366…
It is important not to round the number at this stage.
- Calculate angle 𝐴, using the inverse function of sine.
𝐴 = sin⁻¹(0·5366…)
Press 'Shift' then 'sin' to write sin⁻¹ on a scientific calculator.
- Next, use the 'ANS' button which will substitute the value of the previous decimal.
This gives 𝐴 = 32·4542…
Rounded to 1 decimal place, 𝐴 = 32·5°.
- Calculate the size of angle 𝑋𝑍𝑌.
Give the answer to one decimal place.
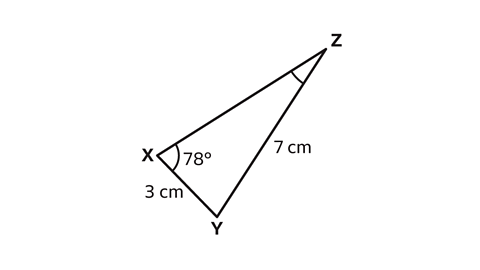
Angle 𝑋𝑍𝑌 = 24·8°
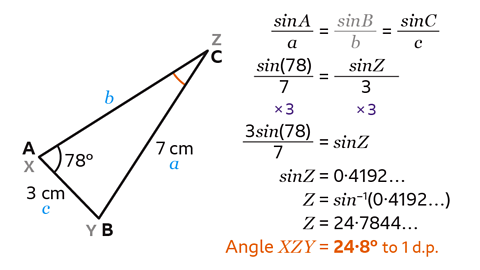
- Label the sides of the triangle.
Since the vertices are not called 𝐴,𝐵 and 𝐶, let vertex 𝑋 be 𝐴, 𝑌 be 𝐵 and 𝑍 be 𝐶.
The 3 cm side, opposite angle 𝐶, is called 𝑐.
The 7 cm side, opposite angle 𝐴, is called 𝑎, and the unknown side, opposite angle 𝐵, is called 𝑏.
Since neither side 𝑏 nor angle 𝐵 is known, this is the portion of the sine rule formula that will not be used.
Substitute the values of 𝑋, 𝑍, 𝑥 and 𝑧 into the formula to give \(\frac{sin(78)}{7} = \frac{sin𝑍}{3} \).
Rearrange the equation to make sin𝑍 the subject.
Multiply both sides of the equation by 3 to find the value of sin𝑍.
This gives \(\frac{3sin(78)}{7} = sin𝑍\).
- Type 3sin(78) ÷ 7 into a scientific calculator.
This is the value of sin𝑍.
This gives sin𝑍 = 0·4192…
It is important not to round the number at this stage.
- Calculate angle 𝑍, using the inverse function of sine.
𝑍 = sin⁻¹ (0·4192…).
Press 'Shift' then 'sin' to write sin⁻¹ on a scientific calculator.
- Next, use the 'ANS' button which will substitute the value of the previous decimal.
Remember to close the brackets.
This gives 𝑍 = 24·7844…
Rounded to 1 decimal place, angle 𝑋𝑍𝑌 = 24·8°.
Check your understanding
Finding an unknown angle using the sine rule: the ambiguous case
When calculating an angle using the sine rule, sometimes there are two possible answers.
This is called the ambiguous case.
Find one answer, as before, using the formula
\(\frac{sin𝐴}{𝑎} \) = \(\frac{sin𝐵}{𝑏} \) = \(\frac{sin𝐶 }{𝑐} \).
The second answer is found by subtracting the first answer from 180°.
If the angles in the triangle do not exceed the angle sum of a triangle, 180°, the second answer can exist.

Follow the worked example below
GCSE exam-style questions
- Triangle 𝐴𝐵𝐶 has sides 𝐴𝐶 = 7 m, 𝐴𝐵 = 8 m and
angle 𝐵 = 55°.
Angle 𝐶 is obtuse.
Find the size of angle 𝐶.
Give the answer to one decimal place.
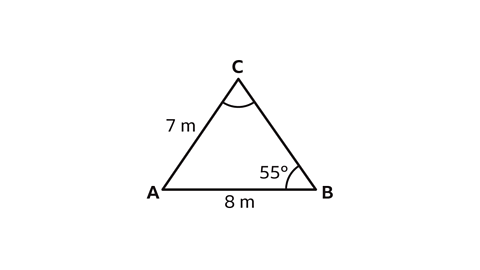
𝐶 = 110·6°
- Label the sides of the triangle.
The 8 m side, opposite angle 𝐶, is called 𝑐.
The 7 m side, opposite angle 𝐵, is called 𝑏, and the unknown side, opposite angle 𝐴, is called 𝑎.
Since neither side 𝑎 nor angle 𝐴 is known, this is the portion of the sine rule formula that will not be used.
Substitute the values of 𝐵, 𝐶, 𝑏 and 𝑐 into the formula to give \(\frac{sin(55)}{7} \) = \(\frac{sin𝐶}{8} \)
Rearrange the equation to make sin𝐶 the subject.
Find the value of sin𝐶 by multiplying both sides of the equation by 5.
This gives \(\frac{8sin(55)}{7} \) = sin𝐶.
- Type 8sin(55) ÷ 7 into a scientific calculator.
This is the value of sin𝐶.
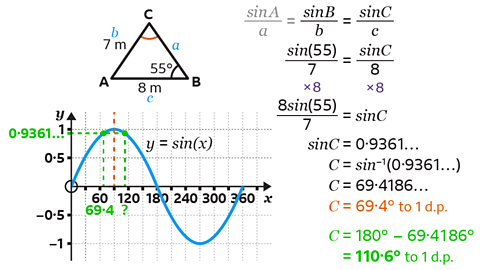
This gives sin𝐶 = 0·9361…
It is important not to round the number at this stage.
- Work out angle, 𝐶, using the inverse function of sine.
𝐶 = sin⁻¹ (0·9361…)
Press 'Shift' then 'sin' to write sin⁻¹ on a scientific calculator.
- Next use the ‘ANS’ button which will substitute the value of the previous decimal. Remember to close the brackets.
This gives 𝐶 = 69·4186…
Rounded to 1 decimal place, 𝐶 = 69·4°.
- This answer is acute so cannot be the required answer.
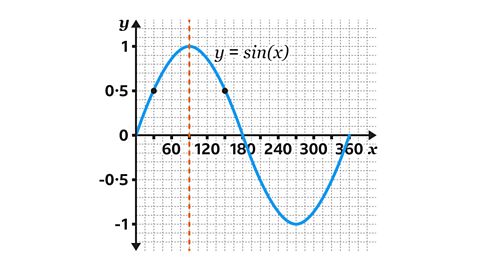
Use the graph of 𝑦 = sin(𝑥) to find the second answer.
The graph shows there is another angle which satisfies sin𝐶 = 0·9361…
Since the graph is symmetrical, the second answer is found by subtracting the first answer from 180°.
180 – 69·4186… = 110·5814…
Angle 𝐶 equals 110·6°, which is an obtuse angle.
- Triangle 𝑋𝑌𝑍 has side 𝑋𝑌 = 9 cm, 𝑌𝑍 = 6 cm and angle 𝑋 = 35°.
Work out the two possible values for angle 𝑍.
Give the answers to one decimal place.
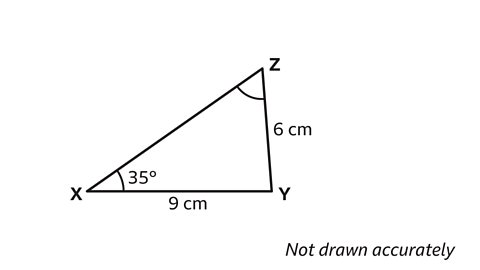
𝑋 = 59·4° and 120·6°
- Label the sides of the triangle.
Since the vertices are not called 𝐴, 𝐵 and 𝐶, let vertex 𝑋 be 𝐴, 𝑌 be 𝐵 and 𝑍 be 𝐶.
The 6 m side, opposite angle 𝑋, is called 𝑥.
The 9 m side, opposite angle 𝑍, is called 𝑧, and the unknown side, opposite angle 𝑌, is called 𝑦.
Since neither side 𝑦 nor angle 𝑌 is known, this is the portion of the sine rule formula that will not be used.
Substitute the values of 𝑋, 𝑍, 𝑥 and 𝑧 into the formula to give \(\frac{sin(35)}{6} = \frac{sin𝑍}{9} \).
Rearrange the equation to make sin𝑍 the subject.
Find the value of sin𝐶 by multiplying both sides of the equation by 5.
This gives \(\frac{9sin(35)}{6} \) = sin𝑍.
- Type 9sin(35) ÷ 6 into a scientific calculator.
This is the value of sin𝑍.
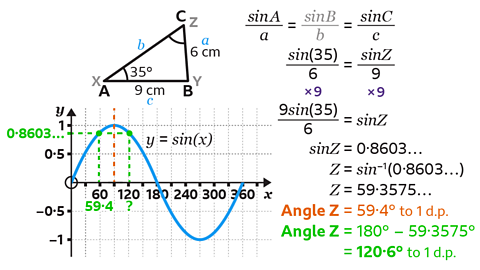
This gives sin𝑍 = 0·8603…
It is important not to round the number at this stage.
- Work out angle, 𝑍, using the inverse function of sine.
𝑍 = sin⁻¹ (0·8603…)
Press 'Shift' then 'sin' to write sin⁻¹ on a scientific calculator.
6, Next use the ‘ANS’ button which will substitute the value of the previous decimal. Remember to close the brackets.
This gives 𝑍 = 59·3575…
Rounded to 1 decimal place, 𝑍 = 59·4°.
- Use the graph of 𝑦 = sin(𝑥) to find the second answer.
The graph shows there is another angle which satisfies sin𝑍 = 0·8603…
Since the graph is symmetrical, the second answer is found by subtracting the first answer from 180°.
180 – 59·3575 = 120·6425
Angle 𝑍 can also be equal to 120·6°.
Quiz – Sine rule
Practise what you've learned about the sine rule with this quiz.
Now you've revised the sine rule, why not look at Calculating angles using circles?
More on Geometry and measure
Find out more by working through a topic
- count32 of 35

- count33 of 35

- count34 of 35

- count35 of 35
