6174 चे रहस्य: मराठी गणितज्ज्ञाने घातलेले कोडे, जे अजूनही बनले आहे एक गूढ

- Author, डेलिया व्हेंचुरा
- Role, बीबीसी न्युज मुंडो
गणिताच्या अथांग विश्वात अशा काही संख्या आहेत ज्या केवळ आकडे नसून एक रहस्य आहेत. 6174 ही त्यापैकीच एक! पहिल्या नजरेत ही संख्या अगदी सामान्य वाटू शकते, परंतु गेल्या 7 दशकांहून अधिक काळ या संख्येने जगभरातील मोठमोठ्या गणितज्ज्ञांना बुचकळ्यात पाडले आहे.
आता हा क्रमांक 6174 नीट लक्ष देऊन पाहा. पहिल्या नजरेत ही संख्या फारशी विशेष वाटत नाही, परंतु 1949 पासून ही गणितज्ज्ञांसाठी एक मोठे गूढ बनून राहिली आहे.
यामागचे कारण काय? हे समजून घेण्यासाठी या काही रंजक तथ्यांवर नजर टाकूया.
तुमच्या मनाप्रमाणे कोणतीही 4 अंकी संख्या निवडा, मात्र अट अशी आहे की कोणताही अंक पुन्हा येऊ नये, उदाहरणार्थ: 1234.
या अंकांना उतरत्या क्रमाने लिहा: 4321
आता त्यांना चढत्या क्रमाने लिहा: 1234
आता मोठ्या संख्येतून लहान संख्या वजा करा:
4321 - 1234
आता वजाबाकी करून जे उत्तर येईल, त्या संख्येसोबत पुन्हा पायरी 2, 3 आणि 4 ची पुनरावृत्ती करा.
चला, हे करून पाहूया
4321 - 1234 = 3087
या अंकांना उतरत्या क्रमाने मांडा: 8730
आता त्यांना चढत्या क्रमाने मांडा: 0378
आता मोठ्या संख्येतून लहान संख्या वजा करा:
8730 - 0378 = 8352
मिळालेल्या उत्तरासोबत वरील तिन्ही प्रक्रिया पुन्हा करा.
आता 8352 या संख्येसोबत हेच करून पाहूया
8532 - 2358 = 6174
आता 6174 सोबत याच आकडेमोडीची पुनरावृत्ती करूया, म्हणजेच अंक चढत्या आणि उतरत्या क्रमाने मांडून त्यांची वजाबाकी करूया-
7641 - 1467 = 6174
जसे की तुम्ही पाहू शकता, यानंतर ही प्रक्रिया पुन्हा करण्यात काही अर्थ नाही, कारण प्रत्येक वेळी तेच उत्तर मिळेल 6174.

फोटो स्रोत, Getty Images
या आकड्याची ही जादू खरोखरच थक्क करणारी आहे. पण तुम्हाला वाटू शकते की हा केवळ एक योगायोग आहे. तर चला, दुसऱ्या एखाद्या संख्येसोबत ही प्रक्रिया करून पाहूया. समजा, आपण 2005 ही संख्या घेऊया.
5200 - 0025 = 5175
7551 - 1557 = 5994
9954 - 4599 = 5355
5553 - 3555 = 1998
9981 - 1899 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174
तुम्ही स्वतः पाहू शकता, तुम्ही कोणतेही 4 अंक निवडले तरी अंतिम उत्तर 6174 हेच येते आणि एकदा हे उत्तर मिळाले की, त्याच प्रक्रियेने पुढेही तेच उत्तर येत राहते.
दत्तात्रेय रामचंद्र कापरेकर
भारतीय गणितज्ज्ञ दत्तात्रेय रामचंद्र कापरेकर (1905–1986) यांना संख्यांसोबत निरनिराळे प्रयोग करण्याची विलक्षण आवड होती. संख्यांवर सातत्याने केलेल्या अशा प्रयोगांमधूनच त्यांना 6174 या रहस्यमय संख्येचा शोध लागला.
सन 1949 मध्ये मद्रास येथे झालेल्या एका गणित संमेलनात कापरेकर यांनी जगाला या संख्येची ओळख करून दिली.
कापरेकर यांच्या या शोधाला सुरुवातीला उपेक्षेने पाहिले गेले, पण नंतर जगभरातील गणितज्ञांनी त्याचे महत्त्व मान्य केले. पुढे ही संख्या त्यांच्या नावानेच ओळखली जाऊ लागली आणि गणिताच्या विश्वात तिला एक विशेष स्थान प्राप्त झाले.
ते नेहमी म्हणायचे, "ज्याप्रमाणे नशेत धुंद राहण्यासाठी एखादा मद्यपी दारू पितो, अगदी तसेच माझे संख्यांच्या बाबतीत आहे."
त्यांचे शिक्षण मुंबई विद्यापीठातून झाले होते आणि देवळाली या छोट्या गावातील एका शाळेत शिक्षक म्हणून काम करत त्यांनी आपले आयुष्य व्यतीत केले.
सुरुवातीला त्यांच्या शोधाची थट्टा केली गेली आणि भारतीय गणितज्ञांनी तो फेटाळून लावला. असे असले तरी, अनेकदा त्यांना शाळा आणि महाविद्यालयांमध्ये त्यांच्या या आगळ्यावेगळ्या गणितीय पद्धतीवर विचार मांडण्यासाठी आमंत्रित केले जात असे.
हळूहळू त्यांच्या या शोधाची चर्चा भारतात आणि परदेशातही होऊ लागली. 1970 च्या दशकापर्यंत अमेरिकेतील प्रसिद्ध लेखक आणि गणिताचे जाणकार मार्टिन गार्डनर यांनी लोकप्रिय विज्ञान मासिक 'साइंटिफिक अमेरिका' मध्ये त्यांच्याबद्दल लेख लिहिला.
आज कापरेकर आणि त्यांच्या शोधाला जगभरात मान्यता मिळत असून अनेक गणितज्ज्ञ यावर संशोधन करत आहेत. ओसाका युनिव्हर्सिटीमधील इकॉनॉमिक्सचे प्रोफेसर युताका निशियामा म्हणतात, "6174 ही संख्या खरोखरच रहस्यांनी भरलेली आहे."
'+प्लस' (+plus) या ऑनलाइन मॅगझीनमध्ये निशियामा यांनी लिहिले आहे की, कशा प्रकारे त्यांनी 6174 ही संख्या मिळवण्यासाठी सर्व 4 अंकी संख्यांवर कॉम्प्युटरच्या साहाय्याने प्रयोग केले.
त्यांच्या प्रयोगाचा निष्कर्ष असा होता की, अशी कोणतीही 4 अंकी संख्या ज्यातील सर्व अंक वेगवेगळे आहेत, ती कापरेकर प्रक्रियेद्वारे जास्तीत जास्त 7 पायऱ्यांमध्ये 6174 पर्यंत पोहोचू शकते.
निशियामा यांच्या मते, "जर तुम्ही कापरेकर प्रक्रिया 7 वेळा करूनही 6174 पर्यंत पोहोचू शकला नाहीत, तर तुम्ही नक्कीच गणना करताना काहीतरी चूक केली आहे आणि तुम्ही पुन्हा प्रयत्न करायला हवा."
मॅजिक नंबर्स
अशा अनेक वैशिष्ट्यपूर्ण संख्या आहेत, ज्यांची नेमकी संख्या अजूनही माहित नाही. पण एक गोष्ट निश्चित आहे की, कापरेकर कॉन्स्टंट'प्रमाणेच 3 अंकी संख्यांसाठी देखील अशीच एक पद्धत अस्तित्वात आहे. समजा आपण 574 ही संख्या निवडली, तर चला त्यासोबत हीच प्रक्रिया करून पाहूया.
754 - 457 = 297
972 - 279 = 693
963 - 369 = 594
954 - 459 = 495
954 - 459 = 495
या प्रक्रियेनंतर अशा प्रकारे तुम्हाला 495 हा आणखी एक 'मॅजिक नंबर' प्राप्त होतो. गणितज्ञांचे असे मत आहे की, हे 'कॉन्स्टंट्स' म्हणजेच अपरिवर्तित संख्या या केवळ 3 आणि 4 अंकी संख्यांच्या बाबतीतच पाहायला मिळतात.
टेक्नीकलरमध्ये 6174
मुंबईच्या 'सीग्राम टेक्नॉलॉजीज फाउंडेशन'ने ग्रामीण आणि आदिवासी शाळांसाठी एक 'आयटी लर्निंग प्लॅटफॉर्म' विकसित केला आहे.
या संस्थेने 6174 या संख्येचा आपल्या अभ्यासक्रमात समावेश केला असून, त्यातील अंक रंगांच्या माध्यमातून प्रदर्शित करण्याचे ठरवले आहे.
फाउंडेशनचे संस्थापक गिरीश आराबाले यांनी बीबीसीला सांगितले की, ते मुलांमध्ये गणिताची आवड निर्माण करण्याचा प्रयत्न करत आहेत.
ते म्हणतात, "कापरेकर कॉन्स्टंट इतका रंजक आहे की, जेव्हा तुम्ही त्यांनी सांगितलेली पद्धत अवलंबता, तेव्हा ती तुम्हाला शेवटी अशा एका टप्प्यावर घेऊन जाते जिथे तुमच्या आनंदाला पारावार उरत नाही. पारंपारिक गणिती अभ्यासक्रम शिकताना असा अनुभव सहसा मिळत नाही."
फोटो स्रोत, Scigram Technologies Foundation
आराबाले यांच्या टीमने 6174 पर्यंत पोहोचण्यासाठी जेवढ्या पायऱ्या लागतात, त्या 'कलर कोड'च्या स्वरूपात प्रदर्शित करण्याचा निर्णय घेतला. त्यांना हे माहीत होते की, या मॅजिक नंबरपर्यंत पोहोचण्यासाठी 7 पेक्षा जास्त गणाना लागत नाहीत.
हे त्या कोडचा आधार बनले, ज्याला 'रॅसबेरी पाय' वर पुन्हा तयार केले जाऊ शकते. मुळात हा क्रेडिट कार्डच्या आकाराचा एक स्वस्त संगणक आहे, ज्याचा वापर प्रामुख्याने विज्ञान, तंत्रज्ञान, अभियांत्रिकी आणि गणिताच्या (STEM) शिक्षणात केला जातो.
फोटो स्रोत, Scigram Technologies Foundation
यानंतर विद्यार्थी, 'वोल्फ्रेम लँग्वेज' म्हणजे संगणकाची गणितीय भाषा वापरून याचे स्पष्टीकरण देऊ शकतात आणि सध्याच्या 4 अंकी असलेल्या 10,000 संख्यांचे विश्लेषण करू शकतात.
फोटो स्रोत, Scigram Technologies Foundation
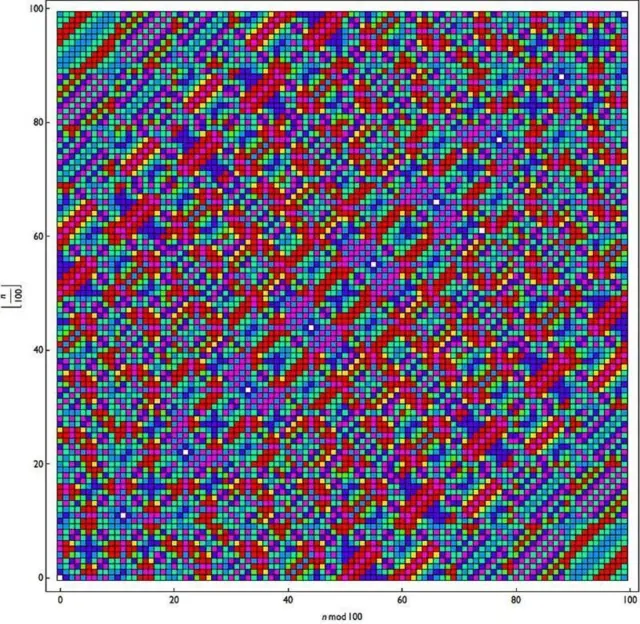
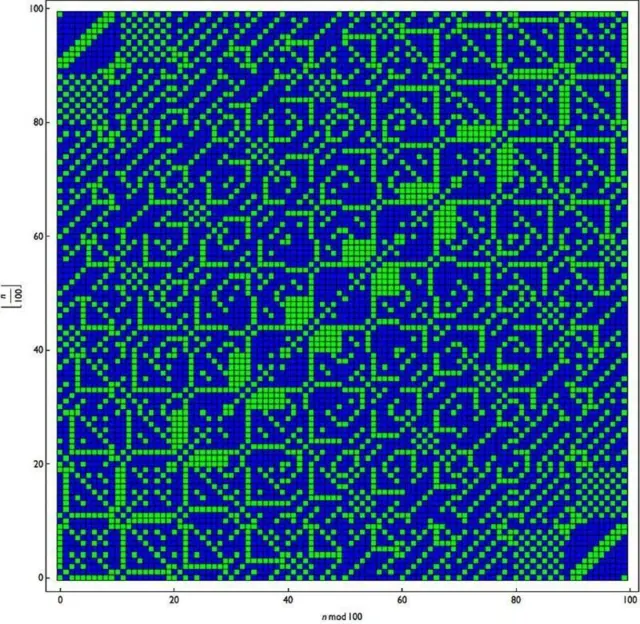
संख्या 6174 पर्यंत पोहोचण्यासाठी ही संगणकीय भाषा एक विशिष्ट पॅटर्न तयार करते आणि त्यातून एका बहुगुणी किंवा रंगीबेरंगी 'ग्रिड'ची निर्मिती होते.
एकदा का तुम्ही कोडींगला सुरुवात केली, आणि जर तुम्हाला विषम संख्या निळ्या रंगात आणि सम संख्या हिरव्या रंगात दिसू लागल्या, तर याचा नेमका अर्थ काय असेल?
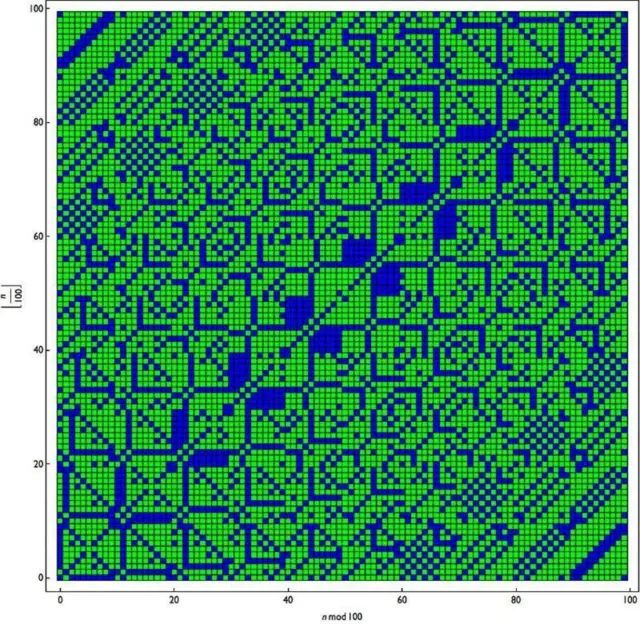
आणि जर तुम्ही मूळ संख्या हिरव्या रंगात आणि उर्वरित संख्या निळ्या रंगात दाखवल्या, तर तो पॅटर्न पूर्णपणे बदलला का?
कापरेकर कॉन्स्टंटचे योगदान केवळ खेळता खेळता गणित शिकण्यापुरते मर्यादित नाही.
तुम्ही कापरेकर नंबर'बद्दल देखील नक्कीच ऐकले असेल. यात अशी एक संख्या असते, जिचा वर्ग केल्यास मिळणाऱ्या उत्तराचे दोन भाग केले जाऊ शकतात आणि त्या दोन भागांची बेरीज केली असता मूळ संख्या पुन्हा प्राप्त होते.
हे आपण या उदाहरणावरून समजू शकतो-
297² = 88,209
88 + 209 = 297
(बीबीसीसाठी कलेक्टिव्ह न्यूजरूमचे प्रकाशन)