मैजिक नं. 6174, भारतीय गणितज्ञ की इस खोज ने दुनिया को हैरान कर रखा है

- Author, डेलिया वेंचुरा
- पदनाम, बीबीसी न्यूज़ मुंडो
संख्या 6174 को ध्यान से देखिए.
पहली नज़र में ये कुछ ख़ास नहीं दिखता लेकिन साल 1949 से यह गणितज्ञों के लिए एक पहेली बना हुआ है.
इसकी वजह क्या है? इसे समझने के लिए इन कुछ दिलचस्प तथ्यों को देखिएः
- कोई भी चार अंकों की संख्या अपने मन से चुनिए, लेकिन कोई भी अंक दोबारा नहीं आना चाहिए, उदाहरण के लिए 1234.
- इन्हें घटते क्रम में लिखिए: 4321
- अब इन्हें बढ़ते क्रम में लिखें: 1234
- अब बड़ी संख्या से छोटी संख्या को घटा दीजिए: 4321 - 1234
- अब नतीजे में मिली संख्या के साथ 2,3 और चार बिंदुओं को दोहराइए.
आईए इसे करके देखते हैंः
- 4321 - 1234 = 3087
- इन अंकों को घटते क्रम में रखें: 8730
- अब इन्हें बढ़ते क्रम में रखें: 0378
- अब बड़ी संख्या में से छोटी संख्या को घटा दीजिए: 8730 - 0378 = 8352
- नतीजे में मिली संख्या के साथ ऊपर की तीनों प्रक्रियाओं को दोहराईए.
अब संख्या 8352 के साथ यही करके देखते हैं-
- 8532 - 2358 = 6174
6174 के साथ इस प्रक्रिया को दुहराते हैं, यानी बढ़ते और घटते क्रम में रखने के बाद घटाएं.
7641 - 1467 = 6174
जैसा कि आप देख सकते हैं, इसके बाद फिर से ये प्रक्रिया दोहराने का कोई मतलब नहीं क्योंकि वही नतीजे मिलेंगे: 6174
लेकिन हो सकता है कि आप सोचें कि ये महज़ संयोग है. तो चलिए किसी दूसरे नंबर के साथ ये प्रक्रिया दोहराते हैं. मान लीजिए 2005 को लेते हैं.
- 5200 - 0025 = 5175
- 7551 - 1557 = 5994
- 9954 - 4599 = 5355
- 5553 - 3555 = 1998
- 9981 - 1899 = 8082
- 8820 - 0288 = 8532
- 8532 - 2358 = 6174
- 7641 - 1467 = 6174
आप ख़ुद देख सकते हैं, चाहे कोई भी चार अंक आप चुनें अंतिम नतीजा 6174 मिलता है, और इसके बाद उसी प्रक्रिया के साथ यही नतीजा मिलना जारी रहता है.
कैप्रेकर्स कांसटैंट

इमेज स्रोत, Getty Images
इस फ़ार्मूले को कैप्रेकर्स कांस्टैंट कहते हैं.
भारतीय गणितज्ञ दत्तात्रेय रामचंद्र काप्रेकर (1905-1986) को संख्याओं के साथ प्रयोग करना बेहद पसंद था और इसी प्रक्रिया में उनका परिचय इस रहस्यमयी संख्या 6174 से हुआ.
साल 1949 में मद्रास में हुए एक गणित सम्मेलन में काप्रेकर ने दुनिया को इस संख्या से परिचित कराया.
वो कहा करते थे, "जिस तरह मदहोश बने रहने के लिए एक शराबी शराब पीता है. संख्याओं के मामले में मेरे साथ भी बिल्कुल ऐसा ही है."
वो मुंबई विश्विद्यालय से पढ़े थे और मुंबई के देवलाली क़स्बे में एक स्कूल में पढ़ाते हुए उन्होंने अपनी ज़िंदगी गुज़ारी थी.
हालांकि उनकी खोज का मज़ाक़ उड़ागा गया और भारतीय गणितज्ञों ने इसे ख़ारिज कर दिया. अक्सर उन्हें स्कूल और कॉलेजों में उनके विशेष तरीक़े पर बात रखने के लिए बुलाया जाता था.
इमेज स्रोत, Getty Images
धीरे-धीरे उनकी खोज को लेकर भारत और विदेशों में चर्चा होने लगी और 1970 के दशक तक अमरीका के बेस्ट सेलिंग लेखक और गणित में रुचि रखने वाले मार्टिन गार्डर ने उनके बारे में एक लोकप्रिय साइंस मैग्ज़ीन 'साइंटिफ़िक अमेरिका' में उनके बारे में लिखा.
आज काप्रेकर और उनकी खोज को मान्यता मिल रही है और इस पर दुनिया भर के गणितज्ञ काम कर रहे हैं.
ओसाका यूनिवर्सिटी में इकोनॉमिक्स के प्रोफ़ेसर युताका निशियामा का कहना है, "संख्या 6174 वाक़ई बहुत रहस्यवादी संख्या है."
एक ऑनलाइन मैग्ज़ीन +प्लस में निशियामा ने लिखा कि कैसे उन्होंने संख्या 6174 को पाने के लिए सभी चार अंकों के साथ प्रयोग करने के लिए कम्प्यूटर का इस्तेमाल किया था.
उनका नतीजा था कि हर चार अंकों की संख्या, जिसमें सभी अंक अलग अलग हों, काप्रेकर की प्रक्रिया के तहत सात चरण में संख्या 6174 तक पहुंचा जा सकता है.
निशियामा के अनुसार, "अगर आप काप्रेकर की प्रक्रिया को सात बार दोहराने के बाद भी 6174 तक नहीं पहुंच पाते हैं तो आपने ज़रूर कोई ग़लती की है और आपको फिर से कोशिश करनी चाहिए."
मैजिक नंबर्स
लेकिन इस तरह के कई विशेष संख्याएं होती हैं, जिनकी ठीक ठीक संख्या पता नहीं है.
लेकिन इतना ज़रूर है कि काप्रेकर कॉन्स्टैंट की तरह ही तीन अंकों के लिए भी एक ऐसा ही तरीक़ा है.
मान लीजिए हमने एक संख्य चुना 574, आईए इसके साथ ही वही प्रक्रिया दुहराते हैं.
- 754 - 457 = 297
- 972 - 279 = 693
- 963 - 369 = 594
- 954 - 459 = 495
- 954 - 459 = 495
और इस तरह आपको हासिल होता है एक और मैजिक नंबर 495.
गणितज्ञों का कहना है कि ये कॉन्स्टैंट (अपरिवर्तित संख्याएं) केवल तीन और चार अंकों वाली संख्याओं के साथ ही मिलते हैं.
टेक्नीकलर में 6174

इमेज स्रोत, Getty Images
मुंबई की सीग्राम टेक्नोलॉजीज़ फ़ाउंडेशन ने ग्रामीण और आदिवासी स्कूलों के लिए आईटी लर्निंग प्लेटफ़ॉर्म विकसित किया है.
इसने 6174 संख्या को अपने विषय में शामिल किया और तय किया कि इसके अंकों को रंगों के साथ प्रदर्शित किया जाए.
फ़ाउंडेसन के संस्थापक गिरीश आराबाले ने बीबीसी को बताया कि बच्चों में वो गणित की रुचि पैदा करने की कोशिश करते हैं.
वो कहते हैं, "काप्रेकर कॉन्स्टैंट इतना आकर्षक है कि जब आप उसके बताए तरीक़े अपनाते हैं तो वो आपको अंत में एक ऐसे पल पर ले जाता है जहां आपकी ख़ुशी का ठिकाना नहीं रहता. ये ऐसा है कि परम्परागत गणित पाठ्यक्रम सीखते हुए नहीं मिल सकता."
आराबेल की टीम ने 6174 तक पहुंचने में जितने चरण लगते हैं उन्हें कलर कोड के रूप में प्रदर्शित करने का फैसला किया. वो इस बात को जानते थे कि मैजिक नंबर तक पहुंचने में सात गणना से अधिक नहीं लगता.
ये उस उस कोड का आधार बना, जिसे रैसपबेरी पाई पर रिक्रिएट किया जा सकता है. असल में ये सस्ता और क्रेडिट कार्ड के आकार का एक कम्प्यूटर होता है जोकि साइंस, टेक्नोलॉजी, इंजीनियरिंग और गणित की पढ़ाई में आम तौर पर इस्तेमाल किया जाता है.
इसके बाद छात्र, वोल्फ्रेम लैंगुएज (कम्प्यूटर की गणितीय भाषा) का इस्तेमाल करते हुए इसकी व्याख्या और मौजूदा चार अंकों वाले 10,000 नंबर के लिए विश्लेषण कर सकते हैं.
संख्या 6174 तक पहुंचने के लिए ये अपनाए गए एक पैटर्न बनाता है और इसे एक बहुरंगीय ग्रिड का निर्माण होता है.
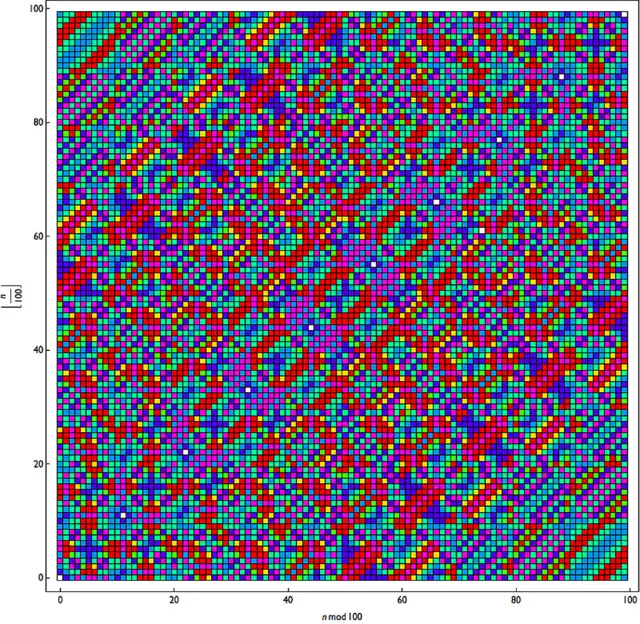
इमेज स्रोत, Scigram Technologies Foundation
एक बार जब आप कोडिंग शुरू करते हैं तो अगर आपको विषम संख्याएं नीले रंग में और सम संख्याएं हरे में दिखें तो इसका क्या मतलब होगा?

इमेज स्रोत, Scigram Technologies Foundation
और अगर आप प्राइम नंबर्स को हरे में दिखाते हैं और बाक़ी की संख्याएं नीले में दिखाई दें. क्या पैटर्न पूरी तरह बदला गया?
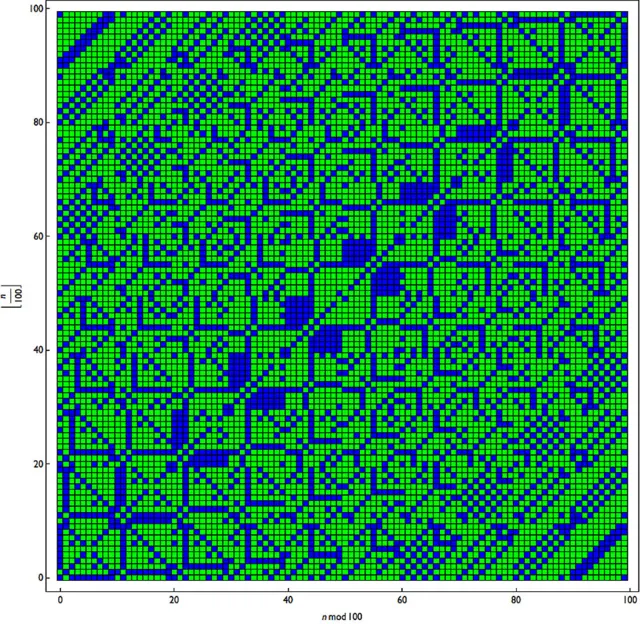
इमेज स्रोत, Scigram Technologies Foundation
खेल-खेल में गणित सीखना

इमेज स्रोत, Getty Images
काप्रेकर का कॉन्स्टैंट केवल खेल-खेल में गणित सीखने के तरीक़े में ही योगदान नहीं है.
आपने काप्रेकर नंबर के बारे में भी ज़रूर सुना होगा. इसमें एक संख्या है जिसका वर्ग किया जाए तो इसके नतीजे को दो हिस्सों में बांटा जा सकता है जिसका जोड़ मूल संख्या को दर्शाता है.
इसको कुछ इस तरह से समझ सकते हैंः
- 297² = 88,209
- 88 + 209 = 297
काप्रेकर संख्या का एक और अच्छा उदाहरण हैः9, 45, 55, 99, 703, 999, 2,223, 17,344, 538,461... इनके साथ साथ आप ख़ुद प्रयोग कर सकते हैं और देख सकते हैं कि क्या नतीजा मिलता है.
अगर नतीजे में मिली संख्या के अंकों को आप बराबर नहीं बांट पाते हैं जैसा कि 88209 के साथ है जिसमें पांच अंक हैं तो इसे पहले दो और फिर तीन अंक में विभाजित कर सकते हैं (88+209).
इसे काप्रेकर ऑपरेशन कहा जाता है. खेल-खेल में गणित सीखने का इससे बेहतर तरीक़ा और क्या हो सकता है!
(बीबीसी हिन्दी के एंड्रॉएड ऐप के लिए आप यहां क्लिक कर सकते हैं. आप हमें फ़ेसबुक, ट्विटर, इंस्टाग्राम और यूट्यूब पर फ़ॉलो भी कर सकते हैं.)