Key points
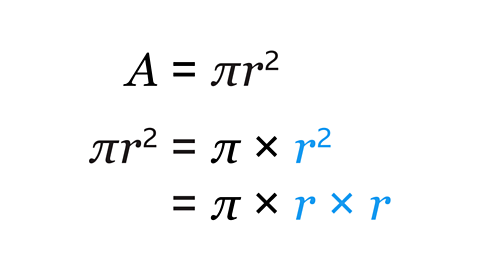
𝑨 = π𝒓² is the formulaA fact, rule, or principle that is expressed in words or in mathematical symbols. Plural: formulae. for finding the area of a circle. π is a constantA number or quantity that does not vary. and 𝒓 is the radiusThe distance from the centre of the circle to the circumference. of the circle.
The diameterThe distance across the circle, circumference to circumference, through its centre. of a circle is halved to give the radius. The value of π may be rounded to 3۰142 or 3۰14. The π button on a calculator is used in calculations. The area is given in square unitA square unit is defined as a metric unit used to measure area. For example, square metres (m²), square centimetres (cm²), square inches (In²) including cm² and m².
A scientific calculator may be set to show answers in surdAn irrational number. This includes the square roots that cannot be written as an exact decimal and special values like π. notation. Understanding how to use a calculator to convert between surd notation and the decimal equivalent is important.
The ability to round a number to a number of decimal places or to a number of significant figures is essential if answers are to be written to the correct degree of accuracy asked for in a question.
It may also be helpful to understand π (pi) and the circumference of a circle.
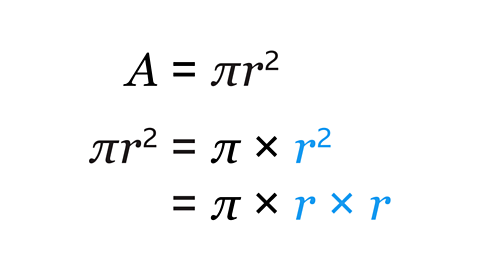
Calculating the area of a circle
To illustrate the formula for the area of a circle:
A circle can be cut into sectorA portion of a circle with a perimeter made up of two radii and an arc..
The sectors can be rearranged to form an approximateDescribing something that is not exact, but sufficiently close for it to be useful. rectangle shape. The more sectors the closer to a rectangle the shape will become.
The length of the rectangle is half the circumferenceThe distance around a circle; its perimeter., π𝒓. The width of the rectangle is the radius of the circle, 𝒓. The area of the rectangle is length × width, π𝒓 × 𝒓 = π𝒓².
The formula for the area of the circle is 𝑨 = π𝒓².
To work out the area of a circle:
Find the value of the radius. If the diameter is given, this must be halved.
Substitute the value of the radius into the formula for the area of a circle.
Multiply π by the square of the radius. This is the same as π × 𝒓 × 𝒓.
If necessary, round to the degree of accuracyHow precise a measurement is required, often shown as the number of decimal places or significant digits..
If using a scientific calculator, use the S
⇔
D button to convert a value given in terms of π to a decimal.
Example
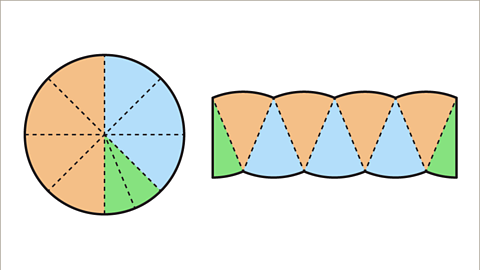
Image caption, A circle can be cut into sectors and rearranged into an approximate rectangle.
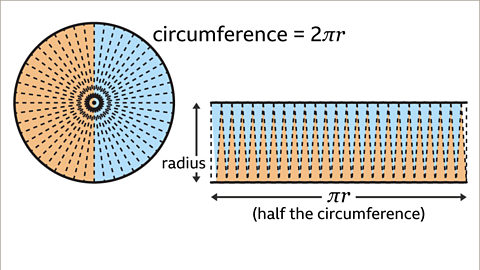
Image caption, The more sectors the better the rectangle approximation. The length of the rectangle is half of the circumference. C = 2π𝒓, so the length is π𝒓. This is π × 𝒓. The width of the approximate rectangle is the radius.
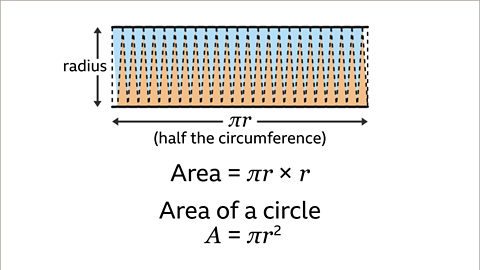
Image caption, The area of the rectangle is length × width. This is πr × 𝒓 which is π𝒓². The formula for the area of a circle is A = π𝒓².

Image caption, The formula for the area of a circle is used by multiplying π by the square of the radius. This can be entered on a calculator in different ways. π × 𝒓 × 𝒓, π × 𝒓² and 𝒓² × π. Each of these will give the same answer. Only the radius is squared.
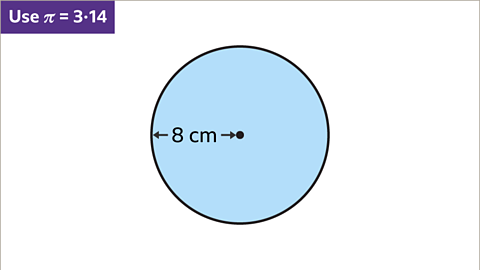
Image caption, Find the area of the circle to the nearest square centimetre. Use π = 3۰14

Image caption, The radius of the circle is 8 cm. Substitute 𝒓 = 8 into the formula for the area of the circle. Multiply π by the square of the radius. 3۰14 × 82 = 200۰96. The area of the circle is 201 cm to the nearest centimetre.
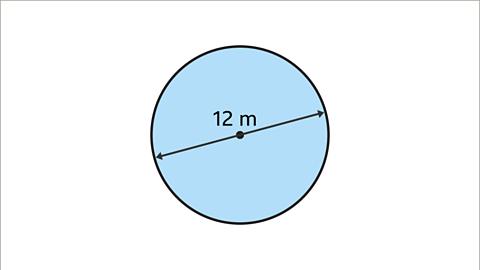
Image caption, Find the area of the circle. Use the π button on a calculator. Give the answer to 3 significant figures.

Image caption, The diameter of the circle is 12 m. The formula for the area of a circle uses the radius. The radius of the circle is half of the diameter. 12 ÷ 2 = 6. The radius of the circle is 6 cm.
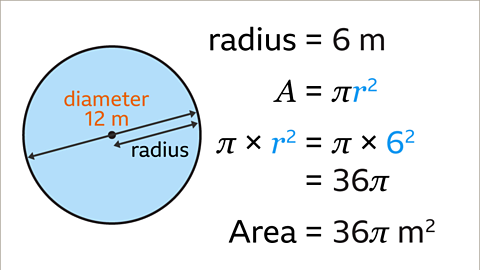
Image caption, Substitute 𝒓 = 6 into the formula for the area of the circle. Multiply π by the square of the radius. π × 62 = 36π. In terms of π, area of the circle is 36π m². This value needs to be given as a decimal and then rounded.
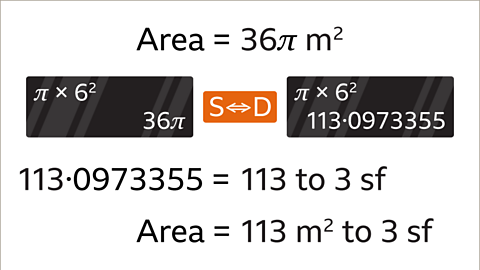
Image caption, The value 36π can be converted to a decimal by pressing the surd button on a scientific calculator. 36π as a decimal is 113۰0973355. This rounds to 113 to three significant figures. The area of the circle is 113 m² to three significant figures.
1 of 10
Question
Find the area of the circle, using π = 3۰142. Round the answer to three significant figures.
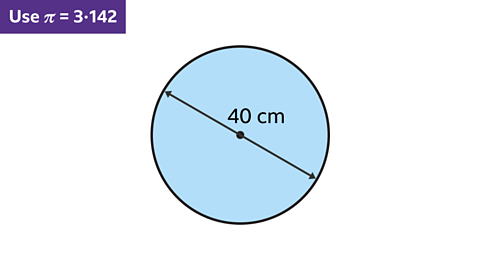
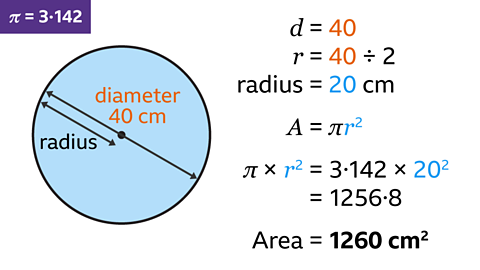
- The diameter of the circle is 40 cm.
- The formula for the area of a circle uses the radius.
- The radius of the circle is half of the diameter. 40 ÷ 2 = 20
The radius of the circle is 20 cm. - Substitute 𝒓 = 20 into the formula for the area of the circle.
- Multiply π by the square of the radius. 3۰142 × 20² =1256۰8
This must be rounded to three significant figures. - The area of the circle is 1260 cm² to three significant figures.
Calculating the radius and diameter of a circle, when given its area
The operations used to find the area are squaring the radius, then multiplying by π. The inverseWhen an operation is combined with its inverse, the number is unchanged. Multiplication and division are inverse operations. Eg, 3 × 10 ÷ 10 = 3 of multiply by π is divide by π. The inverse of square is square rootA square root of a number is a value that, when multiplied by itself, gives the number. Eg, 4 × 4 = 16, so the square root of 16 is 4.
To find the radius from the area of a circle, use the inverse operations:
Divide the area by π.
Find the square root.
To find the diameter, multiply the radius by 2
It may be useful to look at changing the subject.
Example

Image caption, To find the area of a circle, the radius is squared and multiplied by π. The inverse of this is to divide by π and find the square root.
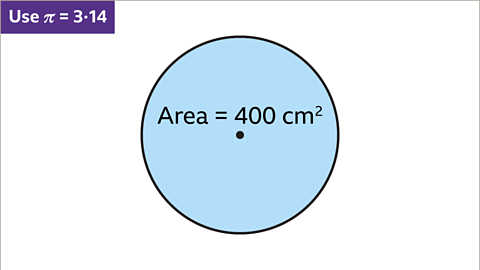
Image caption, Find the radius of a circle with area 400 cm². Use π = 3۰14. Give the answer to one decimal place.

Image caption, The formula to find the area of a circle is to square the radius and multiply by π. The inverse of this is divide the area by π, then square root. π𝒓² = 400. 3۰14 × r² = 400

Image caption, To find the radius, first divide by π. 400 ÷ 3۰14 = 127۰388535. Next, calculate the square root of the value. √(127∙388535)=11∙286655. This value needs to be rounded.

Image caption, 11∙286655 rounds to 11۰3 to one decimal place. The radius of the circle is 11۰3 cm to one decimal place.
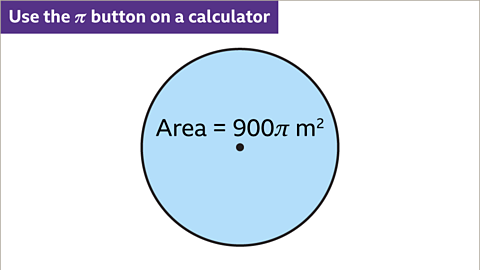
Image caption, Find the diameter of a circle with area 900π m².
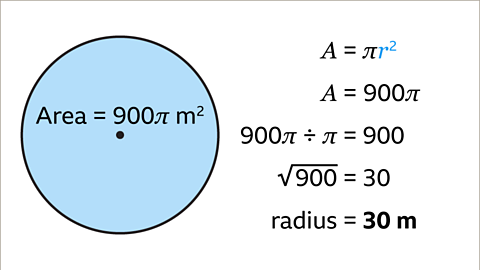
Image caption, The formula to find the area of a circle is to square the radius and multiply by π. The inverse of this is divide the area by π, then square root. 900π ÷ π = 900. The square root of 900 is 30. The radius of the circle is 30 m.
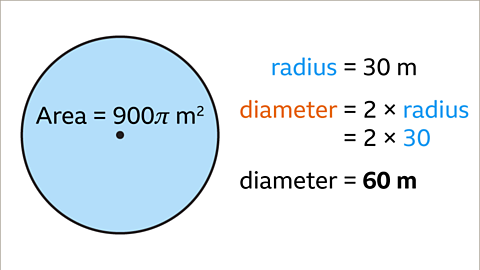
Image caption, The radius of the circle is 30 m. The diameter is twice the radius. 30 × 2 = 60. The diameter of the circle is 60 m.
1 of 8
Question
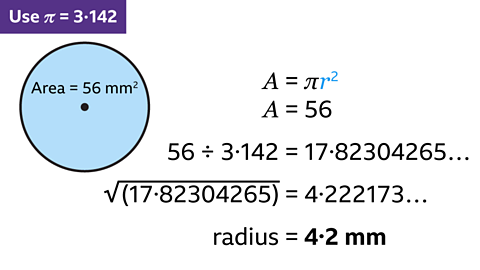
The circle has an area of 56 mm². Find the radius of the circle and give the answer to two decimal places.
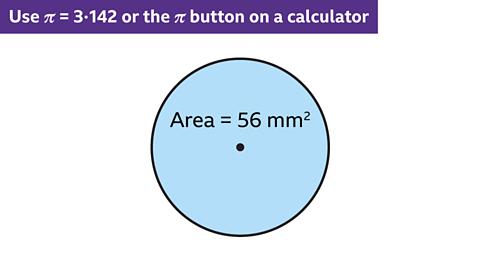
- The formula for the area of a circle squares the radius and multiplies by π. The inverse process is used to find the radius from the area.
Using π = 3۰142:
Divide the area of the circle by π. 56 ÷ 3۰142 = 17۰82304265
Square root the value then round to two decimal places
√17۰82304265 = 4∙221734554The radius of the circle is 4۰22 mm to two decimal places.
Using the π button on a calculator:
Divide the area of the circle by π. 56 ÷ π = 17۰82535363
Square root the value then round to two decimal places
√17۰82535363 = 4∙222008246The radius of the circle is 4۰22 mm to two decimal places.
Practise finding the area of a circle
Practise finding the area of a circle with this quiz. You may need a pen and paper to help you.
Quiz
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Perimeter, Area, Volume
Find out more by working through a topic
- count8 of 11
- count9 of 11
- count10 of 11
- count11 of 11