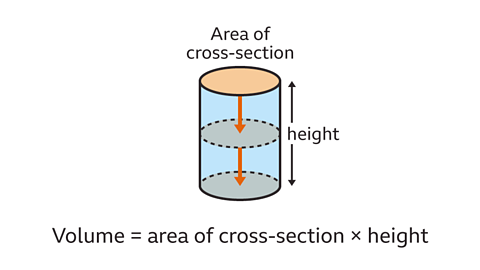
Key points
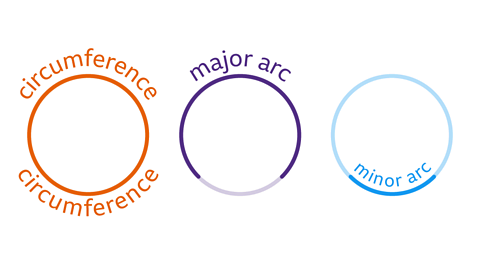
All circle calculations use the constant π (pi). The circumferenceThe distance around a circle; its perimeter. divided by the diameterThe distance across the circle, circumference to circumference, through its centre. gives π. This works for all circles because they are mathematically similar. The circumference is a length and is measured in units, including centimetres and metres.
Pi is an irrational numberA value that cannot be expressed exactly, such as √2 and π. An approximate value for pi is used in calculations; 3۰142 and 3۰14 are commonly used. A modern calculator uses the surdAn irrational number. This includes the square roots that cannot be written as an exact decimal and special values like π. notation of the symbol π which can be changed to a decimal approximation using the S
⇔
D key, which gives 3۰141592654The ability to round a number to a number of decimal places or to a number of significant figures means that answers can be written to an agreed degree of accuracy.

Video
Watch the video to learn how circles and circumference play an important role in the work Steph does as a football coach, and why circles play a useful part in sport generally.
Bobby: So, tell me about your role as a sports coach.
Steph: Yeah, so I’m mainly a football coach, I work with a brilliant group of under 14s girls, and I take their training sessions, manage them on match days, basically just make sure they get to play as much football as possible, enjoy it as much as possible and learn as much about the game as possible.
Bobby: So does the size of teams you manage vary?
Steph: This season, we’re playing eleven a side. Last season, we played nine, a couple of years ago we played seven, so as you go through the age groups, you progress from five a side, to seven, to nine, to eleven. And with that, the pitch size varies as well.
Bobby: How important is it to get the measurement of these pitches accurately done?
Steph: Yeah, so it’s really important. So, the main reason that we move through team sizes and pitch sizes as players get older is to match their development. So, how far might they be able to kick a ball, for example? How far might they be expected to run?
The other element is fairness, so in football, you’re not always playing on the same pitch. You might be playing on a training pitch, on a match pitch, at home, away. So obviously, to make sure that in a league, forexample, all of the games are fair, all of the games need to be played on the same size pitch.
Bobby: And how are these pitches actually measured then?
Steph: So, there is a groundskeeper that will do that. They will come and they will draw the lines on the grass. They use something called a measuring wheel and that wheel clicks every time it goes one metre, so the groundskeeper knows when they’ve got the right distance.
Bobby: Ah, and mathematically, the wheel that they use has to have a circumference of one metre? And to make sure that’s accurate, we can multiply the diameter, which goes through the centre of the wheel, by the ratio of pi which is about 3۰14, to give us one metre.
So, where else do we see circles in football and other sports?
Steph: Oh, all over. In football, you’ve got the centre circle where the whole game kicks off. You’ve even got the ball, so it’s really important again for fairness that the ball is the same size. And I know at elite levels, they’ll measure that, they’ll check that before a game kicks off.
It’s in other sports too, so cycling, for example, the wheels are circles. Then you’ve got Olympic sports, so things like hammer throw will start in a circle and people will have to spin themselves around in a circle.
Bobby: It just goes to show that circles and circumferences are so valuable throughout sport.
Steph: Oh, definitely.
Understanding the circle and π (pi)
To understand the circle, particular vocabulary must be learnt:
- The of a circle is its perimeterThe total distance around a shape..
- An arcPart of the circumference. Named as major for over half of the circumference and minor for less than half of the circumference. is part of the circumference.
- The diameterThe distance across the circle, circumference to circumference, through its centre. is the whole distance across the circle through its centre.
- The radiusThe distance from the centre of the circle to the circumference. is the distance from the circumference to the centre of the circle.
- The radius is half the diameter.
What is π (Pi)?
- π (pi)Pi is used to represent the ratio of a circumference of a circle to its diameter, denoted with the Greek symbol π is the ratio of the circumference of a circle to the length of its diameter.
- For all circles, the circumference divided by the diameter gives π.
- Pi (π) is a constant.
- π is an irrational numberA value that cannot be expressed exactly, such as √2 and π, it cannot be expressed exactly so approximations are used in calculations. π is rounded most often to 3۰142 or 3۰14. The π button on a calculator gives greater accuracy.
- When using the π button the answer may be given in terms of π. The surd display can be changed to a decimal value by pressing the S
⇔
D button. - The final answer is rounded to the degree of accuracy asked for in the question. This may be a specific number of decimal places or significant figures.
Example

Image caption, The vocabulary of the circle includes the terms circumference, arc, diameter, and radius.
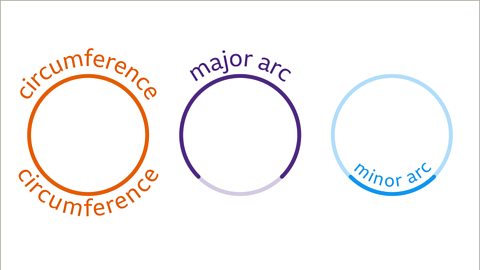
Image caption, The circumference of a circle is the distance around the shape. The circumference is the perimeter of the circle. An arc is a part of the circumference. A major arc is greater than half the total circumference, a minor arc is less than half the circumference.
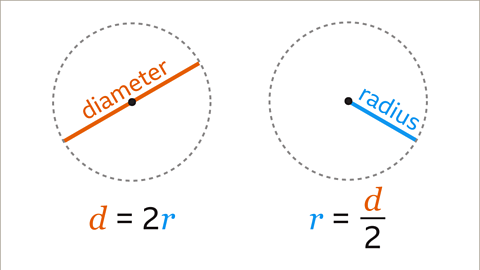
Image caption, The diameter is the whole distance across the circle, through its centre. The diameter is two radii. The radius is half of the diameter. The radius is the distance from the centre of the circle to the circumference, or the distance from the circumference of the circle to its centre. No matter where the diameter and radius are measured, they will have a fixed value for a given circle.
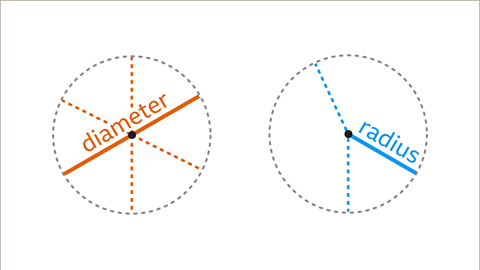
Image caption, No matter where the diameter and radius are measured, they are a fixed size for a given circle.

Image caption, π (pi) is a constant used in circle calculations.
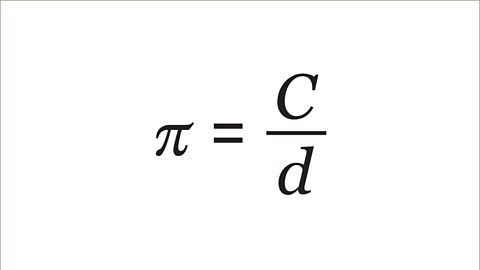
Image caption, π is the ratio of the circumference of a circle and its diameter. The circumference divided by the diameter is π.

Image caption, In calculations the π button on the calculator gives 3۰141592654. Frequently used approximations include 3۰142 and 3۰14
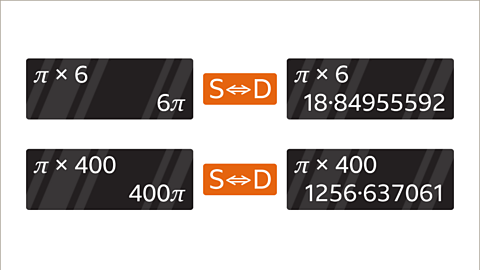
Image caption, When using the π button on a calculator the display may use surd notation and give the answer in terms of π. This can be changed to a decimal value by pressing the S<=>D button, which changes surd notation to a decimal value. When doing this π × 6 = 6π becomes 18۰84955592 and π × 400 = 400π becomes 1256۰637061

Image caption, The final answer is rounded to the degree of accuracy asked for in a question. This may be a given number of decimal places (dp) or significant figures (sf). For example, 18۰844955592 rounded to two decimal places is 18۰85 and 1256۰637061 rounded to three significant figures is 1260
1 of 9
Question
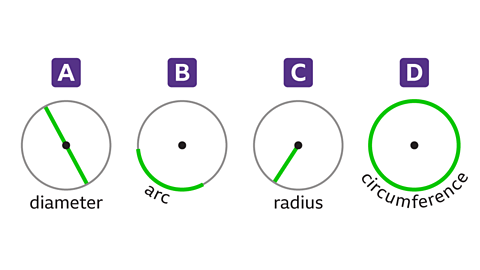
Name the highlighted part of each circle.
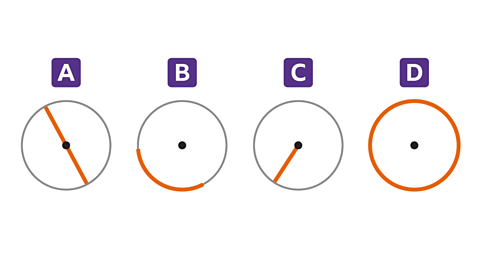
A shows the diameter. This is the distance across the circle, through its centre.
B shows an arc. This is part of the circumference. It is a minor arc as it is less than halfway around the circle.
C is a radius. This is the distance from the centre of the circle to the circumference.
D shows the circumference. This is the perimeter of the circle, the distance around the shape.
Calculate the circumference of a circle
To find the of a circle use the given approximation for π or the π button on a calculator and either the diameterThe distance across the circle, circumference to circumference, through its centre. or the radiusThe distance from the centre of the circle to the circumference..
- The formula for the circumference when using the diameter is 𝑪 = π𝒅
- Substitute the value of the diameter into the formulaA fact, rule, or principle that is expressed in words or in mathematical symbols. Plural: formulae..
- Multiply π by the diameter of the circle.
- The formula for the circumference when using the radius is 𝑪 = 2π𝒓
- Substitute the value of the radius into the formula.
- Multiply 2 by π then multiply by the radius, or multiply π by double the radius. (Double the radius is the same as the diameter).
- Round the answer to the degree of accuracy asked for in the question. This may involve rounding to a number of decimal places, dp, or rounding to a number of significant figures, sf.
To find the circumference in terms of π.
- When the π button is used on a calculator the answer is automatically given in terms of π. Working without a calculator, the circumference is the diameter value written before π.
Examples
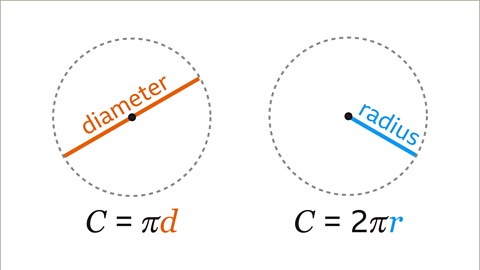
Image caption, The formula for the circumference of a circle uses either the diameter or the radius of the circle.
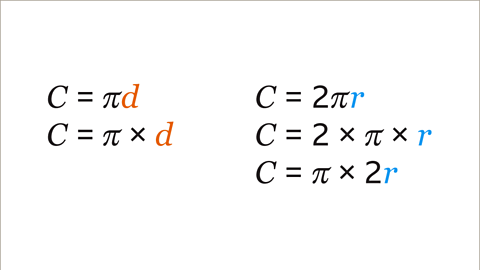
Image caption, The formula using the diameter is 𝑪 = π𝒅. Multiply π by the diameter of the circle. The formula using the radius is 𝑪 = 2π𝒓. This means that 2 is multiplied by π and then multiplied by the radius. This may be worked out without a calculator. Multiply π by double the radius. When using a calculator, the numbers are entered in the order of the formula.
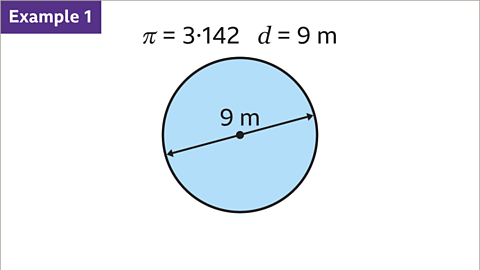
Image caption, Using π = 3۰142, find the circumference a circle with a diameter of 9 m. Give the answer to 2 decimal places.
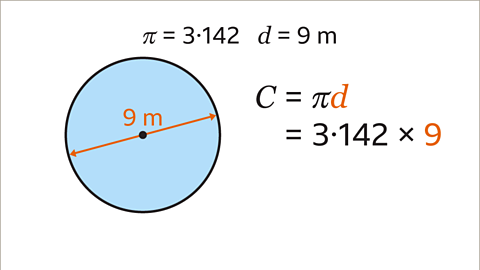
Image caption, The formula for the circumference using the diameter is 𝑪 = π𝒅. Substitute the value of the diameter into the formula. Multiply π by the diameter of the circle. 3۰142 × 9

Image caption, 3۰142 × 9 = 28۰278. This is rounded to 2 decimal places. The circumference of the circle is 28۰28 m to 2 dp.
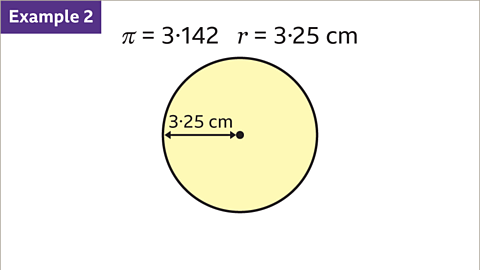
Image caption, Using π = 3۰142, find the circumference a circle with a radius of 3۰25 cm. Give the answer to 3 significant figures.
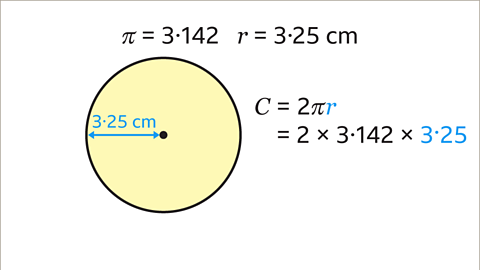
Image caption, The formula for the circumference, using the radius, is 𝑪 = 2π𝒓. Substitute the value of the radius into the formula. Multiply 2 by π then multiply by the radius. 2 × 3۰142 × 3۰25
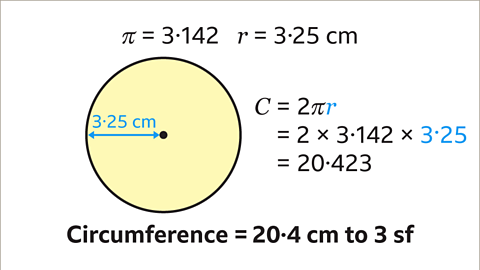
Image caption, 2 × 3۰142 × 3۰25 = 20۰423. This is rounded to 3 significant figures. The circumference of the circle is 20۰4 cm to 3 sf.
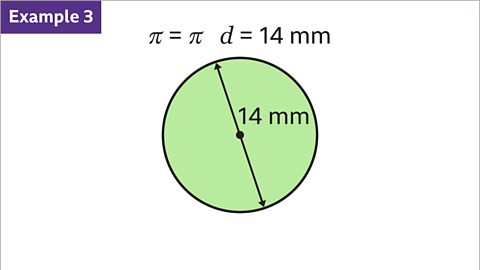
Image caption, Find the circumference a circle with a diameter of 14 mm. Give the answer in terms of π.
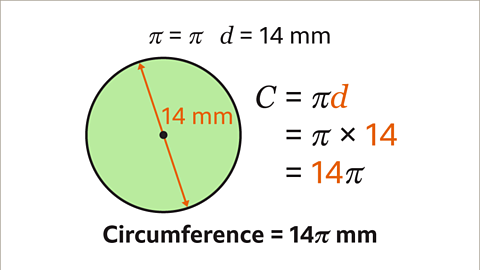
Image caption, The formula for the circumference using the diameter is 𝑪 = π𝒅. Substitute the value of the diameter into the formula. Multiply π by the diameter of the circle. π × 14 = 14π. The circumference of the circle is 14π mm.
1 of 10
Question
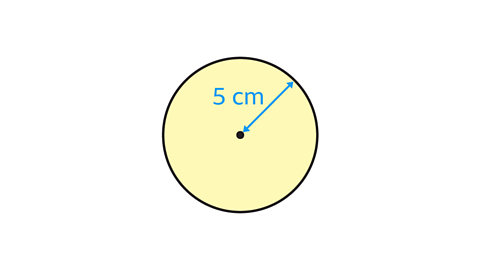
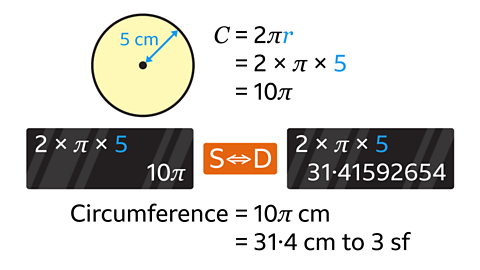
What is the circumference of a circle with a radius of 5 cm? Give the answer in terms of π and to 3 significant figures.
The formula for the circumference of a circle is 𝑪 = 2π𝒓.
Substitute the value of the radius into the formula and calculate.
2 × π × 5 = 10π
2 × π × 5 = 31۰41592654
The circumference of the circle is 10π cm which is31۰4 cm to 3 sf.
Calculate the diameter or radius of a circle, given its circumference
To work out the diameter and the radius of a circle from its circumference.
- Divide the circumference by π. This gives the diameter.
- The radius is half of the diameter.
Examples
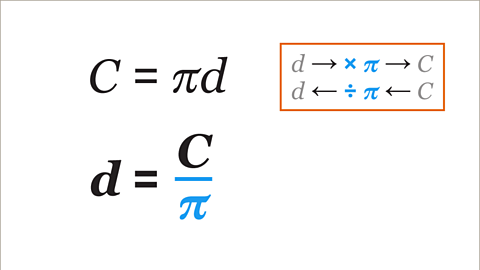
Image caption, The circumference of a circle is given by the formula 𝑪 = π𝒅. The diameter has been multiplied by π to give the circumference. The inverse of multiply by π is divide by π. The circumference divided by π gives the diameter.
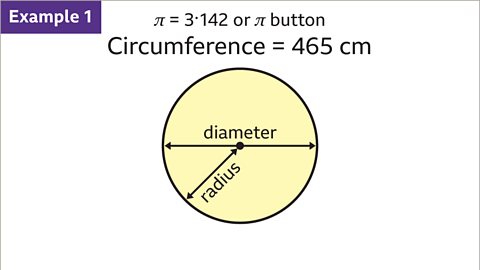
Image caption, Find the diameter and the radius of a circle with a circumference of 465 cm. Give the answer to the nearest centimetre. Use π = 3۰142 or the π button on a calculator.
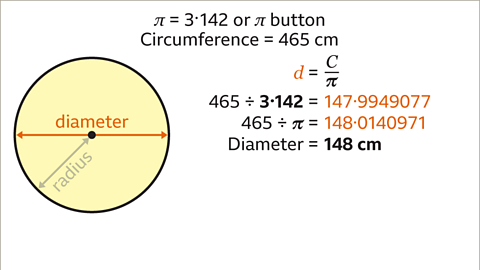
Image caption, Divide the circumference by π. Using the π button it would be 465 ÷ 3۰142 = 147۰9949077. 465 ÷ π =148۰0140971. The diameter of the circle is 148 cm to the nearest cm.
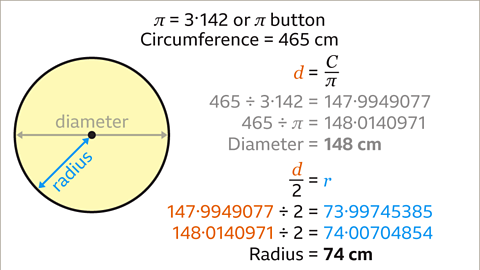
Image caption, The radius is half of the diameter. 147۰994907 ÷ 2 =73۰99745385. 148۰0140971 ÷ 2 =74۰00704854. The radius of the circle is 74 cm to the nearest cm.
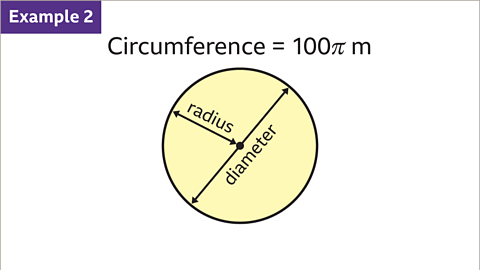
Image caption, The circumference of a circle is 100π m. Find the diameter and the radius of the circle.
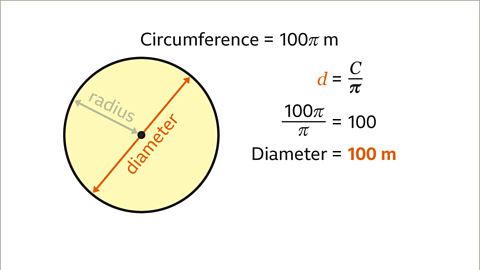
Image caption, Divide the circumference by π. 100 π ÷ π = 100. The diameter is 100 m.
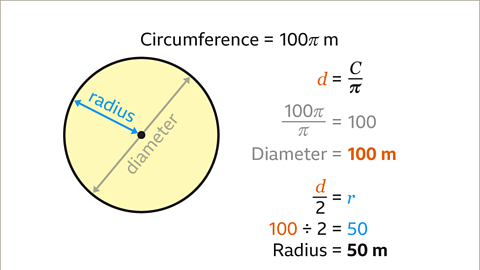
Image caption, The radius is half of the diameter. 100 ÷ 2 = 50. The radius of the circle is 50 m.
1 of 7
Practise pi and working out circumference
Practise pi and working out the circumference of circles with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

The age of a tree can be found by counting the concentricCircles in a plane that have the same centre rings in the cross-section of the trunk. In practical terms, chopping down a tree is not environmentally sound, so another method has been developed using the circumference of a tree trunk.
Measuring the circumference at a height of 1۰4 m (about 4’ 6”) and dividing by π gives the diameter of the tree. Multiplying the diameter by the growth factor for the particular species of tree then gives an estimate for the tree’s age.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Perimeter, Area, Volume
Find out more by working through a topic
- count7 of 11
- count8 of 11
- count9 of 11
- count10 of 11