Surface area and volume of a cylinder - KS3 Maths

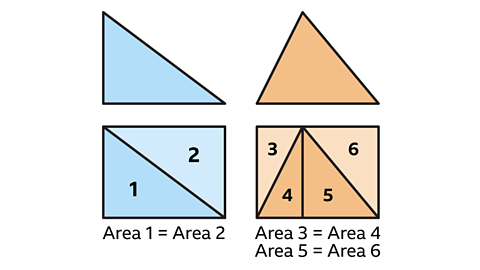
Key points

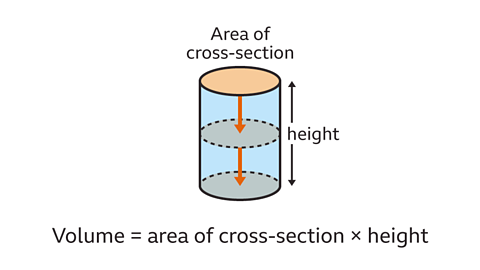
An image of an upright cylinder. Drawn right: an arrow to represent the height of the cylinder. The arrow is labelled as height. The top circular face of the cylinder is coloured orange and labelled: area of cross section. Two further circles through the shape, one being the base, have been coloured orange. The edges of these circles are drawn with a dashed curve. Downward orange arrows to illustrate the uniform cross section are drawn between the circles. Written below, the formula: volume equals area of cross section multiplied by height. The cylinder is coloured blue. — Image caption,
The volume of a cylinder is the area of the cross-section multiplied by the height.

A good understanding of calculations for the circumference of a circle and the area of a circle is useful when calculating the surface area and volume of a .

A cylinder is a shape with a circular .
The total of a cylinder is made up of two circular and a curved surface which makes a rectangle if flattened out. Surface area is measured in square units, such as cm² and m².
The of a cylinder is the of its cross-section, a circle, multiplied by its height. Volume is measured in cubic units, such as cm³ or m³.

Calculate the area of a cylinder

A cylinder is made up of two circles that are directly opposite one another, and a rectangle.
Calculations may be carried out numerically using a decimal approximation for (pi), such as 3۰14 or 3۰142. Workings may also be written symbolically in terms of π. This means that the result is given as a multiple of π.
On a scientific calculator, the S
⇔
D button is used to convert a value in terms of π to a decimal value.

To calculate the surface area of a cylinder:

Work out the area of the two circular faces (2 × π\(r\)²).
Work out the curved surface area, this is the rectangular face (2π\(r\) × \(h\)).
Sum the area of the circles and the rectangle.

The expression for working out the total surface area of a cylinder is
2π\(r\)² + 2π\(rh\).

\(r\) is the radius of the circular cross-section and \(h\) is the height of the cylinder.
If the diameter, \(d\), of the circular cross-section is given, this is halved to find the radius.

Depending on the orientation of the cylinder, the length of the cylinder is its height.

Example

Skip image gallery

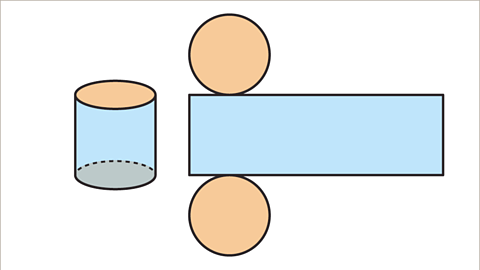
Image caption,
A cylinder is made up of two congruent circles and a rectangle. The circles are the top face and the base face of the cylinder. The circles are directly opposite each other. The rectangle is the curved face around the cylinder.
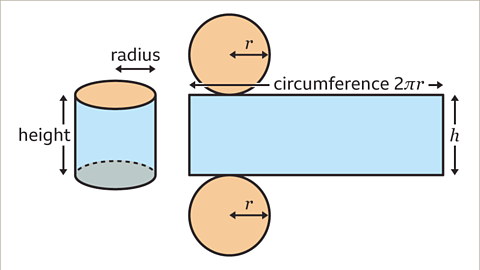
Image caption,
To work out the surface area, the radius and the height of the cylinder are used. Each circle has the radius, 𝒓. The rectangle’s length is the circumference of the circular cross-section, this is 2π𝒓 or π𝒅. The width of the rectangle is the height of the cylinder, 𝒉.
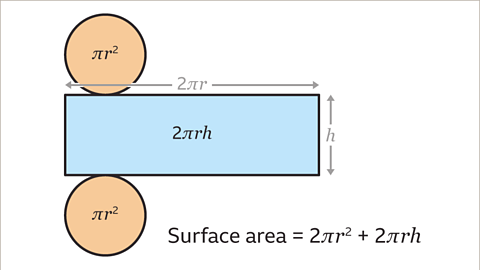
Image caption,
The total surface area of the cylinder is two circle areas, 2 × π𝒓², plus the curved surface area of the rectangle, 2π𝒓 × 𝒉. This gives the formula, surface area = 2π𝒓² + 2π𝒓𝒉.
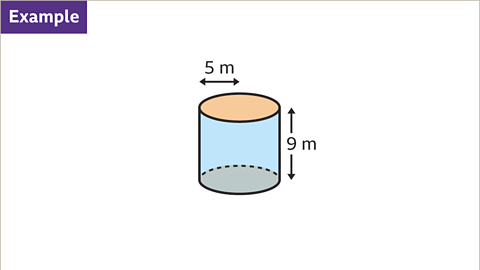
Image caption,
Work out the surface area of the cylinder. Use π = 3۰142 or the π button on a calculator. Give the answer to 3 significant figures.
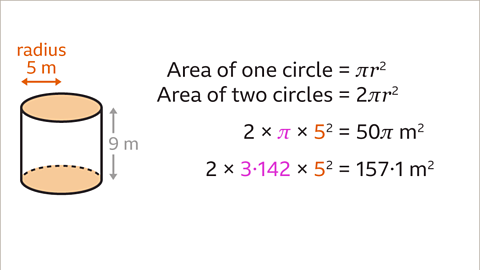
Image caption,
The radius of the circular cross-section is 5 m. The area of one circular face is πr². When using the π button on the calculator, the area of both circular faces is 2 × π × 5² = 50π m². When using the approximation π = 3۰142, the area of both circular faces is 2 × 3۰142 × 5² = 157۰1 m².
Image caption,
The area of the curved surface (the rectangle) is 2πr × 𝒉. The radius is 5 m and the height is 9 m. When using the π button, the area of the curved rectangular face is 2 × π × 5 × 9 = 90π m². When using the approximation π = 3۰142, the area is 2 × 3۰142 × 5 × 9 = 282۰78 m².
Image caption,
Sum the areas of the circles and the rectangle. 50π + 90π = 140π. When using the π button, the total surface area of the cylinder is 140π m². When using the approximation π = 3۰142, the total surface area is 157۰1 + 282۰78 = 439۰88 m².
Image caption,
The answer 140π can also be given as a decimal using the S⇔D button on a calculator. This button is used to convert a value in terms of π to a decimal value. This gives 439۰8229715, which rounds to 440 m² to 3 significant figures.
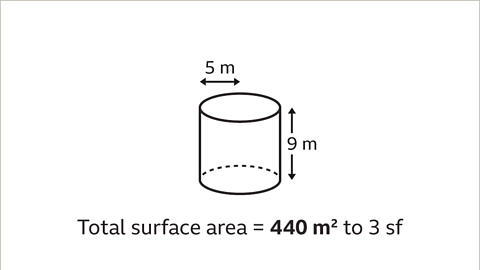
Image caption,
The total surface area of the cylinder is 440 m² to 3 significant figures.

Question

Use the formula to work out the surface area of the cylinder.

Use the approximation π = 3۰14. Give your answer to the nearest mm².

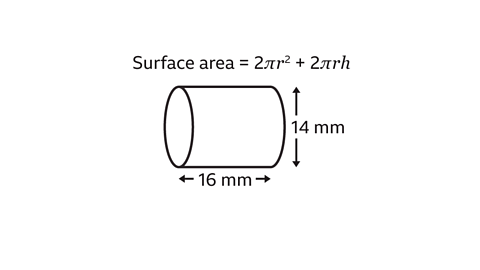
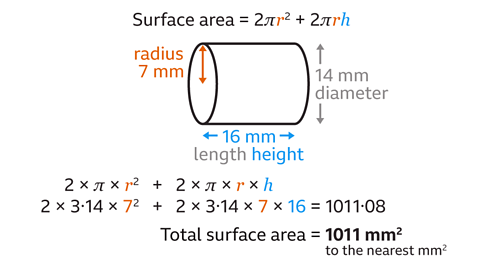
An image of a horizontal cylinder. The length of the cylinder is labelled as sixteen millimetres. The diameter of the circular face is labelled as fourteen millimetres. Written above, the formula: surface area equals two pi r squared plus two pi r h.

Calculate the volume of a cylinder

The volume of any cylinder is the area of the cross-section multiplied by its height.
This is given by the formula \(V\) = π\(r\)²\(h\) , where \(r\) is the radius of the circular cross-section and \(h\) is the height of the cylinder.

To work out the volume of a cylinder:

Find the area of the cross-section using the formula for the area of a circle, \(A\) = π\(r\)².
Multiply by the height of the cylinder.

Examples

Skip image gallery

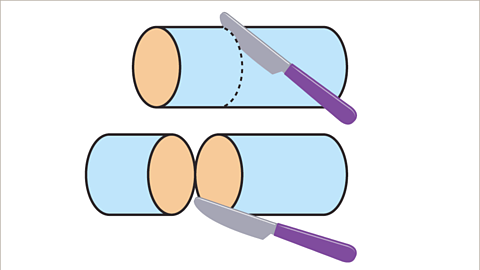
Image caption,
Imagine that a solid cylinder is sliced open. The face that is revealed is called the cross-section. The cross-section of a cylinder is a circle. The cross-section is the same all the way through the cylinder.
Image caption,
The volume of a cylinder is the area of the cross-section multiplied by the height (or length) of the cylinder.
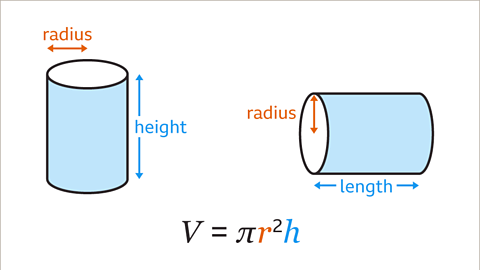
Image caption,
The formula for the volume of a cylinder uses height. Length can be used in place of height as they are the same dimension.
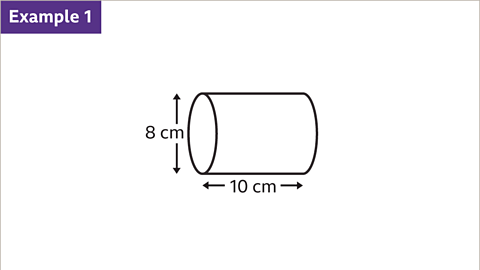
Image caption,
Work out the volume of the cylinder, giving the answer to the nearest whole number. Use the π button on a calculator or the approximation π = 3۰142
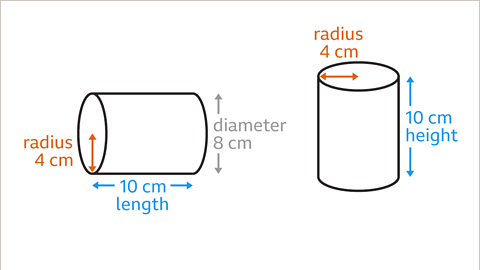
Image caption,
The diameter of the circular cross-section is 8 cm. The radius is half of the diameter. The radius, 𝒓, is 4 cm. The length of the cylinder is 10 cm. The length can also be described as the height, 𝒉, of the cylinder.
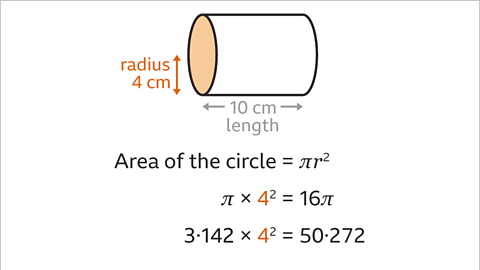
Image caption,
Firstly, work out the area of the cross-section of the cylinder (a circle). Using π on a calculator, the area of the cross-section is π × 4² = 16π. Using the approximation π = 3۰142, the area of the cross-section is 3۰142 × 4² = 50۰272
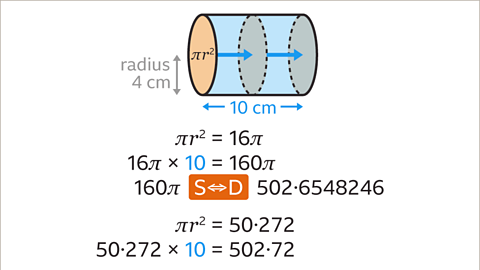
Image caption,
Now multiply the area of the circle by the length of the cylinder. 16π × 10 = 160π. Using the S⇔D calculator button, this is 502۰6548246. Using the approximation π = 3۰142, the calculation is 50۰272 × 10 = 502۰72. This value now needs to be rounded.
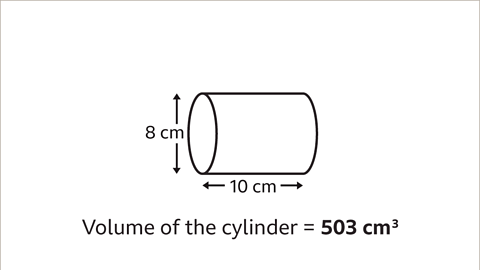
Image caption,
Round to the nearest whole number. Both 502۰6548246 and 502۰72 round to 503. The volume of the cylinder is 503 cm³.
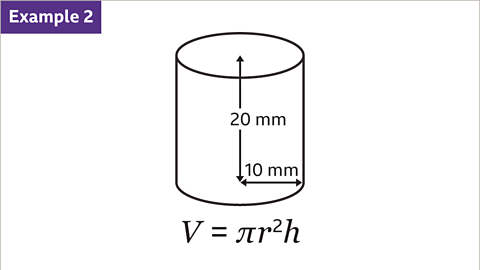
Image caption,
Use the formula to find the volume of the cylinder. Use the approximation π = 3۰142
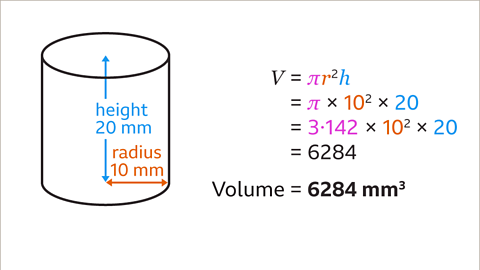
Image caption,
Substitute the value of the radius, 𝒓 = 10, and the height, 𝒉 = 20, into the formula 𝑽 = π𝒓²𝒉, and work out the calculation. 3۰142 × 10² × 20 = 6284. The volume of the cylinder is 6284 mm³.

Question

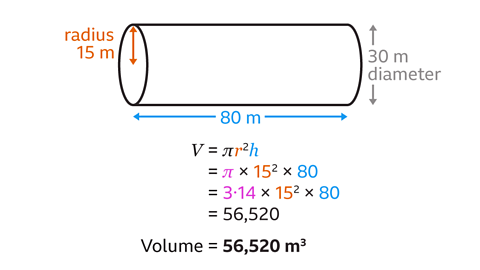
What is the volume of the cylinder? Use the approximation π = 3۰14

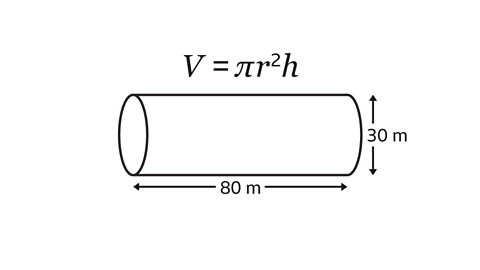
An image of a horizontal cylinder. The length of the cylinder is labelled as eighty metres. The diameter of the circular face is labelled as thirty metres. Written above: v equals pi r squared h.

Practise finding the surface area and volume of cylinders

Practise working out the surface area and volume of cylinders with this quiz. You may need a pen and paper to help you with your answers.

Quiz

Real-life maths

An image of tinned food. Each tin is a cylinder. Some of the lids have been partially removed to show their contents. — Image caption,
Certain foods are commonly sold in cylinder-shaped tins.

Certain foods, such as baked beans, vegetables, fish and meat, are commonly sold in cylinder-shaped tins. Cylinders pack efficiently into boxes for shipping, taking up approximately 90% of the available space.

Their circular cross-section also means that the tins can withstand pressure when stored. The food contained in them has a long shelf life.

To make the tins accurately, manufacturers need to calculate the surface area plus a small amount of extra area for the seams. The volume of the cylinder shape will determine the quantity of food that can go inside a tin.