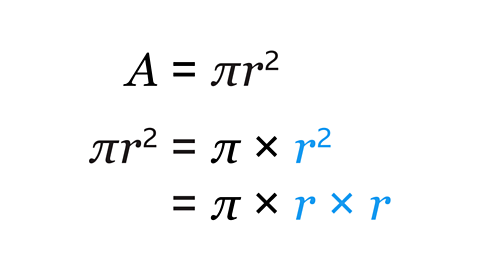Key points
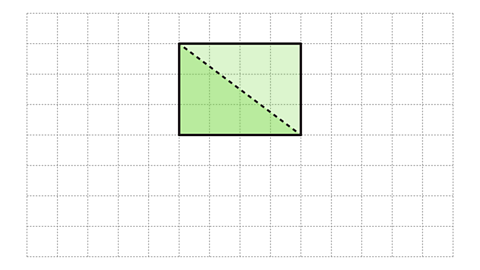
Any triangleA three-sided polygon. can be shown to be half of a rectangleA quadrilateral with opposite pairs of sides that are both equal in length and parallel. All four angles are right angles.. This can be shown in diagrams and practically using paper and scissors.
The areaA measure of the size of any plane surface or 2D shape. Area is measured in square units, for example, square centimetres or square metres: cm² or m². of a triangle is calculated by finding the length of the base, halving it, and then multiplying it by the perpendicularPerpendicular lines are at 90° (right angles) to each other. height. Alternatively, multiply the base length by the perpendicular height and then halve to find the area of a triangle.
The base and the perpendicular height are at right angles to each other. The measurements used must be in the same units. For example, to work in cm a 45 mm measurement would have to be converted to 4۰5 cm. Practising converting metric units will help with this process.

Understanding the formula for the area of a triangle
The area of a triangle is calculated by the formulaA fact, rule, or principle that is expressed in words or in mathematical symbols. Plural: formulae.: \( \frac{1}{2} \) × base × perpendicular height.
- A rectangle can be divided into two congruentShapes that are the same shape and size, they are identical. triangles.
- The length and width of the rectangle are the base and height of a triangle. The base and the height are at right-angles, making the height the perpendicular height.
- For a right-angled triangle, the base and the perpendicular height are interchangeable.
- The orientationThe position of a shape in relation to a coordinate system. Orientation is the way an object is angled. of the triangle means that the base is not necessarily horizontal.
- For triangles that are not right-angled, the base is one of the sides and the perpendicular height may be shown either inside or outside the shape, it is not another side.
- The base is one side of the triangle. The perpendicular height is the perpendicular measurement that gives the other dimension of the triangle.
The formula can be presented as:
𝑨 = \( \frac{𝒃𝒉}{2} \)or 𝑨 = \( \frac{1}{2} \) 𝒃𝒉
- 𝑨 is the area of the triangle.
- 𝒃 is the length of the base of the triangle.
- 𝒉 is the length of the perpendicular height of the triangle.
Example
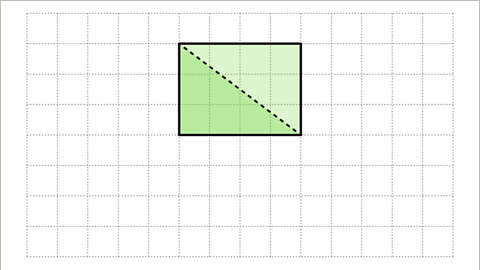
Image caption, The rectangle has been cut into two congruent triangles by drawing a diagonal.
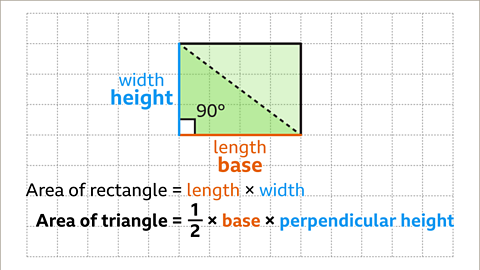
Image caption, The triangles are identical. The area of one triangle is equivalent to half of the area of the rectangle. The area of the rectangle is the length multiplied by the width. The length and width of the rectangle are the base and perpendicular height of the triangle, they are at right-angles to each other. The area of the triangle is half of the base multiplied by the perpendicular height.
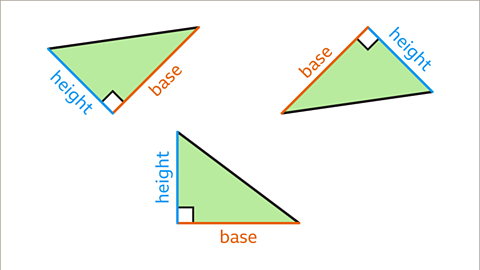
Image caption, For a right-angled triangle, the base and the perpendicular height are the two sides that are at right angles. The perpendicular height is the perpendicular measurement that gives the other dimension of the triangle. The terms are interchangeable and each of the perpendicular sides can be the base or the height. The orientation of the triangle means that the base is not necessarily horizontal or the lowest side of the shape.
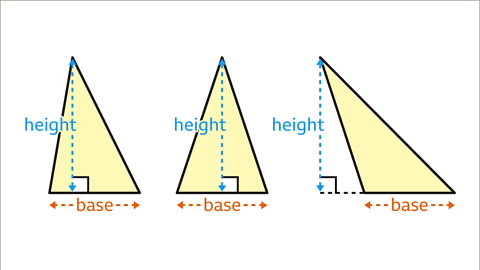
Image caption, For triangles that are not right-angled, the base is one of the sides and the perpendicular height may be shown either inside or outside the shape, it is not another side.
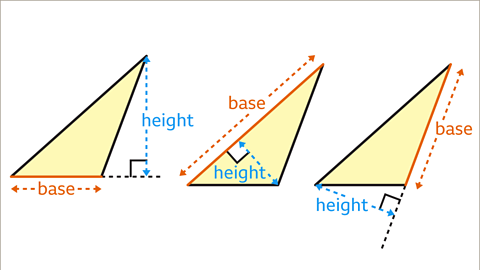
Image caption, The base is one side of the triangle. The perpendicular height is the perpendicular measurement that gives the other dimension of the triangle.
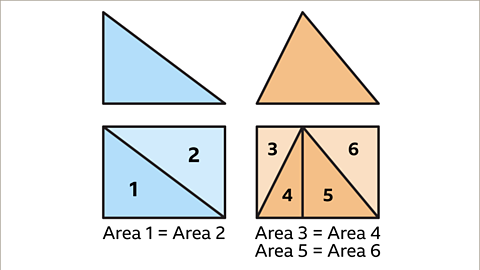
Image caption, A triangle is half of a rectangle. This can be shown in a diagram.
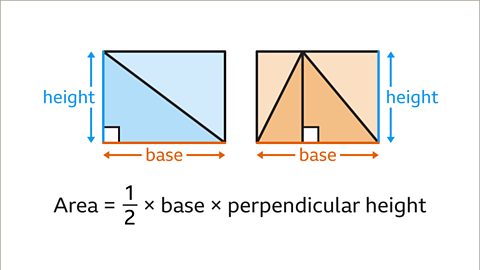
Image caption, The area of one triangle is ½ × base × perpendicular height.
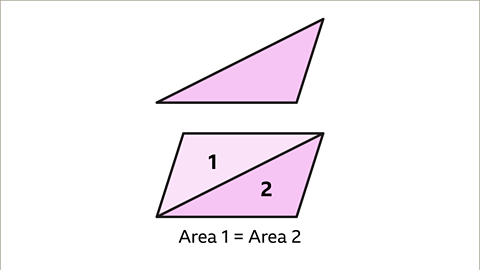
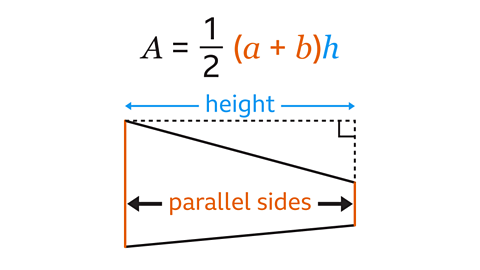
Image caption, It is not always clear straightaway that a triangle is half of a rectangle. Two identical triangles make a parallelogram, a quadrilateral with opposite pairs of sides that are both equal in length and parallel (always equal distances from each other). The two triangles have the same area, half of the parallelogram.
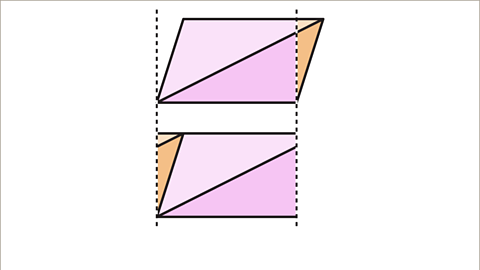
Image caption, The parallelogram can be cut to make a rectangle. The rectangle is made up of the two original triangles. Each triangle is half the area of the rectangle.
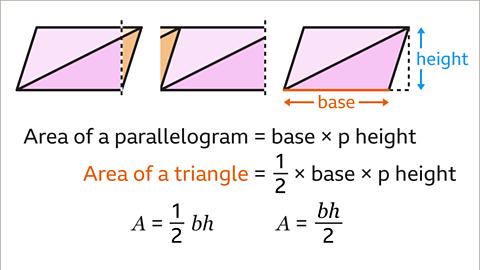
Image caption, The area of a parallelogram is base × perpendicular height. The area of one triangle is half of the parallelogram, this is ½ × base × perpendicular height. The formula can be written in equivalent forms, 𝑨 = ½ 𝒃𝒉 and 𝑨 = ᵇʰ⁄₂.
1 of 10
Question
Which lettered lengths can be used as the base and perpendicular height for the given triangles?
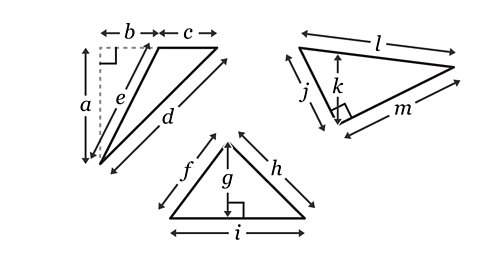
The base and the perpendicular height of the triangle must be at right-angles.
The base and heights for the triangles are:
𝒄 and 𝒂
𝒄 is one side of the triangle and 𝒂 is the height of the triangle, perpendicular to 𝒄.
𝒊 and 𝒈
𝒊 is one side of the triangle and 𝒈 is the height of the triangle, perpendicular to 𝒊.
𝒎 and 𝒋
They are two sides of the triangle and are at right-angles. Either of the sides can be used as the base and perpendicular height.
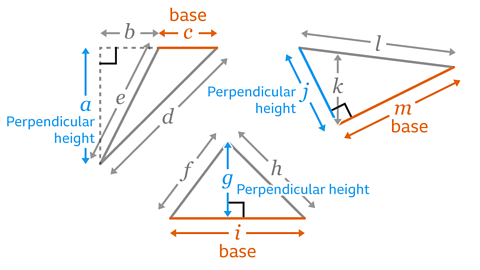
Calculating the area from the base and perpendicular height
The area of a triangle is \( \frac{1}{2} \) × base × perpendicular height. Multiplication is commutativeAn operation is commutative if the order does not matter. Multiplication and addition are commutative, eg 4 × 3 = 3 × 4 and 4 + 3 = 3 + 4 so the calculation can be processed in different orders.
The formula can be presented as:
𝑨 = \( \frac{𝒃𝒉}{2} \)or 𝑨 = \( \frac{1}{2} \) 𝒃𝒉
- 𝑨 is the area of the triangle.
- 𝒃 is the length of the base of the triangle.
- 𝒉 is the length of the perpendicular height of the triangle.
To work out the area of a triangle:
- Identify the base and the perpendicular height of the triangle. They must be measured in the same units.
- Substitute the base and height into the formula.
- Perform the calculation in one of three ways, all of which will give the same answer:
- Multiply the base by the perpendicular height, then divide by two.
- Find half of the base, then multiply by the perpendicular height.
- Find half of the perpendicular height, then multiply by the base.
Examples
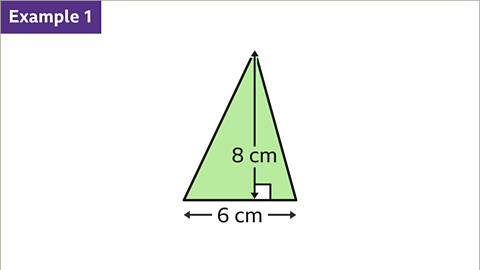
Image caption, Find the area of the triangle.
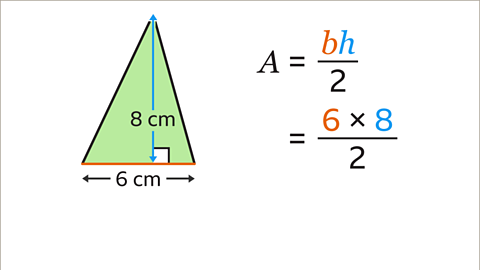
Image caption, The base and the perpendicular height of the triangle are in the same units. The base of the triangle is 6 cm. The perpendicular height is 8 cm. Substitute the values of the base and the perpendicular height into the formula. 𝒃 = 6 and 𝒉 = 8
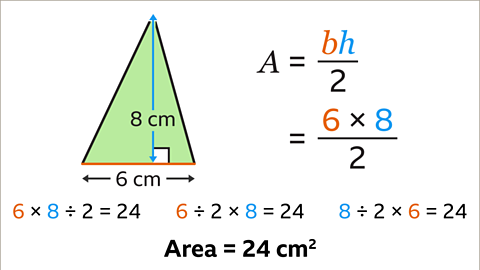
Image caption, The calculation (6 × 8) ÷ 2 can be worked out in three different ways. Each method gives the same answer of 24. Therefore, the area of the triangle is 24 cm².
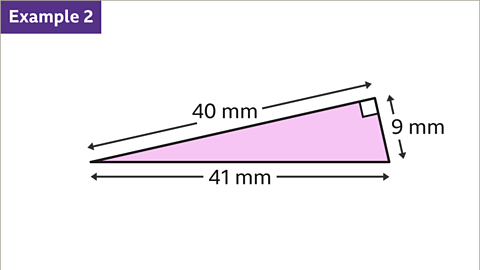
Image caption, Find the area of this right-angled triangle.
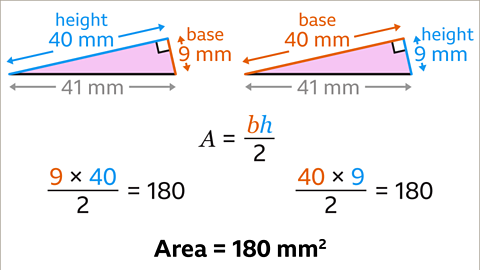
Image caption, All three side measurements are given. The longest side of 41 mm is not used because it is not at right angles to either of the other two sides. The sides that are at right angles are 9 mm and 40 mm. One of these is the base and the other is the perpendicular height. If the base is 9 mm the perpendicular height is 40 mm. If the base is 40 mm the perpendicular height is 9 mm. The calculations (9 × 40) ÷ 2 and (40 × 9) ÷ 2 give the same answer. The area of the triangle is therefore 180 mm²
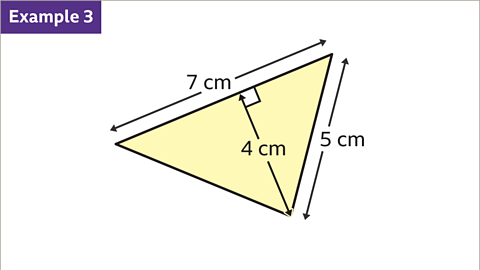
Image caption, Work out the area of the triangle.
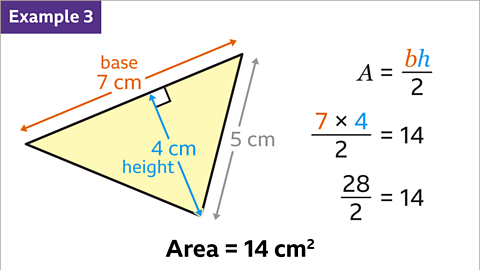
Image caption, All the measurements are in the same units. The base and the perpendicular height are at right angles. The base is 7 cm. The perpendicular height is 4 cm. Substitute the base and perpendicular height values into the formula. (7 × 4) ÷ 2 = 28 ÷ 2 = 14. The area of the triangle is therefore 14 cm²
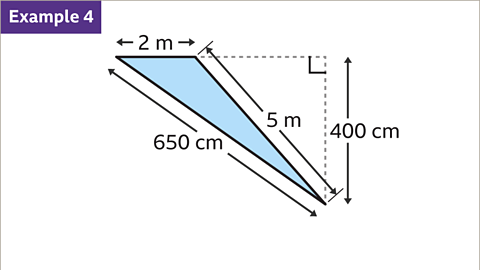
Image caption, Work out the area of the triangle.
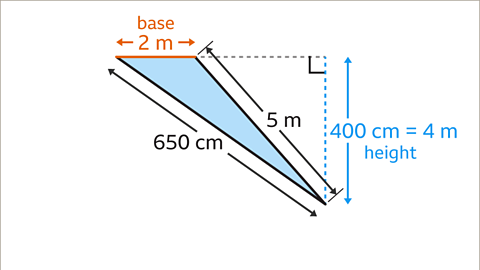
Image caption, The measurements are not in the same units. The base and the height are at right angles. The base is 2 metres. The height is 400 cm. Convert the units to match, so 400 cm = 4 m
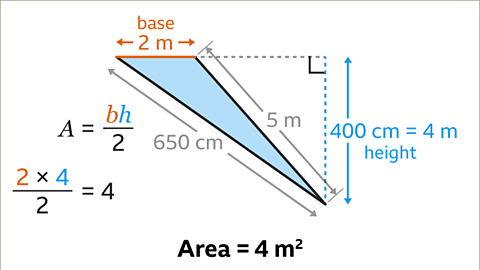
Image caption, The base and the height are at right angles. The base is 2 m. The height is 4 m. Substitute the base and perpendicular height values into the formula. (2 × 4) ÷ 2 = 4 and (8 ÷ 2) = 4. The area of the triangle is 4 m²
1 of 10
Question
Work out the area of the triangle.

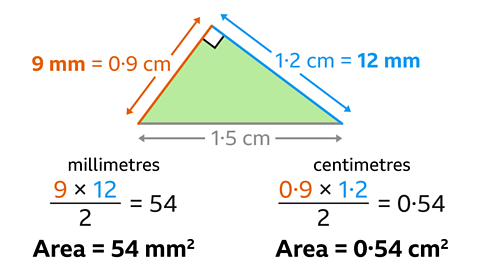
The base is 9 mm and the perpendicular height is 1.2 cm. They are not in the same units.
Working in millimetres, the base is 9 mm and the perpendicular height is 12 mm. Substitute the base and height values into the formula. (9 × 12) ÷ 2 = 54
- The area of the triangle is 54 mm²
Working in centimetres the base is 0∙9 cm, and the height is 1.2 cm. Substitute the base and height values into the formula.
(0∙9 × 1.2) ÷ 2 = 0∙54- The area of the triangle is 0∙54 cm²
The base and the perpendicular height are interchangeable. For a base of 12 mm and a perpendicular height of 9 mm, the answer is the same.
(12 × 9) ÷ 2 = 54
Calculating the base or perpendicular height from the area
- To calculate the base of a triangle, choose one of two methods. Both calculations give the same answer.
Method 1: Multiply the area of the triangle by two, then divide by the perpendicular height.
Method 2: Divide the area of the triangle by the perpendicular height, then multiply by two.
- To calculate the perpendicular height of a triangle, choose one of two methods. Both calculations give the same answer.
Method 1: Multiply the area of the triangle by two, then divide by the base.
Method 2: Divide the area of the triangle by the base, then multiply by two.
Examples
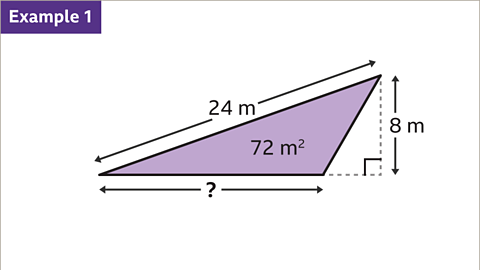
Image caption, The triangle has an area of 72 m². Find the base of the triangle.
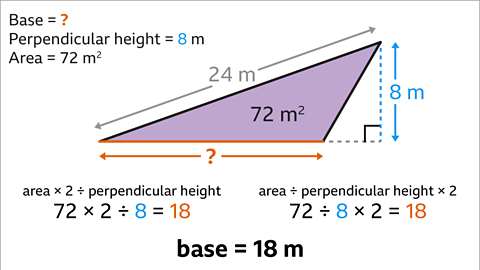
Image caption, The height of the triangle is perpendicular to the base. The perpendicular height is 8 m. Use one of two calculations to work out the base. Multiply the area of the triangle by two, then divide by the perpendicular height, (72 × 2) ÷ 8. Alternatively, divide the area of the triangle by the perpendicular height, and then multiply by two, (72 ÷ 8) × 2. Both calculations give the same answer. The base of the triangle is 18 m.
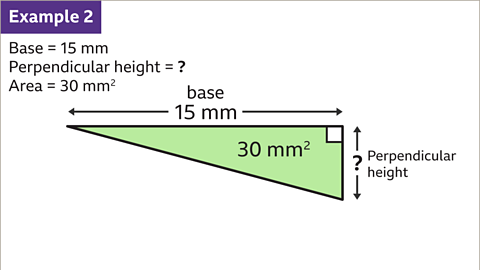
Image caption, The triangle has a base of 15 mm and an area of 30 mm². From this, find the perpendicular height of the triangle.
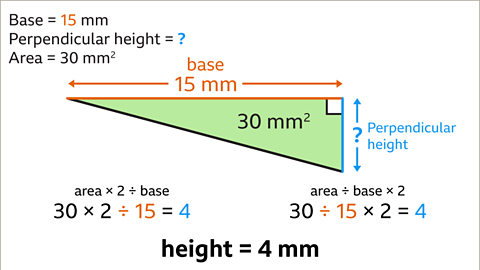
Image caption, Use one of two calculations to work out the perpendicular height. Multiply the area of the triangle by two, then divide by the base, (30 × 2) ÷ 15 = 60 ÷ 15. Alternatively, divide the area of the triangle by the base, and then multiply by two, (30 ÷ 15) × 2 = 2 x 2. Both calculations give the same answer. The perpendicular height of the triangle is 4 mm.
1 of 4
Question
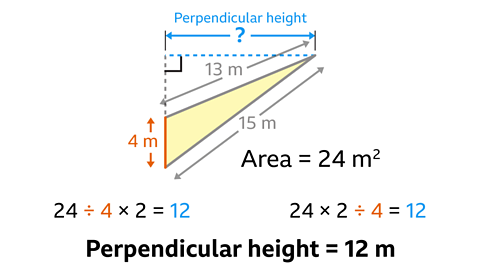
The triangle has an area of 24 m². Find the perpendicular height of the triangle.
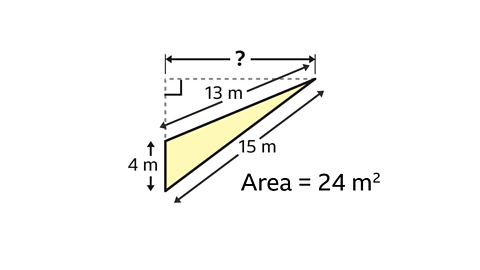
The base of the triangle is perpendicular to its height. The base is 4 m.
The working can be carried out in one of two ways.
height → ÷ 2 → × base → Area
Use the inverse (opposite) operation to find the perpendicular height.
height ← × 2 ← ÷ base ← Area
Divide the area by the base and then multiply by 2(24 ÷ 4) × 2 = 12
The perpendicular height of the triangle is 12 m.
height → × base → ÷ 2 → Area
Use the inverse operations to find the perpendicular height.
height ← ÷ base ← × 2 ← Area
Multiply the area by two and then divide by the base.
(24 × 2) ÷ 4 = 12
The perpendicular height of the triangle is 12 m.
Practise finding the area of triangles
Practise finding the area of triangles with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

A landscape designer may choose to include a triangle-shaped flower bed when creating a new garden layout. To ensure that plants grow well, soil can sometimes require additional nutrients, such as feed or fertiliser.
Nutrients added to soil are used in specific quantities, per unit of area of surface soil.
The landscape designer will need to calculate the area of the triangular flower bed to ensure that the amount of feed or fertiliser used is correct.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Perimeter, Area, Volume
Find out more by working through a topic
- count4 of 11
- count5 of 11
- count6 of 11

- count7 of 11