Key points
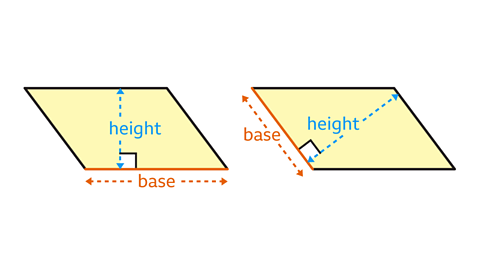
- A parallelogramA quadrilateral with opposite pairs of sides that are both equal in length and parallel. Opposite angles are equal. can be cut and rearranged to form a rectangleA quadrilateral with opposite pairs of sides that are both equal in length and parallel. All four angles are right angles..
- The length and width of the rectangle are the base and height of the parallelogram. The area of a parallelogram is the base multiplied by the perpendicularPerpendicular lines are at 90° (right angles) to each other. height.
- The base of a parallelogram is one of the sides. The perpendicular height is the shortest distance between the base and the opposite parallelAlways equidistant (at equal distances). Parallel lines, curves and planes never meet however far they extend. side.

Find the area of a parallelogram by rearranging it to make a rectangle
Identifying the base and the perpendicular height of a parallelogram:
- The base and the perpendicular height are at right angles.
- One side of the parallelogram is the base.
- The perpendicular height is at right angles to the base.
- The height can be shown inside or outside the parallelogram.
- The base and height may be shown in a different orientation, the base is not necessarily a horizontalA line that is parallel to the horizon. side of the parallelogram.
Showing that a parallelogram has the same area as a rectangle:
- Split the parallelogram into a right-angled triangle and a trapezium.
- Move the triangle to the other end of the shape, making a rectangle.
- The length of the rectangle is the base of the parallelogram. The width of the rectangle is the height of the parallelogram. The shapes have the same area.
The area of the rectangle is found by multiplying the base and the perpendicular height.
The formulaA fact, rule, or principle that is expressed in words or in mathematical symbols. Plural: formulae. for this is \(A = bh\)
Examples
Image caption, Identify the base and height of the parallelogram.
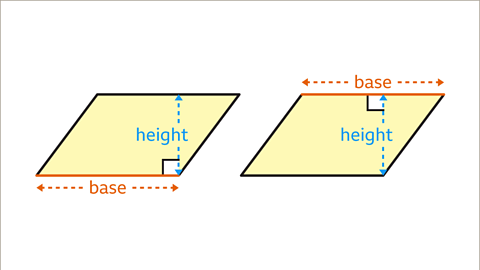
Image caption, The base and the perpendicular height are at right angles. One side of the parallelogram is the base. The base does not have to be the bottom side. The perpendicular height is not a side. It is at right angles to the base and is the shortest distance between the base and the opposite parallel side.
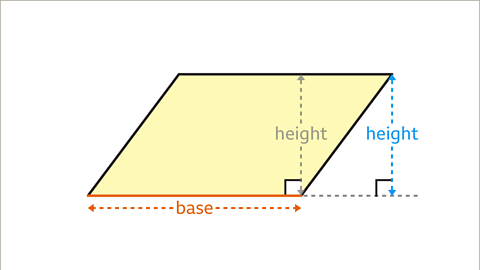
Image caption, The perpendicular height of the parallelogram may be shown inside or outside the shape.
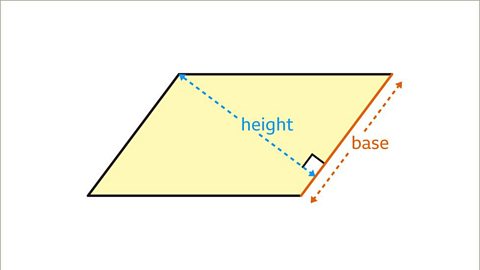
Image caption, The base and perpendicular height may be shown in a different orientation, the base is not necessarily a horizontal side of the parallelogram.
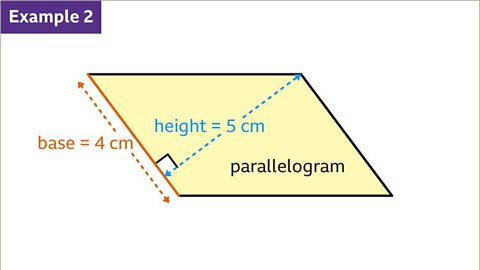
Image caption, Show that the parallelogram above has the same area as a rectangle of base 4 cm and height 5 cm.
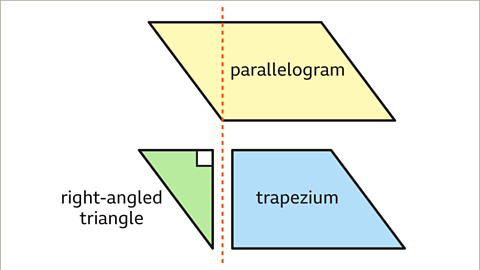
Image caption, To do this, split the parallelogram into a right-angled triangle and a trapezium. A trapezium is a quadrilateral with one pair of parallel sides.
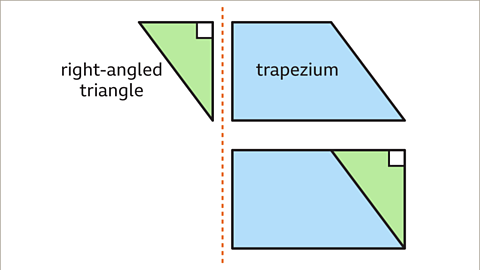
Image caption, Move the right-angled triangle so that the shape becomes a rectangle. The rectangle has the same area as the parallelogram, even though it is a different shape.
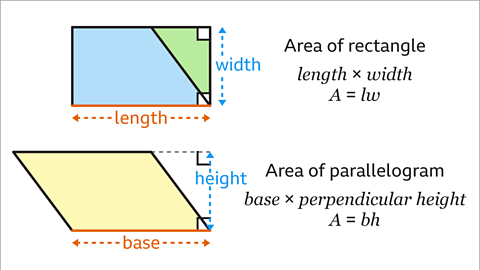
Image caption, The base and height of the rectangle are the base and perpendicular height of the parallelogram. The area of the rectangle is the length multiplied by the width, 𝑨 = 𝒍𝒘. The area of the parallelogram is the base multiplied by the perpendicular height, 𝑨 = 𝒃𝒉.
1 of 8
Question
Decide which of the lettered lengths are the base and perpendicular height of the parallelogram.
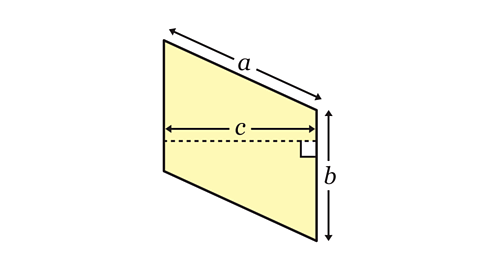
The base and perpendicular height are at right angles to each other. The base is a side of the parallelogram.
The two lettered lengths that are at right angles are \(b\) and \(c\).
\(b\) is a side of the parallelogram and is the base.
\(c\) is the perpendicular height of the parallelogram.
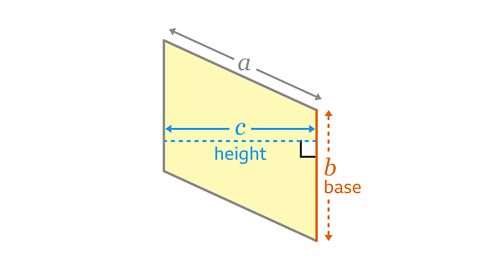
How to calculate the area of a parallelogram
To work out the area of a parallelogram:
- Identify the base and the perpendicularPerpendicular lines are at 90° (right angles) to each other. height of the parallelogramA quadrilateral with opposite pairs of sides that are both equal in length and parallel. Opposite angles are equal..
- Check that the base and height are measured in the same units.
- If necessary, convert the measurements so that the units match. When working in millimetres, a 1۰2 cm measurement would be converted to 12 mm.
- Substitute the values of the base, \(b\), and the perpendicular height, \(h\), into the formula \(A = bh\).
- Multiply the base and the perpendicular height.
- Write down the answer with the appropriate square units.
Examples
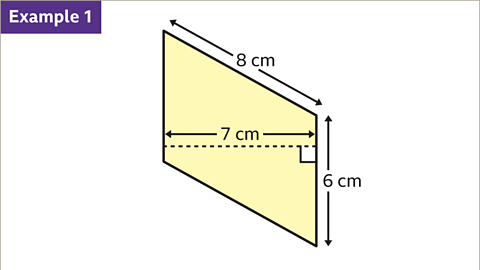
Image caption, Find the area of the parallelogram.
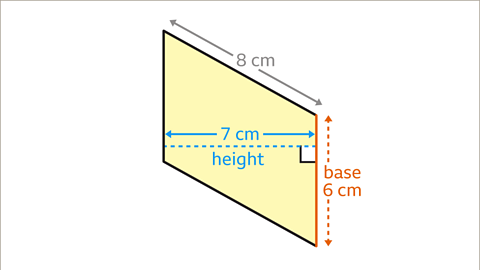
Image caption, The base and the perpendicular height are at right angles to each other. The base is 6 cm and the perpendicular height is 7 cm. They are in the same units.
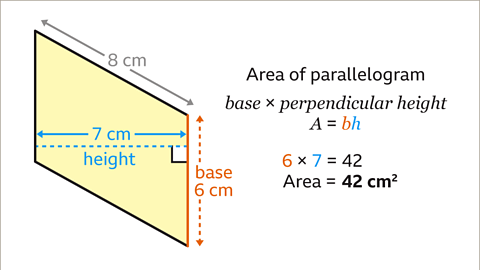
Image caption, The area of a parallelogram is the base multiplied by the perpendicular height. Substitute the values for the base and the perpendicular height into the formula 𝑨 = 𝒃𝒉, so 6 × 7 = 42. The area of the parallelogram is 42 cm².
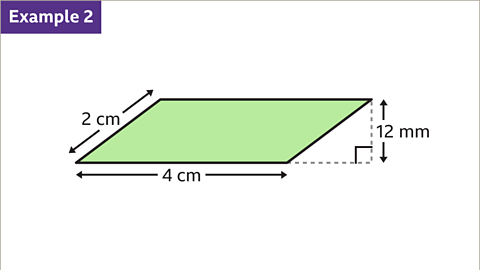
Image caption, Work out the area of the parallelogram.
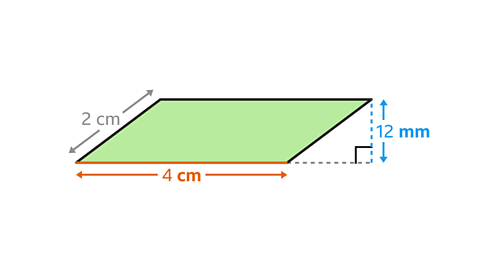
Image caption, The base and perpendicular height are at right angles to each other. The base is 4 cm and the perpendicular height is 12 mm. They are not in the same units. They need to be converted so that the units match.
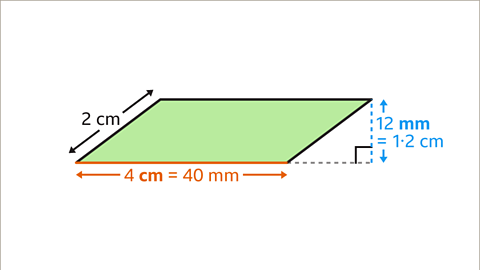
Image caption, The area must be worked out using the same units. This may be in mm² or in cm². 4 cm is 40 mm. 12 mm is 1۰2 cm.
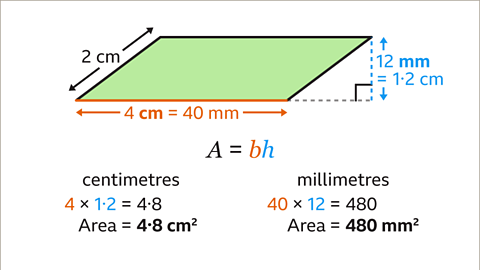
Image caption, Work either in centimetres or in millimetres. Use the formula by substituting the base and perpendicular height values. In centimetres, 4 cm × 1۰2 cm = 4۰8 cm. The area is 4۰8 cm². In millimetres, 40 mm × 12 mm = 480 mm. The area is 480 mm².
1 of 7
Question
Work out the area of the parallelogram.
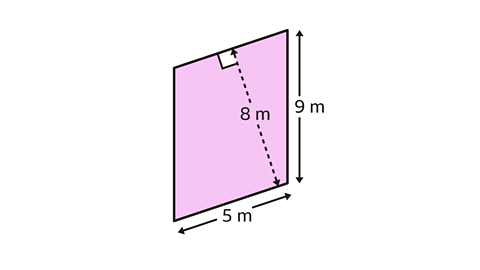
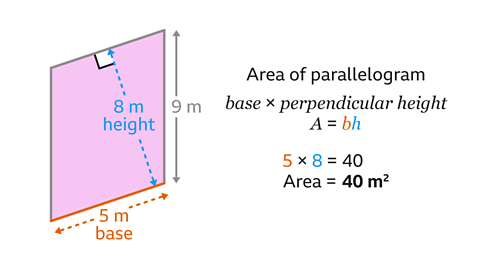
The base and perpendicular height are at right angles to each other. The two measurements at right angles are 8 m and 5 m.
The base is one side of the parallelogram, 5 m. The perpendicular height is at right angles to the base and measures 8 m.
Substitute the base and height values into the formula.
The area of the parallelogram is the base multiplied by the perpendicular height.5 × 8 = 40
The area of the parallelogram is 40 m².
How to calculate the base or perpendicular height, given the area
The area of a parallelogram is the base multiplied by the perpendicular height. To find either the base or the perpendicular height, use the inverse of multiplication, which is division.
To calculate the base of a parallelogram:
- Divide the area by the perpendicular height.
To calculate the perpendicular height of a parallelogram:
- Divide the area by the base.
Sometimes a maths problem may involve needing to work out the area first.
Examples
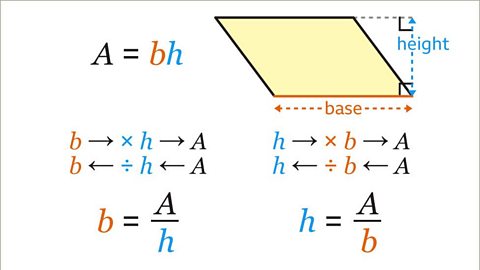
Image caption, The area of a parallelogram is the base multiplied by the perpendicular height. To find either the base or the perpendicular height, use the inverse operation. The inverse of multiply by the perpendicular height is divide by the perpendicular height. The base is the area divided by the perpendicular height. The inverse of multiply by the base is divide by the base. The perpendicular height is the area divided by the base.
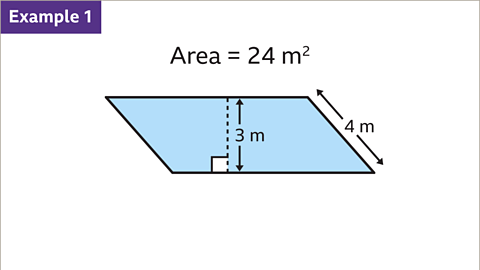
Image caption, The parallelogram has an area of 24 m². Find the length of the base of the parallelogram.
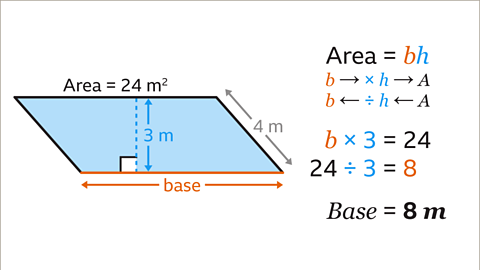
Image caption, The base and the perpendicular height are at right angles. The perpendicular height is 3 m. The base multiplied by the perpendicular height gives the area of the parallelogram. The base multiplied by 3 is 24 m². The inverse of multiply by 3 is divide by 3. Divide the area by the perpendicular height. 24 ÷ 3 = 8. The length of the base of the parallelogram is 8 m.
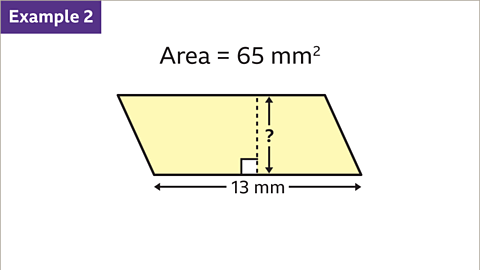
Image caption, The parallelogram has an area of 65 mm². The base is 13 mm. Find the perpendicular height of the parallelogram.
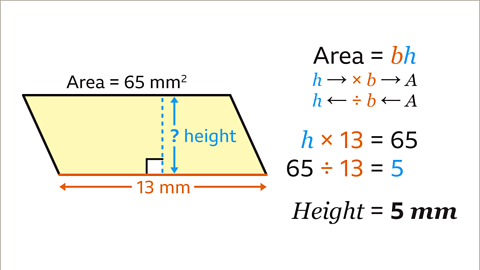
Image caption, The base and the perpendicular height are at right angles to each other. The base is 13 mm. The base multiplied by the perpendicular height gives the area of the parallelogram. This is the same as the perpendicular height multiplied by the base. The perpendicular height multiplied by 13 is 65. The inverse of multiply by 13 is divide by 13. Divide the area by the base. 65 ÷ 13 = 5. The perpendicular height of the parallelogram is 5 mm.
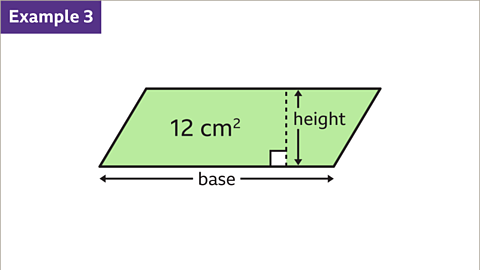
Image caption, A parallelogram has a height which is one third of the length of the base. The area of the parallelogram is 12cm². Find the base and height of the parallelogram.

Image caption, The area of a parallelogram is the base multiplied by the height. The area of the parallelogram is 12 cm². Factor pairs of 12 are integer values that multiply to give 12. The factor pairs of 12 are 1 and 12, 2 and 6, and 3 and 4. The values of the base and height could be either of each pair of values. The base is the larger value so the factor pairs to choose between are 4 and 3, 6 and 2 and 12 and 1
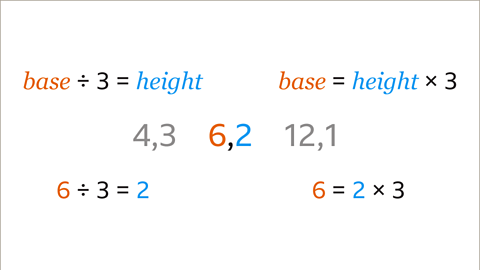
Image caption, The height of the parallelogram is one third of its base, base ÷ 3 = height. This is the same as base = height × 3. 6 ÷ 3 = 2 and 6 = 2 × 3
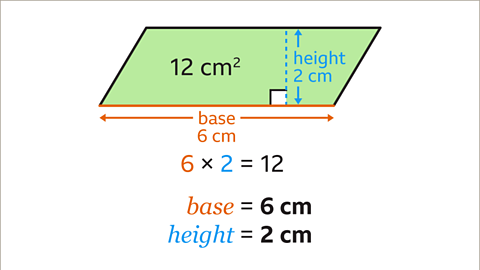
Image caption, The parallelogram has an area of 12 cm² and a height that is one third of its base. 6 × 2 = 12. The area of the parallelogram is 12 cm². The base of the parallelogram is 6 cm, and its height is 2 cm.
1 of 9
Question
The area of the parallelogram is 200 mm². Work out the perpendicular height of the parallelogram.
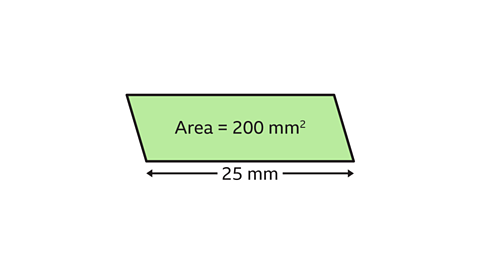
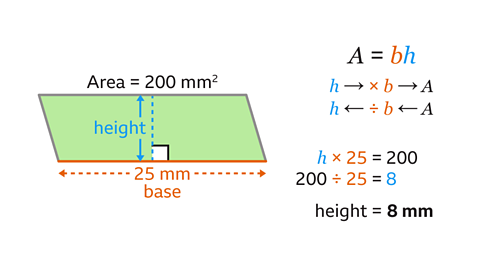
The base and the perpendicular height are at right angles. The base is 25 mm.
The base multiplied by the perpendicular height gives the area of the parallelogram. This is the same as the perpendicular height multiplied by the base.
The perpendicular height multiplied by 25 mm is 200 mm². The inverse of multiply by 25 is divide by 25
Divide the area by the base. 200 mm ÷ 25 mm = 8 mm. The perpendicular height of the parallelogram is 8 mm.
Practise finding the area of parallelograms
Practise finding the area of parallelograms with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

Tile manufacturers sell different types of tiles that are parallelogram-shaped.
The total area that the tiles contained in a pack will cover is given on its packaging. This helps a customer buying the tiles to know how many packs they should get in order to cover a wall or floor.
The manufacturer will need to know the area of each parallelogram-shaped tile to be able to give the customer this information.
Lots of arrangements that are possible with parallelogram-shaped tiles can produce designs that are really creative and often more unusual to look at than regular rectangular-shaped tiles.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Perimeter, Area, Volume
Find out more by working through a topic
- count5 of 11
- count6 of 11

- count7 of 11
- count8 of 11