Key points
While rectangles look alike and are easily recognisable, trapeziumA quadrilateral with exactly one pair of parallel sides. can look very different to each other.
Two identical trapeziums can be combined to make a parallelogramA quadrilateral with opposite pairs of sides that are both equal in length and parallel. Opposite angles are equal. or a rectangle. The areaA measure of the size of any plane surface or 2D shape. Area is measured in square units, for example, square centimetres or square metres: cm² or m². of the trapezium is half of the parallelogram or rectangle.
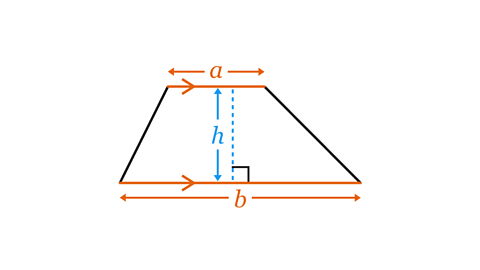
Recognising the parallelAlways equidistant (at equal distances). Parallel lines, curves and planes never meet however far they extend. sides and the perpendicularPerpendicular lines are at 90° (right angles) to each other. height are key in working out the area of a trapezium. The area of a trapezium is the average length of its parallel sides multiplied by the perpendicular height. This is shown by the formulaA fact, rule, or principle that is expressed in words or in mathematical symbols. Plural: formulae. 𝑨 = ½ (𝒂 + 𝒃)𝒉.
The parallel sides of a trapezium are labelled 𝒂 and 𝒃. The perpendicular height is the shortest distance between the parallel sides and is labelled 𝒉.

Video
Watch the video to learn how to work out the area of a trapezium.
Calculating the area of a trapezium is a little different to calculating the area of a rectangle, because a trapezium does not have two pairs of equal sides. But a trapezium can be looked at as half a parallelogram. The area of a parallelogram can be measured by multiplying its length by its perpendicular height.
Because if one end were chopped off, it would fit perfectly at the other end. When a triangle is chopped off a rectangle and moved to the other end, a parallelogram is formed. The area of the parallelogram is the same as the area of the rectangle.
Back to the trapezium, or trapeziums, since we have now created two by splitting the parallelogram in half.
Labelling the diagram to show each distinct edge demonstrates that an easy way to calculate the area of a trapezium is to calculate the area of the resulting parallelogram. That gives us the area for two trapeziums. So, to get the area for just the one, we divide that total by two.
In other words, the sum of 𝑎 + 𝑏 × 𝘩, all divided by two.
Understanding the formula for the area of a trapezium
To find the area of a trapezium:
- Draw two congruentA shape that has a mathematical change of appearance. trapeziums.
- Rotate one trapezium by 180°.
- Put the two trapeziums together to form a parallelogram.
- The area of the parallelogram is the base multiplied by the perpendicular height. The base of the parallelogram is the total of the two parallel sides of the trapezium, (𝒂 + 𝒃). The area of the parallelogram is (𝒂 + 𝒃)𝒉.
- The area of the trapezium is half of the area of the parallelogram. The formula is½(𝒂 + 𝒃)𝒉.
When the trapezium has two right angles, the two congruent trapeziums make a rectangle.
Examples
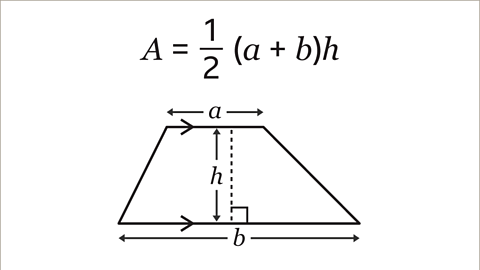
Image caption, The formula for the area (𝑨) of a trapezium is 𝑨=½ (𝒂 + 𝒃)𝒉.
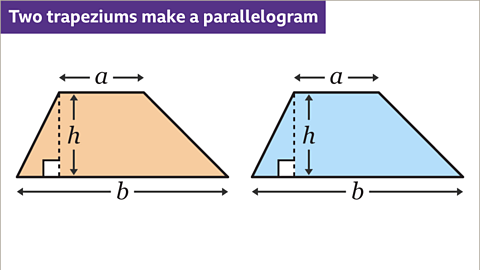
Image caption, Draw two congruent (identical) trapeziums.
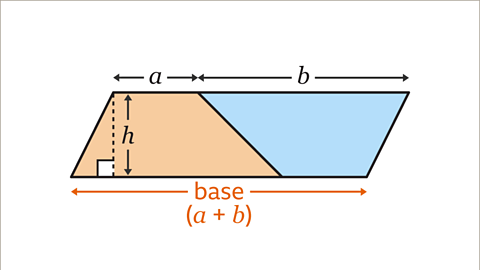
Image caption, Rotate one trapezium by 180° and put the two trapeziums together to form a parallelogram. The base of the parallelogram is the total length of the parallel sides of the trapezium, 𝒃 + 𝒂 = 𝒂 + 𝒃. The perpendicular height of the parallelogram is the height (𝒉) of the trapezium.
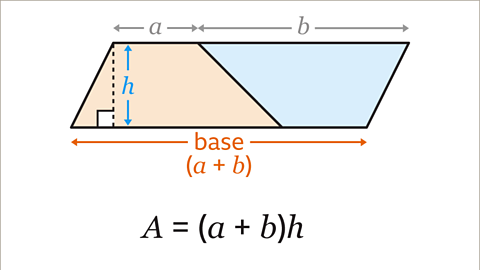
Image caption, The area of the parallelogram is the base multiplied by the height. (𝒂 + 𝒃) × 𝒉. This can be written without the multiplication symbol as (𝒂 + 𝒃)𝒉
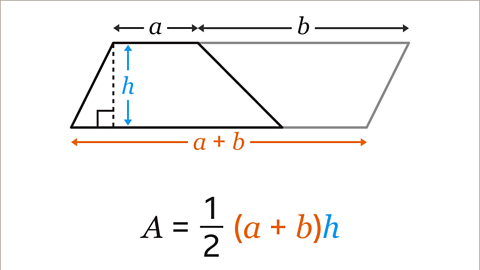
Image caption, The area of the trapezium is half of the area of the parallelogram. The formula can be written as 𝑨 = ½ (𝒂 + 𝒃)𝒉 or 𝑨 = (𝒂 + 𝒃)𝒉/2
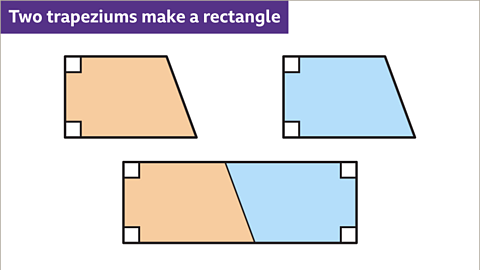
Image caption, When the trapezium has two right angles, two congruent trapeziums can be put together to make a rectangle.
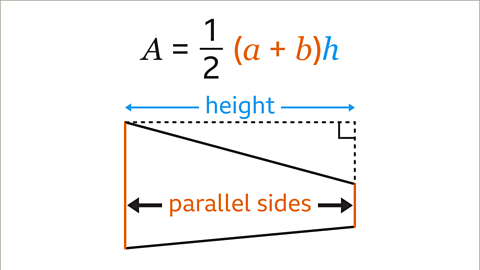
Image caption, To use the formula 𝑨 = ½ (𝒂 + 𝒃)𝒉, the parallel sides and the perpendicular height must be identified.
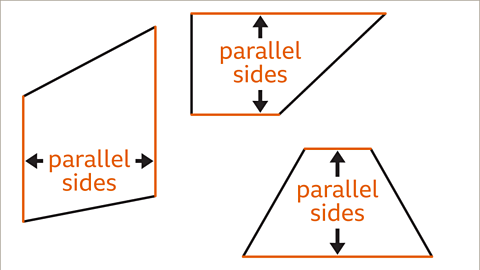
Image caption, The parallel sides are always on opposite sides of the trapezium. They are the same distance apart throughout their length.
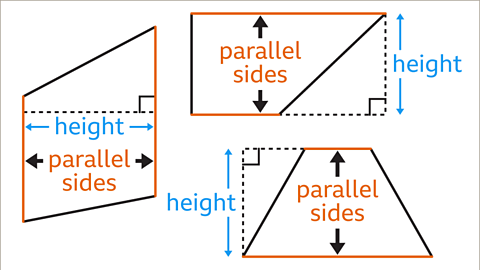
Image caption, The height is the shortest distance between the parallel sides. The height meets the parallel sides at right angles.
1 of 9
Question
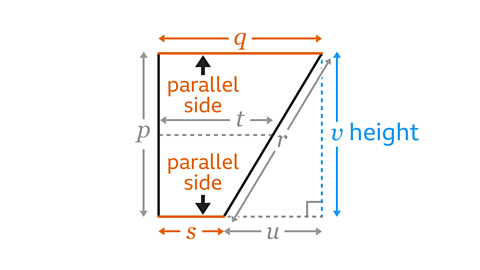
Identify the parallel sides and the height for this trapezium.
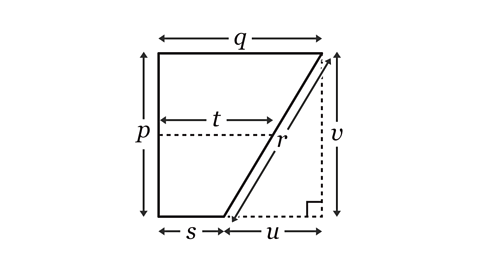
The parallel sides are 𝒒 and 𝒔. The parallel sides are a fixed distance apart throughout their length.
The height is the line labelled 𝒗. The height is the shortest distance between the parallel sides. The height is at right angles to the parallel sides.
Calculating the area of a trapezium
To calculate the area of a trapezium:
Identify the parallel sides 𝒂 and 𝒃, and the perpendicular height, 𝒉.
Substitute the values of 𝒂, 𝒃 and 𝒉 into the formula.
Complete the calculation. Remember that the result is an area so the units are square centimetres (cm²).
Example
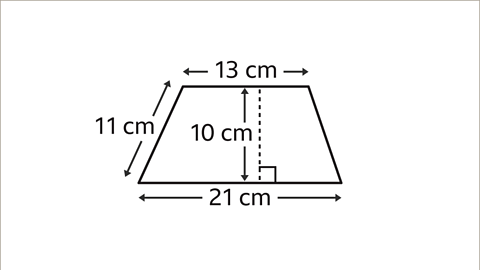
Image caption, Find the area of the trapezium.
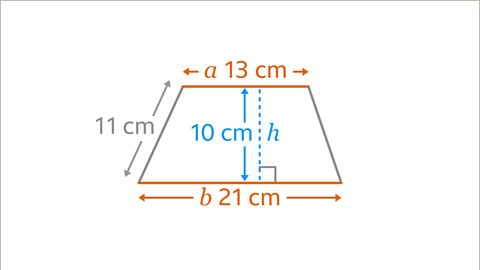
Image caption, Identify the parallel sides 𝒂 and 𝒃, and the perpendicular height (𝒉). The parallel sides are 13 cm and 21 cm. The height is at right angles to the parallel sides. The height is 10 cm.
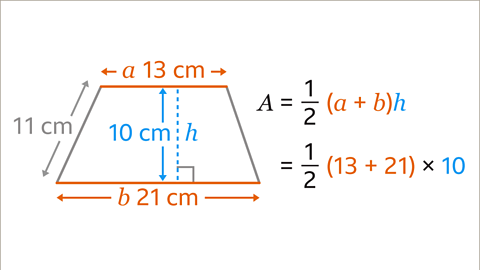
Image caption, Substitute the values of 𝒂, 𝒃, and 𝒉 into the formula for the area of a trapezium.

Image caption, Add the lengths of the parallel sides. 13 + 21 = 34. Then divide by two and multiply by the height. 34 ÷ 2 × 10 = 170. The area of the trapezium is 170 cm²
1 of 4
Question
Work out the area of the trapezium.
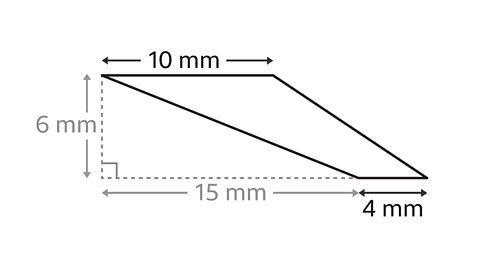
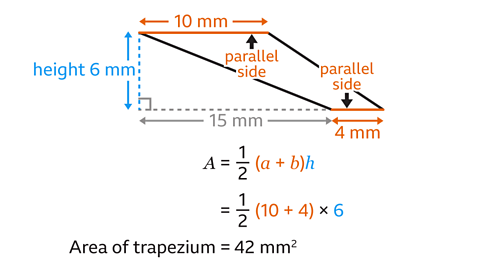
- Identify the parallel sides 𝒂 and 𝒃, and the perpendicular height, 𝒉.
- The parallel sides are 10 mm and 4 mm.
- The height is at right angles to the parallel sides.
- The height is 6 mm.
- Substitute the values for 𝒂, 𝒃, and 𝒉 into the formula for the area of a trapezium.
- Complete the calculation.
½ (10+4) × 6 = 42
The area of the trapezium is 42 mm²
Practise finding the area of trapeziums
Practise finding the area of trapeziums with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

Plasterers are skilled tradespeople who apply plaster and decorative finishes to walls and ceilings. Walls are covered with plaster so that further decoration goes onto a smooth surface.
An attic converted to a bedroom can have trapezium-shaped walls. The amount of plaster used depends on the area of the walls, so knowing how to work out the area of a trapezium is important. It will also impact on how much time a plasterer will need to finish the job and therefore how much it will cost overall.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Perimeter, Area, Volume
Find out more by working through a topic
- count6 of 11

- count7 of 11
- count8 of 11
- count9 of 11