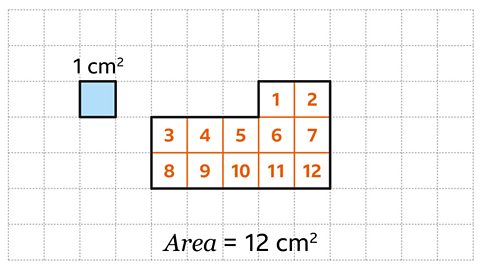
Key points
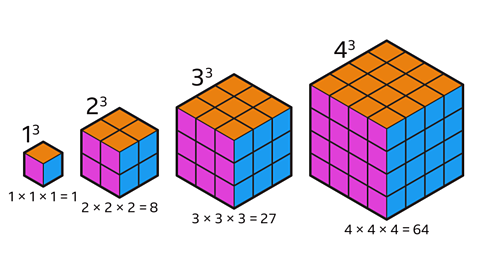
volumeThe amount of space a 3D shape takes up. A cubic cm block takes up 1 cubic cm. and capacityThe volume of a material (typically liquid or air) held in a vessel or container. are measured in cubic units, including cm³ and m³.
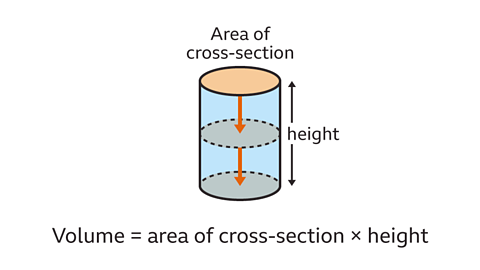
To calculate volume and capacity, three dimensions are used: length, width and height.
When a cubeA 3D shape with six square faces. or cuboidA 3D shape with six rectangular faces. The opposite faces are congruent. is drawn using individual cubes, the volume can be found by counting the unit cubeA cube representing a fixed volume, such as 1 cm³ or 1 m³.. This method can also be used for compound 3D shapes made up of two or more cuboids.
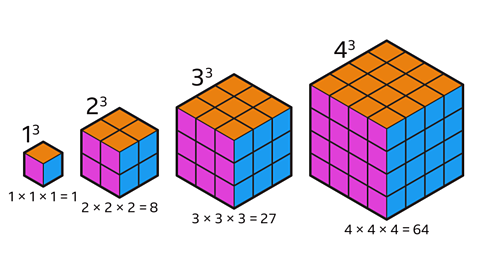
Finding volume by counting cubes and using cube numbers
Volume is measured in cubic units. These are unit cubes which may be mm³, cm³ and m³.
There are multiple ways of finding the volume of a cube. For example, counting the cubes of the top layer and by cubing one of the cube’s sides.
To find the volume by counting cubes:
Count the unit cubes that make the top layer of the cube.
Multiply the number of cubes in the top layer by the total number of layers it has.
To calculate the volume of a cube:
- Cube the length of one edge of the cube. For an edge of length \(x\), the volume of a cube is given by the formula \(V\) = \(x\)³.
To calculate the edge of a cube:
- cube rootThe cube root of a number is a special value that, when used in a multiplication three times, gives that number. Eg, 3 × 3 × 3 = 27, so the cube root of 27 is 3 the volume. Cube root is the inverseThe opposite of a mathematical process. E.g. the inverse of × 5 is ÷ 5. The inverse process undoes the original process. of cube.
Examples
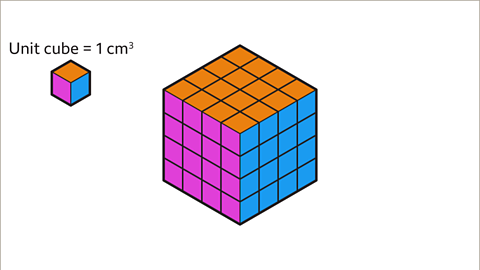
Image caption, Volume is measured in cubic units. Each unit cube represents 1 cm³. Find the volume of the cube.
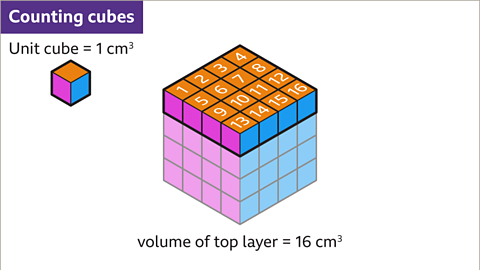
Image caption, Count the number of cm³ in the top layer. There are 16 unit cubes. The top layer of the cube has a volume of 16 cm³.
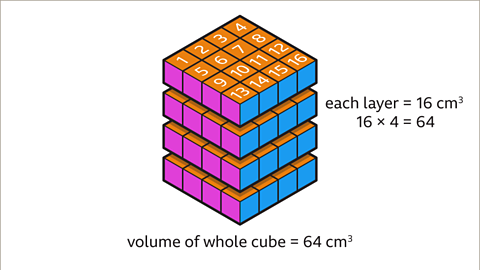
Image caption, Each layer has the same number of cm³. Each layer is 16 cm³. There are four layers. Multiply the number of cm³ in each layer by the number of layers. 16 × 4 = 64. The volume of the cube is 64 cm³.
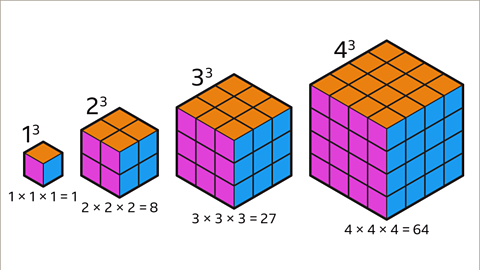
Image caption, The volume of a cube with a whole number edge length is a cube number. A cube number is the result of a number multiplied by itself and multiplied by itself again. The first four cube numbers are 1, 8, 27, 64
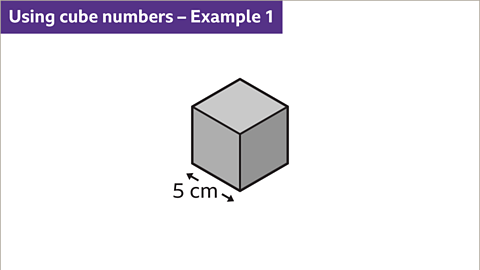
Image caption, Calculate the volume of the cube.
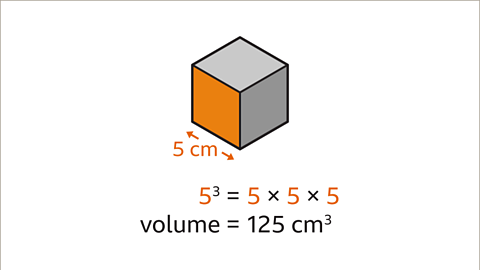
Image caption, Cube the length of the edge of the cube. The edge of the cube measures 5 cm. 5³ = 5 x 5 x 5. The volume of the cube is 125 cm³.
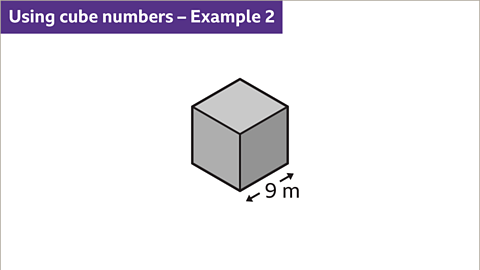
Image caption, Calculate the volume of the cube.
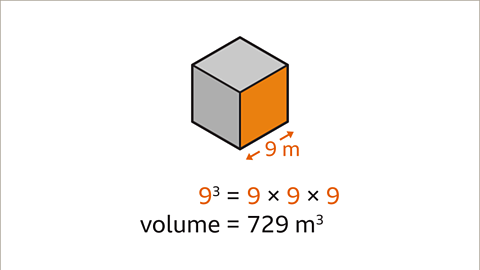
Image caption, Cube the length of the edge of the cube. The edge of the cube measures 9 m. 9³ = 9 x 9 x 9. The volume of the cube is 729 m³.
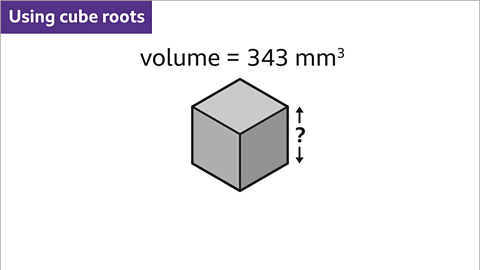
Image caption, The volume of the cube is 343 mm³. How long is one edge of the cube?
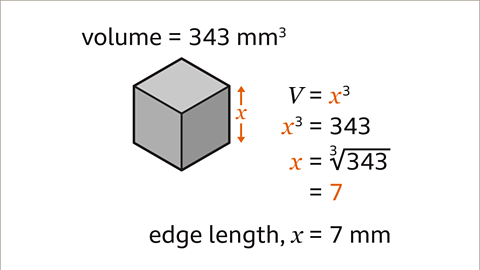
Image caption, The formula for the volume of a cube is 𝑽 = 𝒙³, where 𝒙 (the edge of the cube) is cubed. The inverse of cube is cube root. Cube root the volume to find the edge length. ∛343 = 7 (7 × 7 × 7 = 343). The edge of the cube is 7 mm.
1 of 10
Question
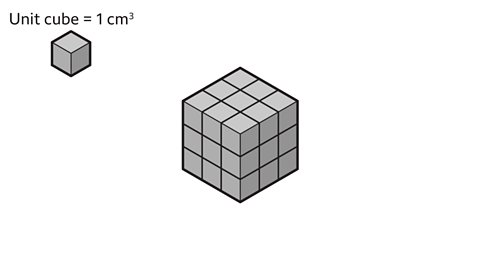
Each unit cube is 1 cm³. Find the volume of the cube.
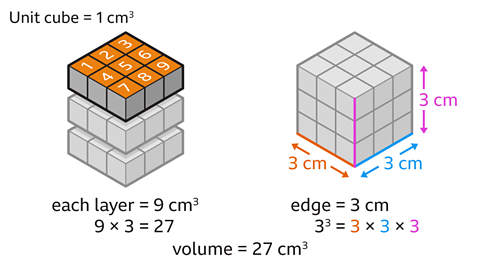
To find the volume by counting the cubes:
Count the cm³ on the top layer. The top layer has a volume of 9 cm³
Multiply the number of cm³ on the top layer by the number of layers.
9 × 3 = 27. The volume of the cube is 27 cm³.
- To calculate the volume of the cube:
Calculate the volume of the cube by cubing the edge length of the cube. The edge length is 3 cm.
3³ = 27. The volume of the cube is 27 cm³.
Calculating the volume of a cuboid
- To find the volume of a cuboid by counting:
Count the unit cubes that make the top layer of the cuboid.
Multiply the number of cubes in the top layer by the number of layers.
To calculate the volume of a cuboid:
- Multiply the length by width by height. \(V\) = \(lwh\). This can be done in any order, the answer will be the same.
Examples
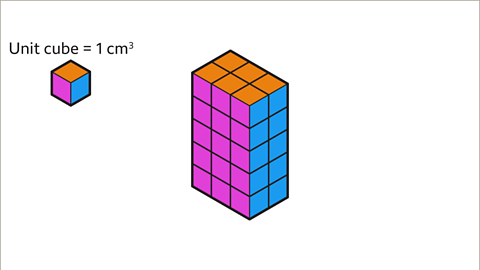
Image caption, Each unit cube represents 1 cm³. Find the volume of the cuboid.
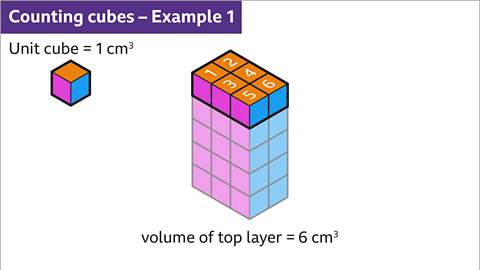
Image caption, Count the number of cm³ in the top layer. There are 6. The top layer of the cube has a volume of 6 cm³. Each layer has the same number of cm³. Each layer is 6 cm³.
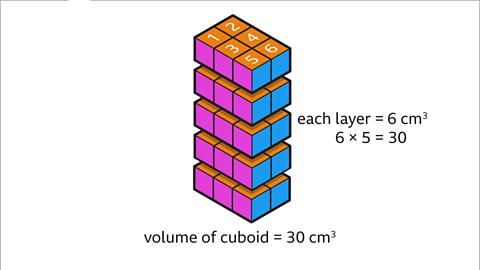
Image caption, Multiply the number of cm³ in each layer by the number of layers. There are 5 layers. 6 × 5 = 30. The volume of the cuboid is 30 cm³.
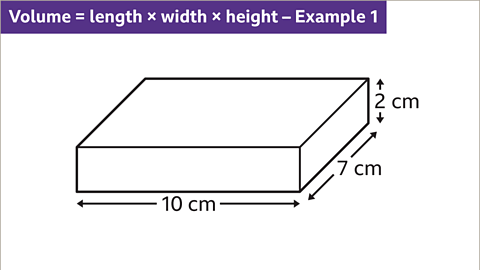
Image caption, Calculate the volume of the cuboid.
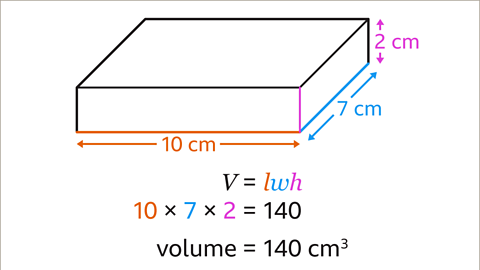
Image caption, Multiply the length by width by height. 10 × 7 × 2 = 140. The volume of the cuboid is 140cm³.
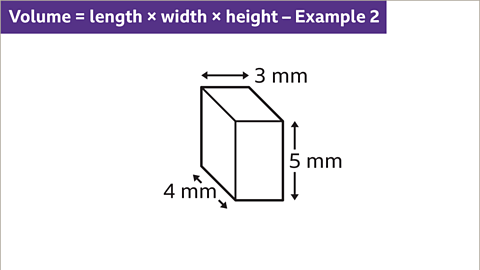
Image caption, Calculate the volume of the cuboid.
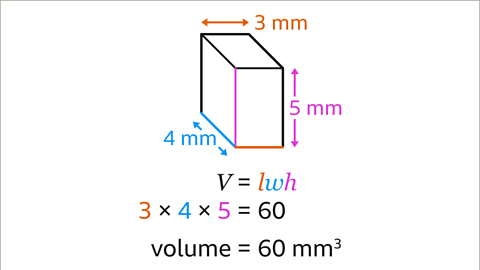
Image caption, Multiply the length by width by height. 3 × 4 × 5 = 60. The volume of the cuboid is 60cm³.
1 of 7
Question
What is the volume of the cuboid?
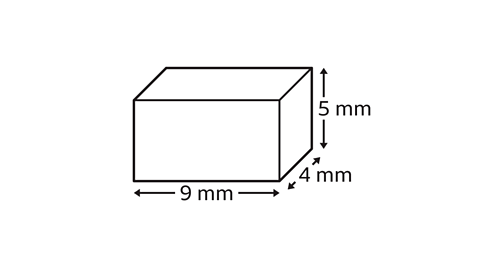
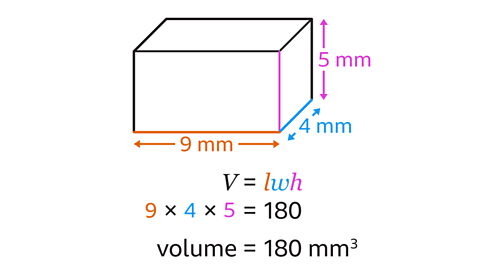
The volume of a cuboid is length × width × height.
9 × 4 × 5 = 180
The volume of the cuboid is 180 mm³.
Practise finding the volume of cubes and cuboids
Practise finding the volume of cubes and cuboids with the quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

A delivery service should ensure that the boxes used have the capacity to hold the articles that have been purchased. The cost of sending a package can be related to its volume. This may be referred to as volumetric weight.
Volumetric weight is used in the courier and logistics industry to calculate how much space an item is going to take up. If your item is light in weight but large in size, and therefore takes up a lot of room, the cost charged will reflect this.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Perimeter, Area, Volume
Find out more by working through a topic
- count10 of 11
- count11 of 11
- count1 of 11
- count2 of 11