Key points
A prismA 3D shape with a constant polygon cross-section. has a constant cross-sectionThe face that results from slicing through a solid shape. . The cross-section is a polygonA closed 2D shape bounded by straight lines..
The surface area (of a 3D shape)The total area of all the faces of a 3D shape. Measured in square units, such as cm² and m². is made up of congruentShapes that are the same shape and size, they are identical.faceOne of the flat surfaces of a solid shape. at either end of the prism and a set of rectangles between them. The number of rectangular faces is the same as the number of EdgeThe line formed by joining two vertices of a shape. The line formed when two faces meet. of the shape at each end of the prism.
Understanding netA group of joined 2D shapes which fold to form a 3D shape. of surface area (of a 3D shape)The total area of all the faces of a 3D shape. Measured in square units, such as cm² and m². shapes and the area of different shapes helps when working out the surface area of a prism. Surface area is measured in square units, such as cm² and mm².
The volumeThe amount of space a 3D shape takes up. A cubic cm block takes up 1 cubic cm. of a prism is the area of its cross-section multiplied by the length. Volume is measured in cubed units, such as cm³ and mm³.

How to calculate the surface area of a prism
A prismA 3D shape with a constant polygon cross-section. can be named by the shape of its polygonA closed 2D shape bounded by straight lines.cross-sectionThe face that results from slicing through a solid shape. .
- When the cross-section is a triangle, the prism is called a triangular prism.
- When the cross-section is a hexagon, the prism is called a hexagonal prism.
A cylinderA 3D shape with a constant circular cross-section. is not a prism. The cross-section of a prism is a polygon, a shape bounded by straight lines. A circle is not a polygon.
The surface area is made up of the end faces and rectangular faces that join them.
- To calculate the total surface area of a prism:
- Find the area of the two end faces.
- Work out the area of all the rectangular faces in one of two ways:
- Work out the area of each rectangle separately, length × width.
- Multiply the perimeter of the end face by the length of the prism.
- Sum the areas of all the faces.
Examples
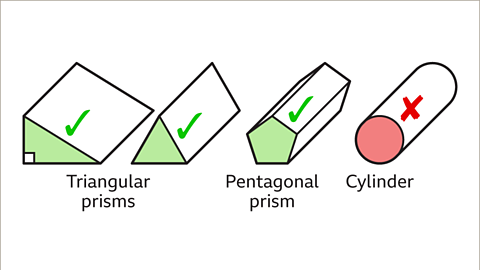
Image caption, A prism has a uniform cross-section. That means that the cross-section is the same throughout the length of the prism. The polygon shape of the cross-section may be used to name the prism. A prism with a triangle-shaped cross-section is a triangular prism. A prism with a pentagon-shaped cross-section is a pentagonal prism. A 3D shape with a circular cross-section is a cylinder. A cylinder is not a prism because the circle is not a polygon.
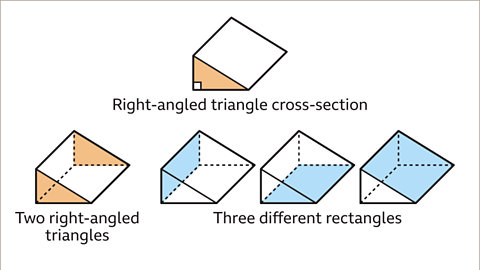
Image caption, The total surface area of a prism is made up of the areas of the two end faces and the rectangles that join them.
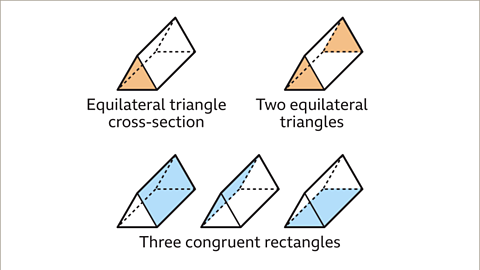
Image caption, For a prism with a regular polygon cross-section, the rectangles are congruent (identical).
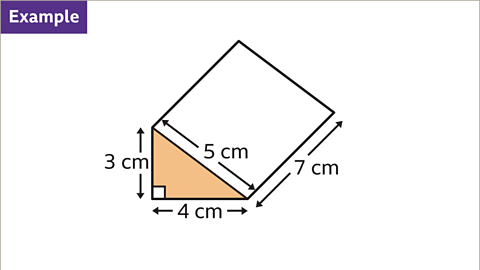
Image caption, Calculate the total surface area of the triangular prism.
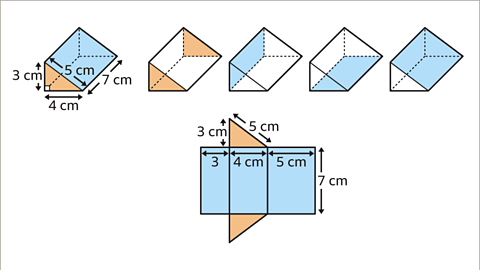
Image caption, The total surface area of the prism is made up of two congruent triangles and three differently sized rectangles. This may be shown by a net of the prism.
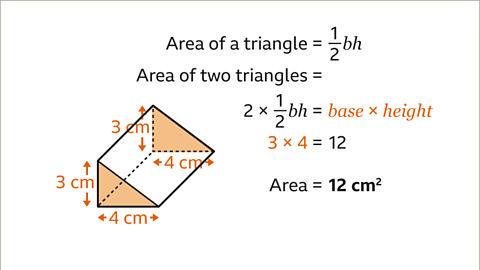
Image caption, First work out the area of the triangular faces. The area of a triangle is ½ × base × height. There are two congruent (identical) triangles, so 2 × ½ × base × height = base × height. 3 × 4 = 12. The area of the triangular faces is 12 cm².
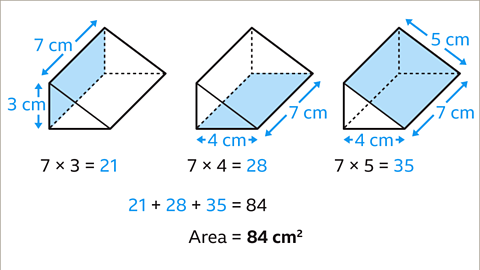
Image caption, Next work out the areas of the rectangular faces. The area of a rectangle is length multiplied by width. 7 × 3 = 21, 7 × 4 = 28, 7 × 5 = 35. These areas are added together. 21 + 28 + 35 = 84. The area of all the rectangular faces is 84 cm².
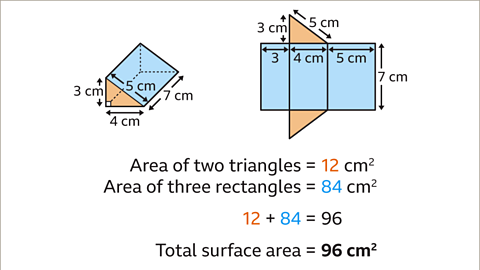
Image caption, Sum the area of the end faces and the rectangular faces. 12 + 84 = 96. The total surface area of the prism is 96 cm².
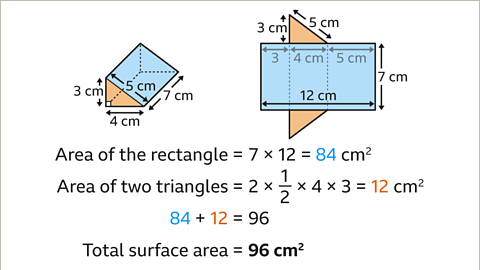
Image caption, The rectangular faces can be combined to form one rectangle. One edge of the rectangle is the perimeter of the triangle. 3 + 4 + 5 = 12. The area of the combined rectangular faces is 7 × 12 = 84 cm². The area of the triangular faces is 12 cm². The areas of the faces are summed, 84 + 12 = 96. The total surface area of the prism is 96 cm².
1 of 9
Questions
Question 1: Find the total surface area of the prism.
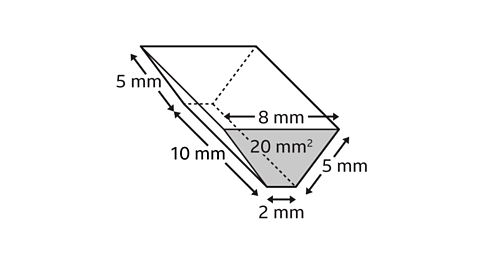
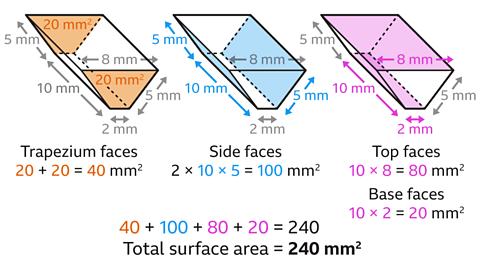
The area of the trapezium-shaped cross-section is given, 20 mm².
The surface area of the prism is made up of two trapezium-shaped faces and four rectangular faces.
The area of the two trapeziums is 2 × 20 = 40 mm².
The area of the two side rectangular faces is 2 × 10 × 5 = 100 mm².
The area of the top rectangle is 10 × 8 = 80 mm².The area of the base rectangle is 10 × 2 = 20 mm².
The areas of all the faces are added together.40 + 100 + 80 + 20 = 240
The total surface area of the prism is 240 mm².
Question 2: Find the total surface area of the triangular prism.

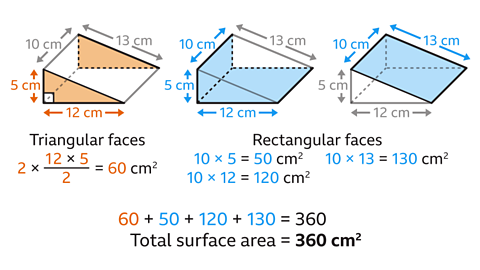
The surface area of the prism is made up of five faces, which are two right-angled triangles and three rectangles.
The area of each triangular face is \(\frac{12×5}{2}\) = 30 cm².The area of the rectangular faces are10 × 5 = 50 cm², 10 × 12 = 120 cm² and 10 × 13 = 130 cm².
The total surface area is the total of all the individual faces.
30 + 30 + 50 + 120 + 130 = 360 cm².
How to calculate the volume of a prism
The formula for the volumeThe amount of space a 3D shape takes up. A cubic cm block takes up 1 cubic cm. of a prism is:
\(Volume =\) \(Area\) \(of\) \(cross\)-\(section\) × \(length\)
To calculate the volume of a prism:
- Work out the area of the cross-sectionThe face that results from slicing through a solid shape. .
- Multiply by the length (or height) of the prism.
Examples
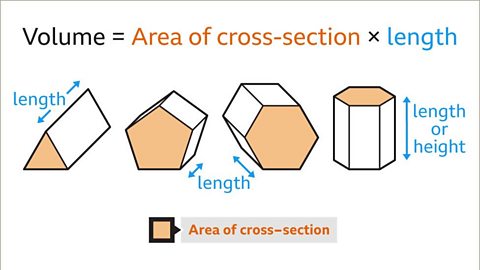
Image caption, The volume of a prism is the area of the cross-section multiplied by the length. The length may be the height, depending on the orientation of the prism.
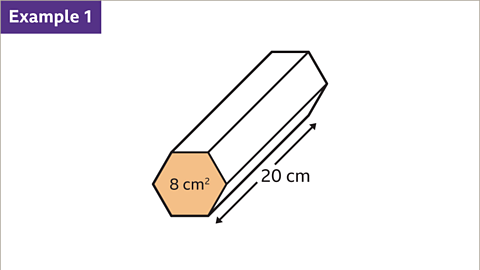
Image caption, Find the volume of the prism.
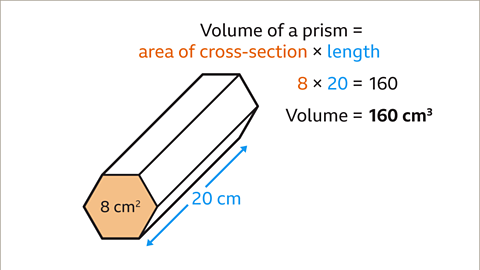
Image caption, The area of the cross-section is given, 8 cm². The area of the cross-section is multiplied by the length, 8 × 20 = 160. The volume of the prism is 160 cm³.
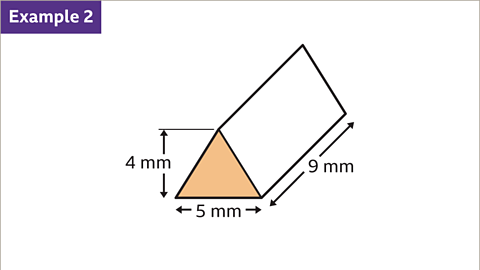
Image caption, Work out the volume of the prism.
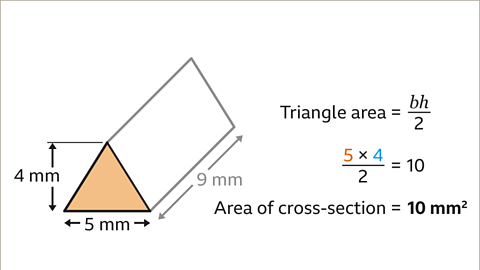
Image caption, The cross-section of the prism is a triangle. First work out the area of the triangle. Multiply the base by the height and divide by two, (5 × 4)/2 = 10. The area of the triangular cross-section is 10 mm².
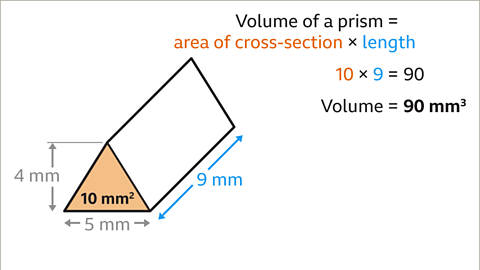
Image caption, Next multiply the area of the cross-section by the length of the prism. 10 × 9 = 90. The volume of the prism is 90 mm³.
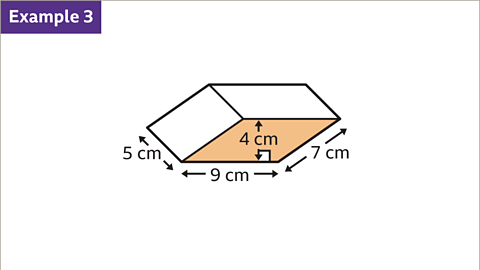
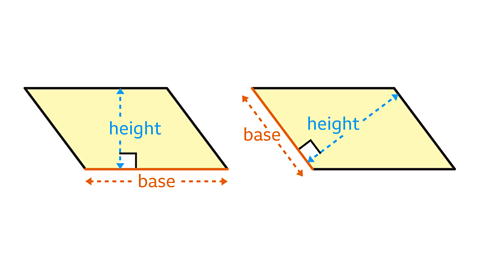
Image caption, The cross-section of the prism is a parallelogram. Work out the volume of the prism.
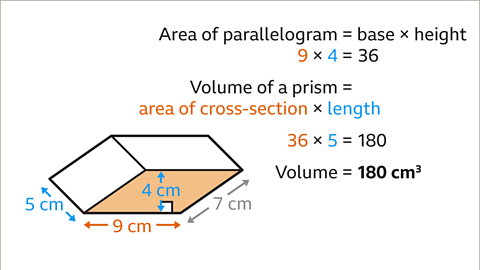
Image caption, The area of the parallelogram is the base multiplied by the height. 9 × 4 = 36. The volume of the prism is the area of the cross-section multiplied by its length. 36 × 5 = 180. The volume of the prism is 180 cm³.
1 of 8
Question
Find the volume of the prism.
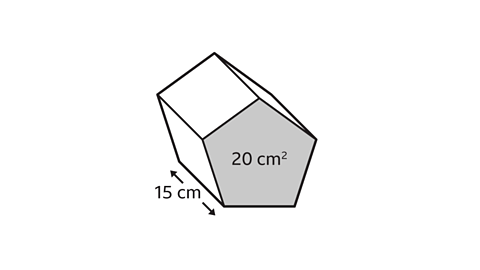
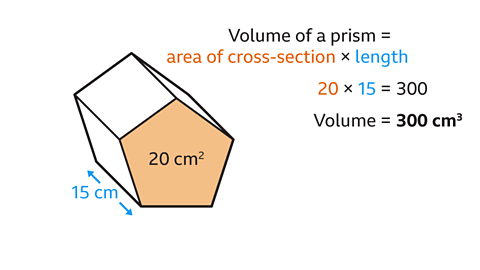
The area of the pentagonal cross-section is given, 20 cm².The length of the prism is 15 cm.
The volume of the prism is the area of the cross-section multiplied by the length.20 × 15 = 300
The volume of the prism is 300 cm³.
Practise finding the surface area and volume of prisms
Practise finding the surface area and volume of prisms with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

Manufacturers often use prism-shaped containers for their products. Triangular prisms and hexagonal prisms are popular choices for packaging for chocolate or cakes, for example, or for gift boxes and glasses cases.
In order to create the prism-shaped boxes, the surface area is designed with a little extra added on. This allows for tabs that are glued or fixed to hold the box or container together when it is folded up, making the complete prism shape.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Perimeter, Area, Volume
Find out more by working through a topic
- count1 of 11
- count2 of 11
- count3 of 11
- count4 of 11