Area of squares, rectangles and compound shapes - KS3 Maths

Key points

An image of a square grid. The grid has a length of thirteen squares and a width of seven squares. Two shapes have been drawn on the grid. The first shape is a one by one square. Written above: one centimetres squared. The second shape is a L shape made up of twelve squares. Each square inside the shape has been numbered. The numbers go from one to twelve. Written below: area equals twelve centimetres squared.

A shape may be a or a or, as a , it can look like two or more rectangles joined together.
For a shape drawn on a grid the may be found by counting squares. Area is measured in square units, including cm² and m².
The calculation for finding the area of a square or a rectangle is found by using a .
The total area of a compound shape is found by adding up the areas of the rectangles that have created the whole shape. This may be done in more than one way. The calculation may use a subtraction of areas where a rectangle has been removed from a larger rectangle.

Counting squares to find an area and working out the area of a square

To find the area of a rectilinear shape drawn on a grid:
- Count the squares inside the shape.
To calculate the area of a square:
- Multiply the length of one side by itself, this means the length is squared. For a whole number length, the value of the area is a .
To calculate the side length of a square:
- Find the of the area of the square.

An value for the length of one side of a square will result in an integer value for the area of a square, which is a square number. A square number is the result of multiplying an integer by itself and can be represented by a square on a grid.

Examples

Skip image gallery

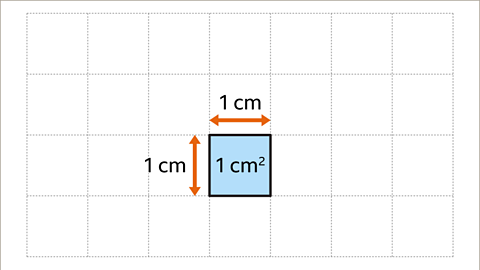
Image caption,
Area is measured in square units. On a centimetre grid each square measures 1 cm by 1 cm. Each square has an area of one square centimetre, 1 cm².
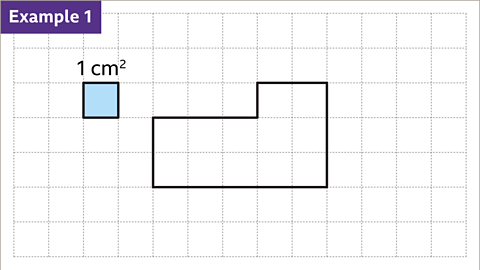
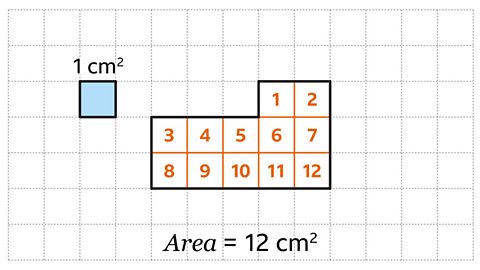
Image caption,
The rectilinear shape is drawn on a centimetre grid. Find the area of the shape.
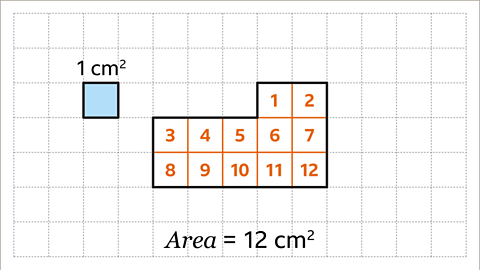
Image caption,
Count the squares inside the shape. The area of the shape is 12 cm².
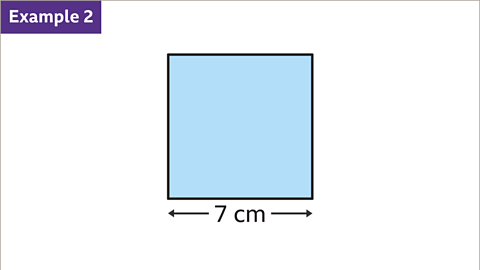
Image caption,
Find the area of a square with side-length 7 cm.
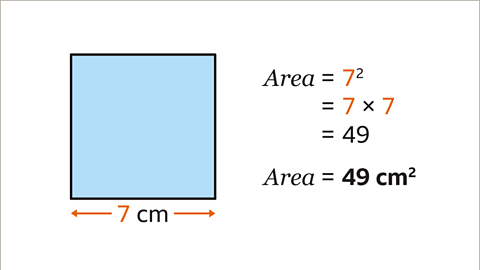
Image caption,
The area of the square is the side-length squared, 7². The side-length is multiplied by itself, 7 × 7. The area of the square is 49 cm².
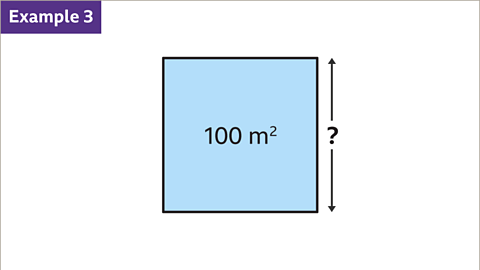
Image caption,
The area of the square is 100 m². Find the length of one side of the square.
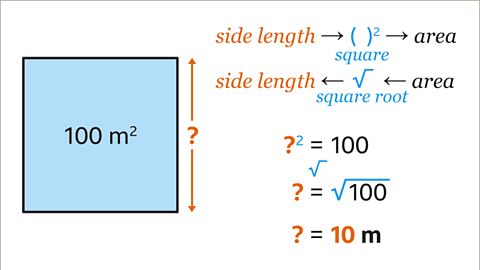
Image caption,
The area of the square is the result of squaring one side of the square. The inverse operation is to square root the area. √100 = 10. The side-length of the square is 10 m.
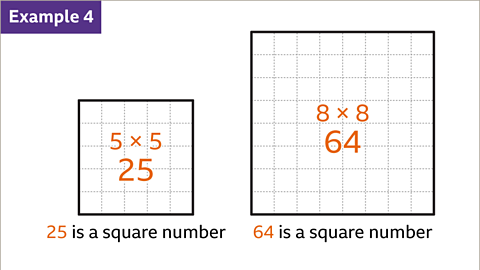
Image caption,
When a square has a whole number side-length, the numerical value of its area is a square number. An integer multiplied by itself gives a square number. 5 squared, 5² = 5 × 5, is 25. 25 is a square number. 8 squared, 8² = 8 × 8, is 64. 64 is a square number.
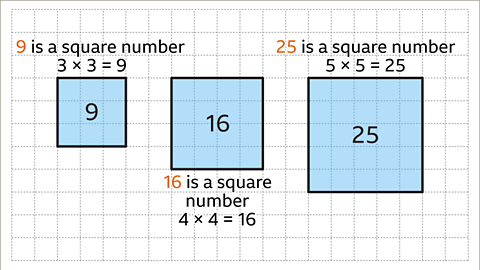
Image caption,
A square number can be shown on a grid. 9 is a square number. 9 tiles can be arranged into a 3 × 3 square. 16 is a square number. 16 tiles can be arranged into a 4 × 4 square. 25 is a square number. 25 tiles can be arranged into a 5 × 5 square.
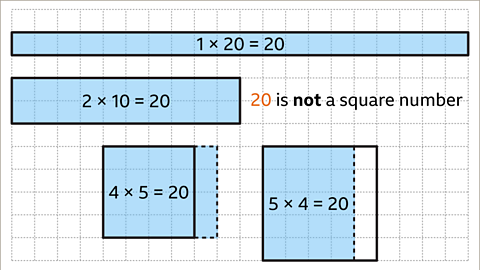
Image caption,
20 is not a square number. 20 tiles cannot be arranged into a square.

Question

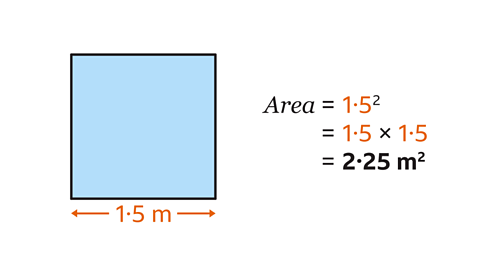
Find the area of a square with side-length 1۰5 metres.

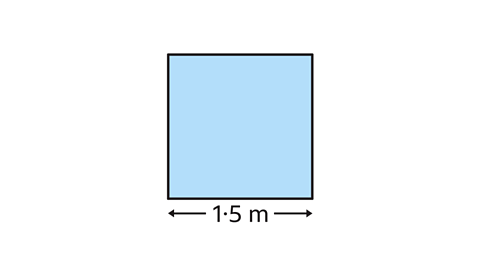
An image of a square. The length of the square has been labelled as one point five metres.

How to work out the area of a rectangle

The area of a rectangle is measured in square units including cm² and m².

To work out the area of a rectangle:
1. Check that the length and width of the rectangle are measured in the same units. If necessary, convert the units so that they match.
2. Multiply the length by the width.
3. Write the answer with the correct square units.
To work out the length or width of a rectangle:
1. Divide the given area by the given width/length.
2. Write the answer in the correct unit of length.

Examples

Skip image gallery

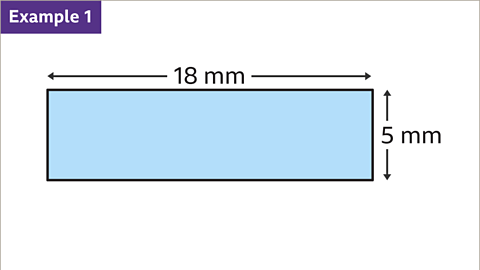
Image caption,
Find the area of a rectangle with a length of 18 mm and a width of 5 mm.
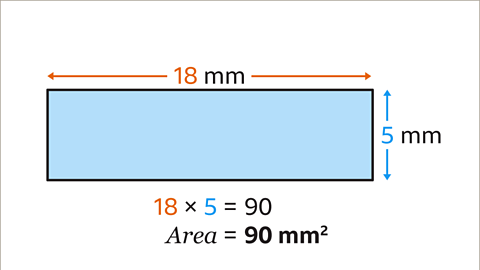
Image caption,
The length and width are measured in the same units (millimetres). Multiply the length and width. 18 × 5 = 90. The area of the rectangle is 90 mm².
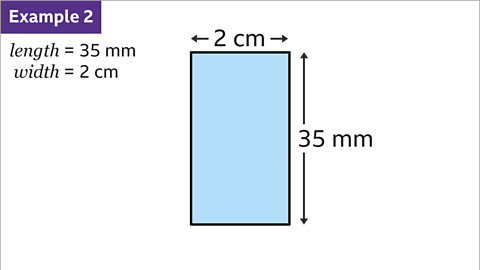
Image caption,
Find the area of a rectangle with length 35 mm and width 2 cm.
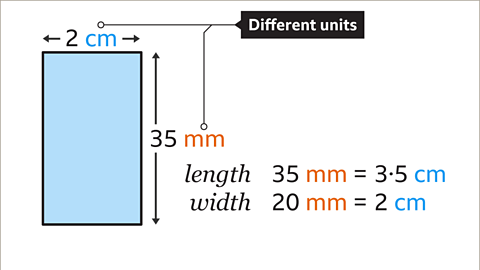
Image caption,
The length and width are not in the same units. Convert the units so that they are the same. It does not matter whether centimetres or millimetres are used, as long as the units match. 35 mm is 3۰5 cm. 2 cm is 20 mm.
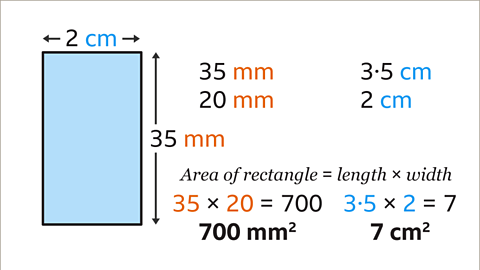
Image caption,
Multiply the length by the width. In centimetres the calculation is 3۰5 × 2. This gives an area of 7 cm². In millimetres the calculation is 35 × 20. This gives an area of 700 mm². These areas are the same. 7 cm² = 700 mm².
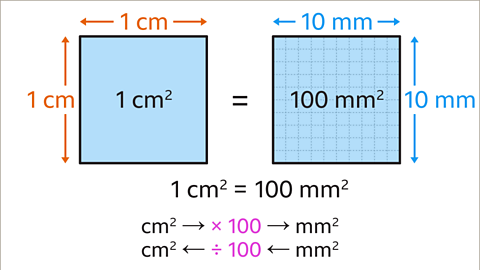
Image caption,
One centimetre is 10 millimetres. A square measuring 1 cm × 1 cm has an area of 1 cm². The same square measures 10 mm × 10 mm and has an area of 100 mm². 1 cm² is the same area as 100 mm². To convert cm² to mm² multiply by 100. To convert mm² to cm² divide by 100.
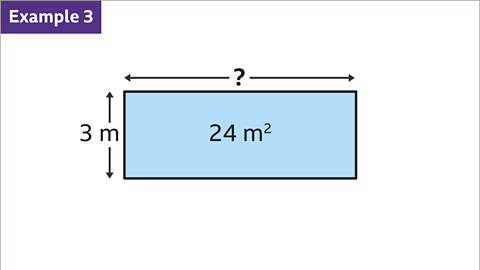
Image caption,
The rectangle has an area of 24 m² and a width of 3 m. Find the length of the rectangle.
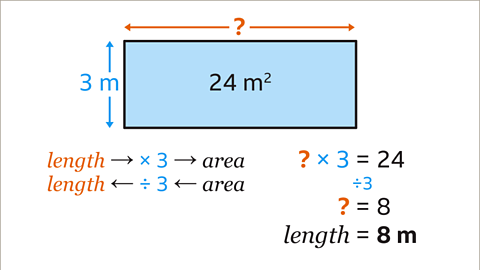
Image caption,
The area of the rectangle is the length multiplied by the width. The length has been multiplied by 3. The inverse operation of multiply by 3 is divide by 3. To work out the length of the rectangle, divide the area by the width. 24 ÷ 3 = 8. The length of the rectangle is 8 m.

Question

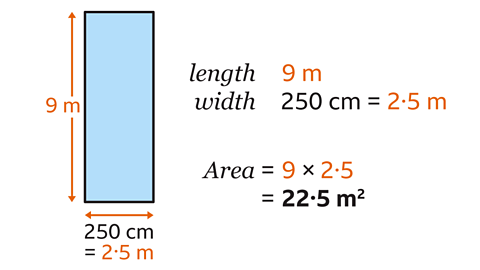
Find the area of the rectangle in square metres.

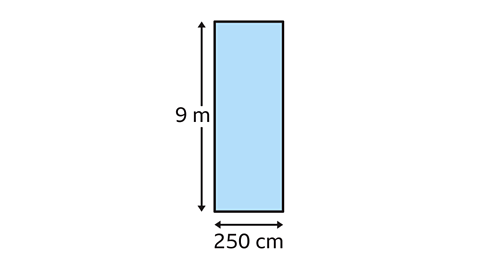
An image of a rectangle. The rectangle has length nine metres and width two hundred and fifty centimetres.

How to find the area of a compound shape

The area of a may be calculated either by adding rectangles that create the shape or by subtracting a cut-out rectangle from a larger rectangle. Sometimes there is more than one way to work out the area of a compound shape.

To find the area of a compound shape using addition:
1. Split the compound shape into rectangles that make the shape.
2. For each separate rectangle, multiply the length and width to get its area.
3. Add the separate rectangle areas to get the total area of the shape.
To find the area of a compound shape by using subtraction:
1. Identify the large rectangle and the cut-out rectangle.
2. For each rectangle, multiply the length and width to find its area.
3. Subtract the cut-out rectangle area from the large rectangle area to find the area of the compound shape.

Example

Skip image gallery

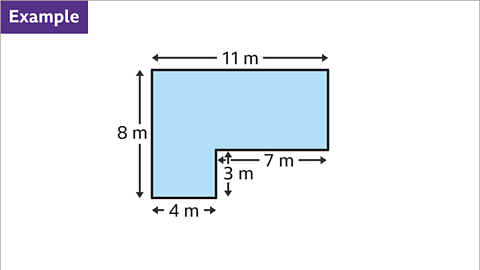
Image caption,
Find the area of the compound shape.
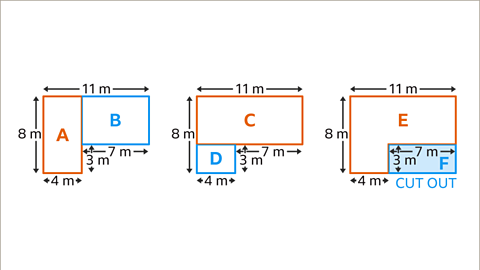
Image caption,
The area of the compound shape may be found by splitting the shape into two rectangles such as A and B or C and D, as shown in the image, and adding the two separate areas. The area can also be worked out by subtracting the smaller rectangle F from the larger rectangle E. The choice of method may depend on whether additional lengths must be worked out before the area can be calculated.
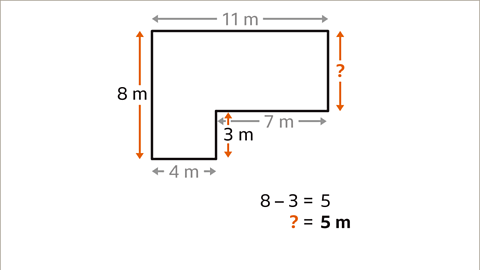
Image caption,
The shape has one missing vertical measurement. Use the other vertical measurements to find the missing value. 8 – 3 = 5. The missing measurement is 5 m. The area of the whole shape may be calculated using addition or subtraction of areas.
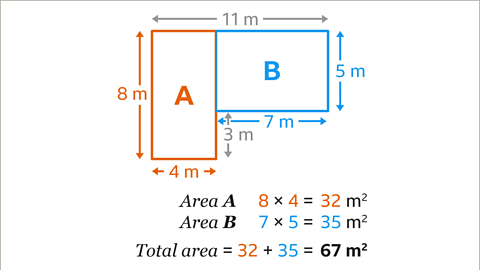
Image caption,
When the shape is split into rectangles A and B the total area can be calculated by the sum of their areas. Rectangle A measures 8 m by 4 m. The area of rectangle A is 32 m². Rectangle B measures 7 m by 5 m. The area of rectangle B is 35 m². The area of the whole shape is found by adding the area of A and the area of B. 32 + 35 = 67. The area of the whole shape is 67 m².
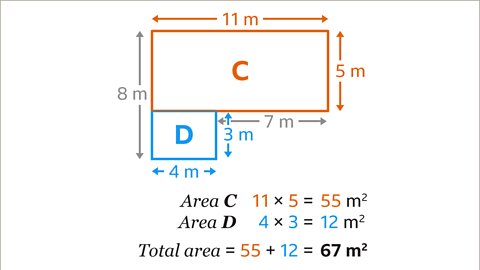
Image caption,
When the shape is split into rectangles C and D the total area can be calculated by the sum of their areas. Rectangle C measures 11 m by 5 m. The area of rectangle C is 55 m². Rectangle D measures 4 m by 3 m. The area of rectangle D is 12 m². The area of the whole shape is found by adding the area of C and the area of D. 55 + 12 = 67. The area of the whole shape is 67 m².
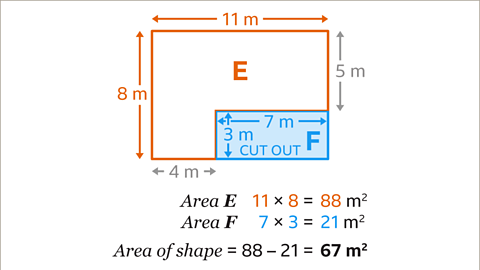
Image caption,
The area of the shape may also be found by subtracting the area of rectangle F from the area of rectangle E. Rectangle E measures 11 m by 8 m. The area of rectangle E is 88 m². Rectangle F measures 7 m by 3 m. The area of rectangle F is 21 m². The area of the compound shape is found by subtracting the area of F from the area of E. 88 – 21 = 67. The area of the shape is 67 m².

Practise finding the area of squares, rectangles and compound shapes

Quiz

Practise finding the area of squares, rectangles and compound shapes in this quiz. You may need a pen and paper to help you with your answers.

Real-life maths

An image of a piece of laminate used to cover a floor. — Image caption,
Laminate slats may come in packs that will cover 1۰8 m²

An interior designer will calculate floor area when changing the floor covering in a room. Flooring materials, including laminate slats, are sold by the square metre.

For a rectangular floor measuring 4 m by 3 m the total area would be 4 × 3 = 12 m². Laminate slats may come in packs that will cover 1۰8 m².

The number of packs needed is found by dividing the total area of the floor by the area coverage of each pack,12 ÷ 1۰8 = 6∙6

The designer will need to buy seven packs so that they have sufficient laminate slats to cover the whole floor.