Key points
A probabilityThe chance of an event happening. The probability of an event has a value from 0 to 1 and is written as a fraction, a decimal or as a percentage. The notation for the probability of an event is P(event). is how likely something is. The sumThe answer to an addition calculation of the probabilities of all the possible outcomeWhen a coin is tossed there are two possible outcomes, ‘head’ or ‘tail’. When a normal die is rolled there are six possible outcomes, 1, 2, 3, 4, 5 and 6 is 1. One of the outcomes will definitely happen.
The probability of something happening and the probability of it not happening add up to one. It is certain that an event (single)A possible outcome, for example ‘heads’ when a coin is tossed. will either happen or not happen, and that is a probability of 1.
The missing value of a probability can be worked out by subtracting the known probabilities from 1 (100% when working in percentages). The calculations may involve fractions, decimals or percentages.
When adding and subtracting probabilities to calculate unknown probability values, it is helpful to be able to add and subtract fractions and decimals.

Use the fact that the sum of probabilities of an event is 1
- To find a missing probability value:
- Add up the given probabilities.
- Subtract the total of the probabilities from 1 (100% when working in percentages).
- To add and subtract fractions, use a common denominatorA denominator that is the same for two or more fractions. .
Examples
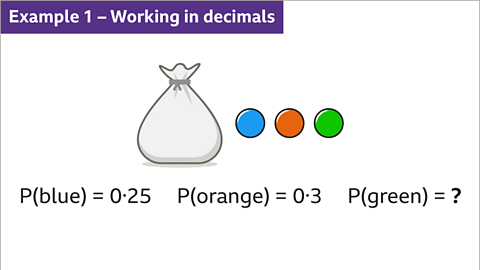
Image caption, A bag only contains blue, orange and green counters. A counter is taken at random from the bag. P(blue) = 0۰25, P(orange) = 0۰3. Work out P(green).
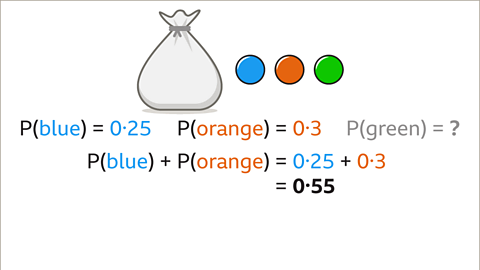
Image caption, P(green) is the sum of the known probabilities subtracted from 1. Sum the given probabilities. P(blue) + P(orange) = 0۰55
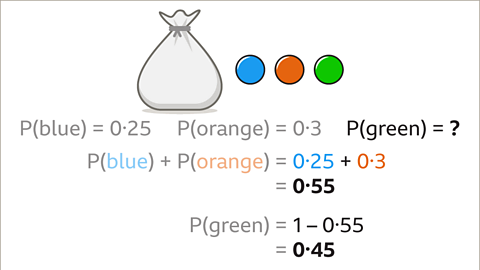
Image caption, Subtract 0۰55, the sum of the known probabilities, from 1. 1 – 0۰55 = 0۰45. P (green) = 0۰45
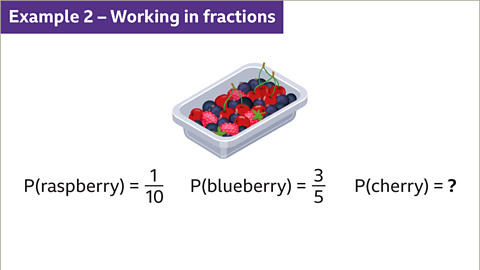
Image caption, A punnet contains raspberries, blueberries and cherries. One berry is picked out of the punnet at random. P(raspberry) = ⅒, P(blueberry) = ⅗. Find the probability of picking a cherry from the punnet, P(cherry).

Image caption, P(cherry) is the sum of the known probabilities subtracted from 1. Sum the given probabilities, P(raspberry) + P(blueberry). The highest common factor (HCF) of 5 and 10 is the common denominator used to add the fractions. The equivalent fraction for ⅗ is ⁶⁄₁₀. The fraction 1⁄₁₀ does not change, the denominator is already 10. The sum of 1⁄₁₀ and ⁶⁄₁₀ is 7⁄₁₀.

Image caption, Subtract 7⁄₁₀, the sum of the known probabilities, from 1. P(cherry) = 3⁄₁₀.
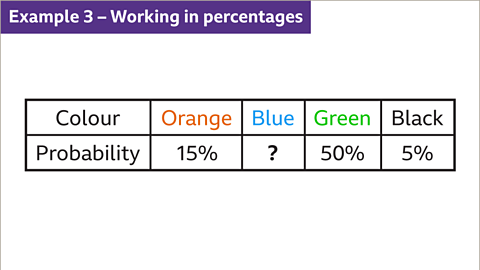
Image caption, A spinner is coloured orange, blue, green and black. The table shows the probability of a spinner landing on each colour. Find the probability of the spinner landing on blue.
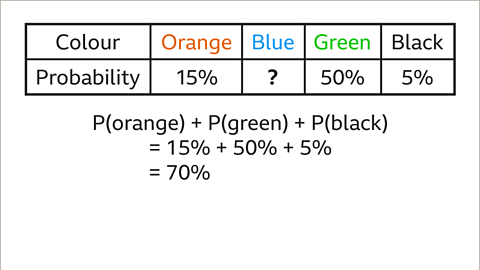
Image caption, P(blue) is the sum of the known probabilities subtracted from 100%. Sum the given probabilities. P(orange) + P(green) + P(black) = 70%.

Image caption, Subtract 70%, the sum of the known probabilities, from 100%. P(blue) = 30%.
1 of 9
Question
A raffle ticket may be purple, blue or green.
The probability of a purple ticket is \( \frac{2}{5}\).
The probability of a blue raffle ticket is \( \frac{1}{4}\).
Find the probability of a green raffle ticket.
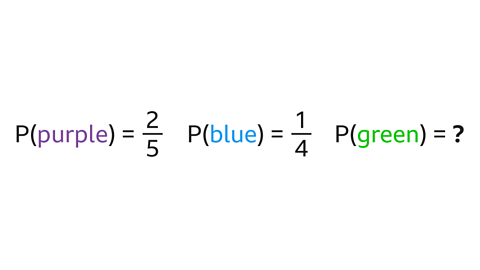
P(green) is the sum of the known probabilities subtracted from 1
Sum the given probabilities, P(purple) + P(blue). The HCF of 5 and 4 is 20
This is the common denominator used to add the fractions.
The equivalent fraction for \( \frac{2}{5} \) is \( \frac{8}{20} \).
The equivalent fraction for \( \frac{1}{4} \) is \( \frac{5}{20} \).
The sum of \( \frac{8}{20} \) and \( \frac{5}{20} \) is \( \frac{13}{20} \).
Subtract \( \frac{13}{20}\), the sum of the known probabilities, from 1
P(green) = \( \frac{7}{20} \).

Calculate the probability that an event does not happen
The probabilityThe chance of an event happening. The probability of an event has a value from 0 to 1 and is written as a fraction, a decimal or as a percentage. The notation for the probability of an event is P(event). of an event (single)A possible outcome, for example ‘heads’ when a coin is tossed. happening and the probability of the same event not happening sum to 1. It is certain that the event will either happen or not happen.
To find probability that an event does not happen.
- Subtract the P(event) from 1
The calculation may involve a fraction, decimal or percentage.
Examples

Image caption, The probability of an event happening and the probability of the same event not happening sum to 1. It is certain that the event will either happen or not happen.
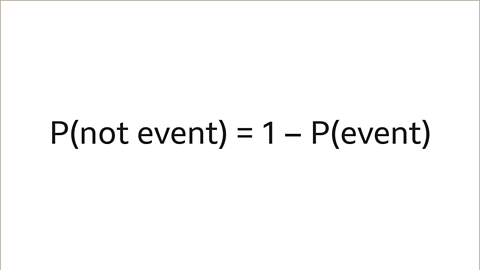
Image caption, The probability of an event not happening is the probability of the event happening subtracted from 1

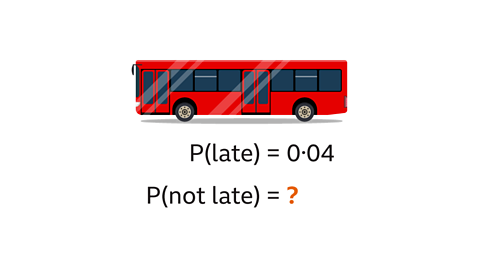
Image caption, If the probability of a bus being late is 0۰04, find the probability that the bus is not late.
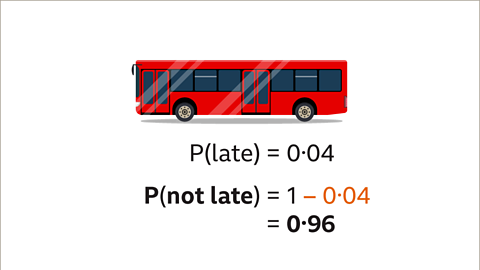
Image caption, To find the probability that the bus is not late, subtract P(late) from 1. P(not late) = 0۰96
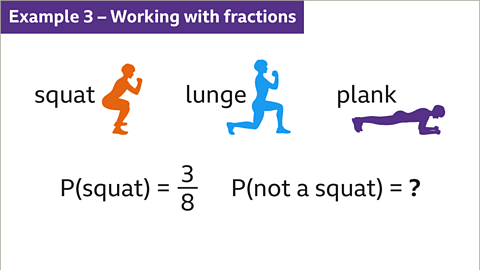
Image caption, A training session is made up of three exercises: squats, lunges and planks. The probability that the exercise is a squat is ⅜. Find the probability that the exercise is not a squat.
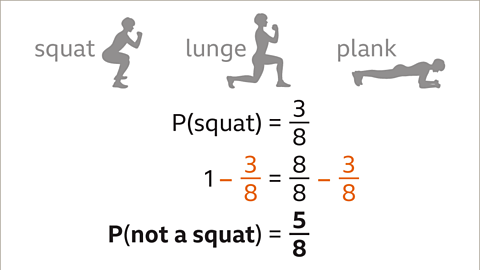
Image caption, To find the probability that the movement is not a squat, subtract P(squat) from 1. P(not a squat) = ⅝. It is not necessary to know the probability of the other movements to work this out.
1 of 6
Question
The probability that it will rain is \( \frac{1}{5}\).
What is the probability that it will not rain?
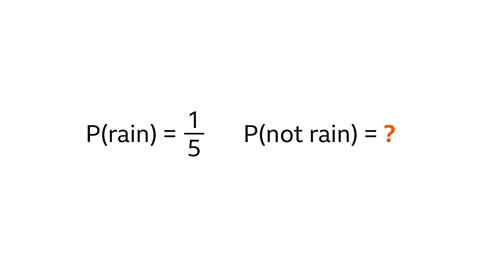
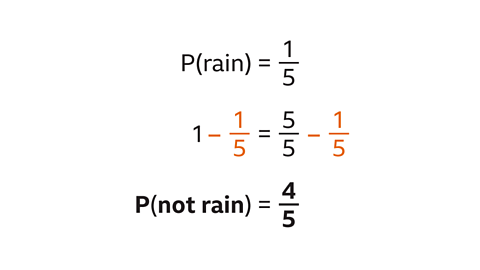
The probability that it will not rain is found by subtracting the probability that it will rain from 1
1 – \( \frac{1}{5} \) = \( \frac{4}{5} \).
P(not rain) = \( \frac{4}{5} \).
Practise finding the sum of probabilities
Practise working out the sum of probabilities with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

A meteorologist studies the weather, working with data to assess how likely it is that there will be rain, snow, wind or sun on a given day in a particular area. People use the information given by meteorologists, such as on a weather app, to make decisions when planning activities.
For example, if the probability of rain is 10%, then the probability of no rain is 90%, meaning doing something outdoors could be more appealing. If the probability of rain is 70%, this could put people off, making them decide to stay indoors instead.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Calculating probabilities
Find out more by working through a topic
- count4 of 5
- count2 of 5
