Experimental probability and relative frequency - KS3 Maths

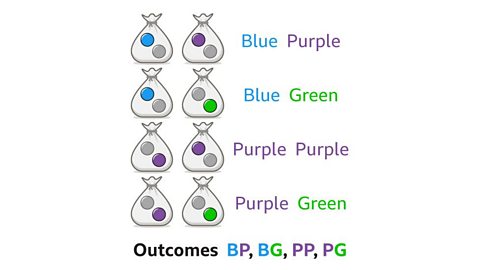
Key points

An image of a weather app being used on a mobile phone. — Image caption,
The chance of rain, shown on a weather app, is given as a percentage. This is a relative frequency, based on real data.

(experimental probability) is an estimate of worked outfrom collected data. is based on known facts.
The relative frequency is compared to the theoretical probability to decide whether a coin or a die is or . The greater the number of trials, the more reliable the data for the relative frequency.
The is calculated by multiplying the probability of an event by the number of trials.

Understanding experimental probability

Experimental probability is the relative frequency of an and is based on collected data. Theoretical probability is based on factual data.
The greater the number of trials, the more reliable the relative frequency.
The relative frequency is calculated by dividing the number of times an event happens by the total number of trials. This can have a value from 0 to 1 and may be written as a fraction or a percentage, although it is most often expressed as a decimal.
The for relative frequency is the same as for theoretical probability, P(event).

Examples

Skip image gallery

Image caption,
Relative frequency is based on collected data. This could be to do with collecting data about the weather, flipping a coin or for scientific purposes, like tagging sharks to find out where they travel to in the ocean.
Image caption,
The chance of rain, shown on a weather app, is given as a percentage. This is a relative frequency, based on real data.
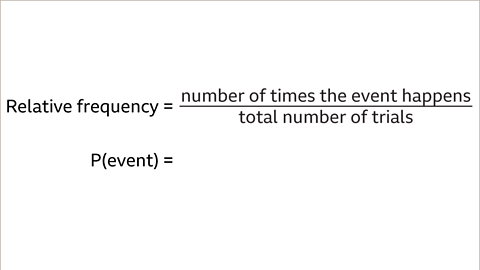
Image caption,
The relative frequency is calculated by dividing the number of times an event happens by the total number of trials. The notation is the same as theoretical probability, P(event).
Image caption,
A bag contains blue and purple counters. A counter is taken out at random, its colour recorded, then it is put back into the bag. This is done 20 times. A blue counter is taken out 14 times. Work out the relative frequency of picking out a blue counter.
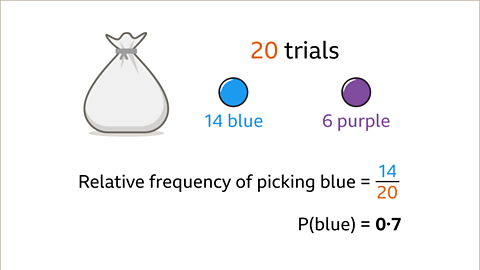
Image caption,
The relative frequency of picking a blue counter is the number of times a blue counter is picked and divided by the total number of trials, 14 ÷ 20. P(blue) = 0۰7
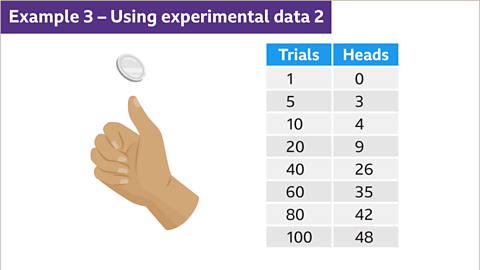
Image caption,
A fair coin is flipped. The number of heads is recorded. This data can be used to work out the relative frequency of flipping a head.
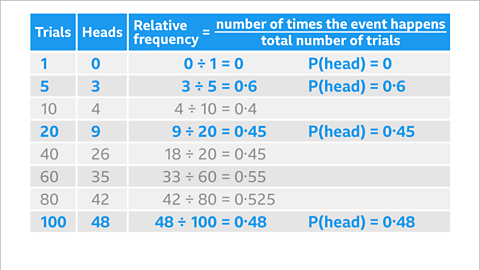
Image caption,
The relative frequency of flipping a head is calculated by dividing the number of heads by the number of trials. The relative frequency varies. One trial gives a probability of 0, P(head) = 0. After five trials, three heads show, this gives a probability of P(head) = 0۰6. After 20 trials P(head) = 0۰45. After 100 trials P(head) = 0۰48. The larger the number of trials, the more reliable the data.
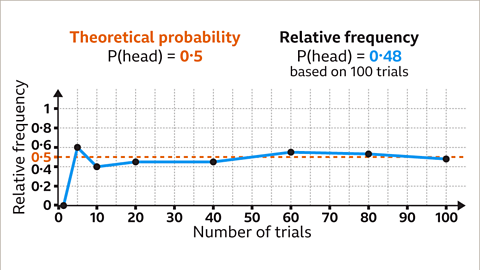
Image caption,
The theoretical probability of flipping a head with a fair coin is 0۰5. The relative frequency is based on experimental data. The more trials, the closer the relative frequency is to the theoretical probability.
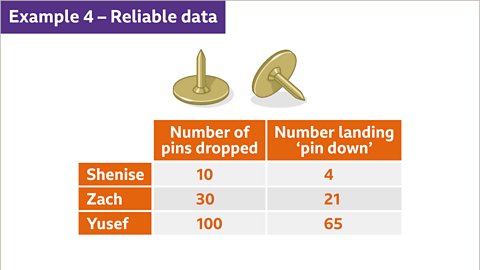
Image caption,
Shenise, Zach and Yusef drop identical drawing pins to see if they land pin up or pin down. Work out whose data gives the most reliable relative frequency.
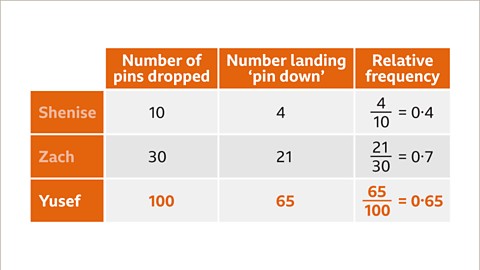
Image caption,
The relative frequency from Yusef’s data is most reliable because more pins have been dropped.

Questions

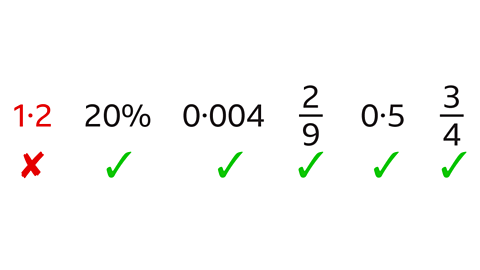
Question 1: Which of these values cannot represent a relative frequency?

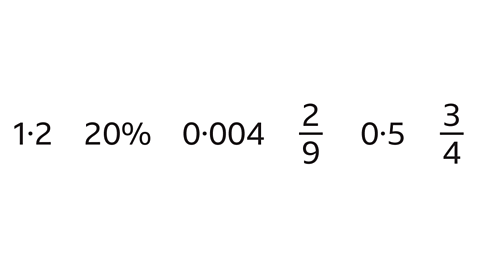
A list of numerical values: one point two, twenty percent, zero point zero zero four, two ninths, zero point five, three quarters.

Question 2: The results of flipping a coin 10 times are shown. What is the relative frequency for the coin landing on heads?

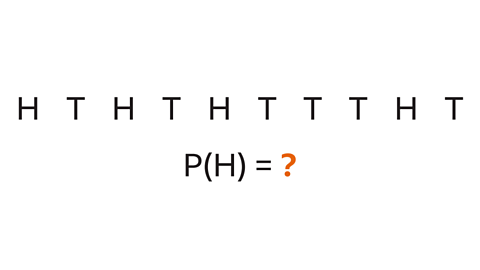
A list of ten outcomes: H, T, H, T, H, T, T, T, H, T. Written below: P, open bracket, H, close bracket, equals question mark.

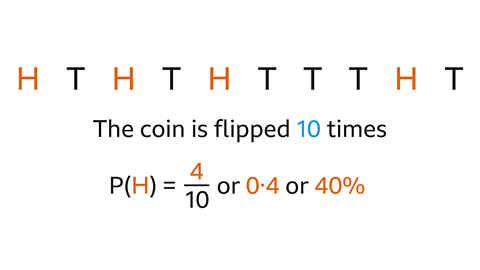
Calculating and using the expected number of outcomes

To find the number of expected outcomes:
- Multiply the probability of an by the number of trials.
To decide whether a coin or a die is :

Multiply the by the number of trials to find the expected number of outcomes.
Compare the expected number of outcomes to the actual number of outcomes.
A big difference would suggest some . The reliability of the comparison is best when there have been many trials.

To predict an expected number of outcomes for a future event:
- Multiply the of the event by the number of trials.

Examples

Skip image gallery

Image caption,
The expected number of outcomes of a particular event is calculated by multiplying the probability of that event by the number of trials.
Image caption,
The probability that a flower will grow from a seed is 80%. There are 200 seeds in a packet. Work out how many flowers are expected to grow.
Image caption,
The expected number of flowers that will grow is worked out by multiplying the probability that a flower will grow by the number of trials, represented by the number of seeds in the packet. 80% × 200 is 80% of 200. The expected number of flowers that will grow from the packet of 200 seeds is 160
Image caption,
A coin is flipped 10 times. There are 3 heads and 7 tails. Work out whether the coin is biased or not.
Image caption,
A fair coin has two equally likely outcomes, heads or tails. Each outcome has a probability of 0۰5, a half. The probability multiplied by the number of flips is 0۰5 × 10. This gives 5 expected heads and 5 expected tails. This is less than 7, so it seems that the coin is biased. However, the coin has only been flipped 10 times. A small number of trials does not give reliable data, so it is not possible to state whether the coin is biased or fair.
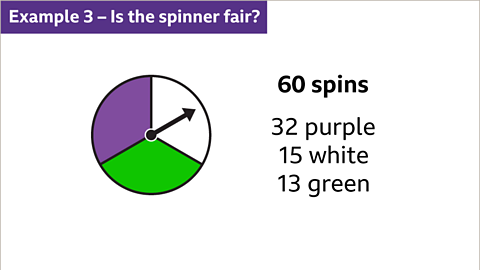
Image caption,
A spinner can land on purple, white or green. The results after 60 spins are 32 purple, 15 white and 13 green. Decide whether the spinner is fair or not.
Image caption,
For a fair spinner the probability of purple, green and white will be the same, ⅓. The expected number of outcomes of each colour is the probability multiplied by the number of trials. ⅓ × 60 = 20. The spinner lands on purple 32 times. This is over half of the spins. The spinner lands on white for a quarter of the spins and a little less than a quarter of the spins on green. There have been a lot of spins, so it is reasonable to say that the spinner is biased. It is biased to show purple about half the time and green and white about a quarter of the time. More trials will increase the reliability of the decision.
Image caption,
A spinner can land on green or blue. After 400 spins the relative frequency of green is 0۰35. Work out the number of times the spinner landed on blue.
Image caption,
The number of times the spinner lands on green is calculated by multiplying the relative frequency of green by the number of spins. 0۰35 × 400 = 140. The spinner lands on green 140 times. The spinner can only land on green or blue. The rest of the spins are blue. 400 – 140 = 260. The spinner lands on blue 260 times.
Image caption,
The relative frequency of green and the relative frequency of blue sum to 1. The relative frequency of blue is 1 – 0۰35 = 0۰65. The number of times the spinner lands on blue is calculated by multiplying the relative frequency of blue by the number of spins, 0۰65 × 400 = 260. The spinner lands on blue 260 times.

Question

The relative frequency of a hockey player scoring from a penalty is 0۰8

How many goals are expected from 15 penalties?

Relative frequency of scoring from a penalty equals zero point eight. Written below: fifteen penalties.

Practise working out experimental probability and relative frequency

Practise working out experimental probability and relative frequency with this quiz. You may need a pen and paper to help you with your answers.

Quiz

Real-life maths

An image of a marine biologist. They are weighing the mass of a sample of small fish. — Image caption,
A marine biologist tags and records fish before returning them to the lake.

A studying the fish in a lake may use relative frequency in a process called capture-recapture which helps them to estimate the total number (𝑵) of fish in the lake.

This method works by assuming that each fish has an equal chance of being captured. For example, a sample of 80 fish could be taken, which are all then tagged. Later a second sample of 30 fish is taken and the number of them that are tagged is recorded. In this case, two of the fish are tagged.

The relative frequency of picking a tagged fish is \( \frac{2}{30} \), which is the same as the original \( \frac{80}{𝑵} \).

To find the population of fish in the lake the formula 𝑵 = \( \frac{(80×30)}{2} \) is used. The number of fish in the lake is estimated to be 1200

This technique is used to estimate animal populations as well as in studies of human populations. It can help to produce more accurate information relating to rates of disease and other health conditions.