Key points
- probabilityThe chance of an event happening. The probability of an event has a value from 0 to 1 and is written as a fraction, a decimal or as a percentage. The notation for the probability of an event is P(event). is the chance of an event happening. It is expressed as a value on a scale from 0 to 1. It can be written as a fraction, a decimal or a percentage.
- Where an event (single)A possible outcome, for example ‘heads’ when a coin is tossed. is impossible, its probability is 0 and where it is certain its probability is 1. This can be presented visually on a probability scaleThis is a scale between 0 (zero) and 1. 0 means the event is impossible. 1 means the event is certain. .
- A probability scale allows the probability of events to be placed in order of likelihoodThe chance that a particular outcome will occur.. The probabilities marked on the probability scale may be used to make statements comparing different outcomes.
- The vocabulary used in probability includes impossible, unlikely, even chance, likely and certain. These descriptions can help order the likelihood of a set of events.

Describing probabilities
- The probability (chance) of something happening can be described using particular words:
Certain
Very likely
Likely
Even chance
Unlikely
Very unlikely
Impossible
The notationAn agreed form of presentation for mathematical information. for writing the probability of an event is P(event).
The sample spaceThe sample space is the set of all possible outcomes. For a single event this can be a list of outcomes, written in set notation S = {…….}. For combined events this is usually presented in a table. The sum of all the probabilities for all the events in a sample space is 1. is the set of all possible outcomes. This can be written as a list, S = {……}.
- For example if a fair coin is tossed the possible outcomeA potential result. When a coin is tossed there are two possible outcomes ‘head’ or ‘tail’. When a normal die is rolled there are six possible outcomes, 1, 2, 3, 4, 5 and 6. are {H, T} for heads or tails. The probability of getting a head is written as P(H).
The greater the proportion of times an event can happen the greater (or more likely) the probability. Events can be ordered by the probability of them happening (how likely each event is).
Examples
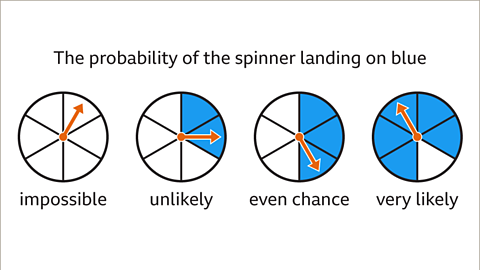
Image caption, The probability of the spinner landing on blue can be described in words.
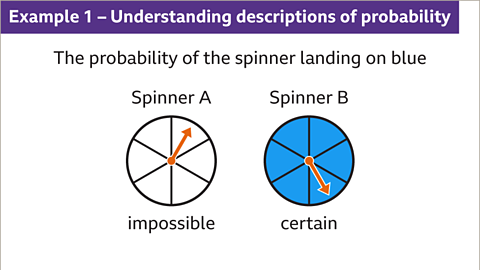
Image caption, The probability of the spinner landing on blue on spinner A is described as impossible because there are no blue sectors. The spinner cannot land on blue. The probability of the spinner landing on blue on spinner B is described as certain because all the sectors are blue. The spinner must land on blue.
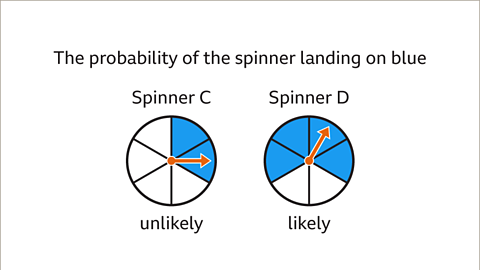
Image caption, The probability of the spinner landing on blue on spinner C is described as unlikely because there are fewer blue sectors than white sectors. The probability of the spinner landing on blue on spinner D is described as likely because there are more blue than white sectors.
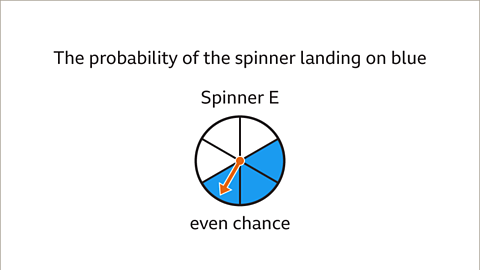
Image caption, The probability of the spinner landing on blue on spinner E is described as an even chance because there are an equal number of blue and white sectors. The probability of landing on blue is equal to the probability of landing on white.
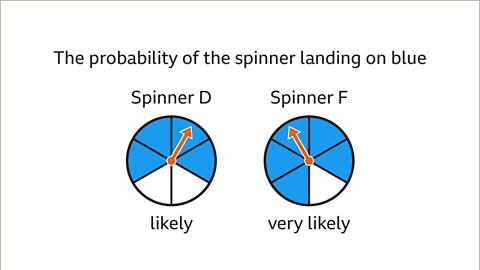
Image caption, The probability of the spinner landing on blue on spinner D is described as likely. There are more blue than white sectors. The probability of the spinner landing on blue on spinner F is described as very likely. There are even more blue sectors on spinner F than on spinner D.

Image caption, P(event) is the convention for writing ‘the probability of an event’. P(blue) means ‘the probability that the outcome is blue’. S = {…} is the sample space, listing the possible outcomes. Where the spinners can show blue or white there are two outcomes in the sample space. There is no indication of how likely the outcomes are.

Image caption, Order these events by their probability, from least likely to most likely: rolling an odd number, rolling a number less than 3, rolling a 3, rolling a number greater than 6, and rolling a number less than 7

Image caption, A fair die is rolled. The sample space is the numbers 1, 2, 3, 4, 5 and 6. These are all the possible outcomes. The probability of each event can be described in words: Impossible – Very unlikely – Unlikely – Even chance – Likely – Very likely – Certain.

Image caption, P(odd) has an even chance because there are an equal number of odd and even numbers. P(< 3) is unlikely because only two of the six numbers are less than 3. P(3) is very unlikely as only one of the six numbers is a three. P(> 6) is impossible because none of the numbers on a die are greater than 6. P(< 7) is certain because all of the numbers on a die are less than 7. The probabilities of the events can now be ordered.
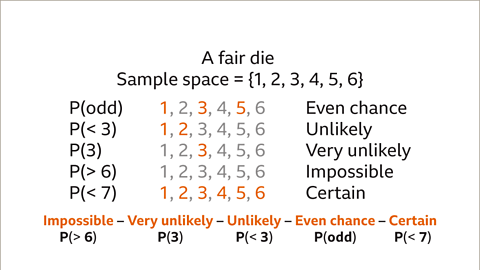
Image caption, In order of likelihood, from impossible to certain, the probabilities are P(> 6), P(3), P(< 3), P(odd) and P(< 7).
1 of 10
Practise sample spaces and outcomes
Practise describing different probabilities with this quick quiz.
Understanding the probability scale
The probability scale can be labelled in fractions, decimals or percentages.
The scale goes from 0 to 1 (0% to 100%):
- An impossibleevent (single)A possible outcome, for example ‘heads’ when a coin is tossed. has a probability of zero (0%)
- A certain event has a probability of 1 (100%)
- Other events have probabilities between 0 and 1
The probabilities of events can be compared using their positions on the probability scaleThis is a scale between 0 (zero) and 1. 0 means the event is impossible. 1 means the event is certain. .
The probability scale can be subdivided into equal intervals to show other probabilities:
- For example, four intervals labelled from 0 to 1 with subdivisions marked ¼ and ½ and ¾. This is the same as 0% and 100% with subdivisions marked 25%, 50%, and 75%.
Examples
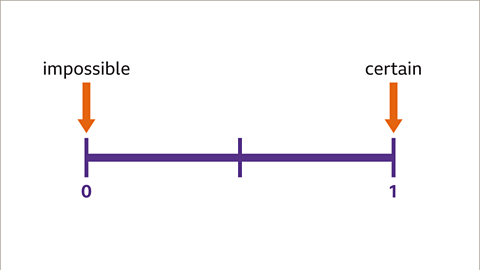
Image caption, The probability scale is labelled from 0 to 1. An impossible event has a probability of 0. A certain event has a probability of 1. Other events have probabilities between 0 and 1
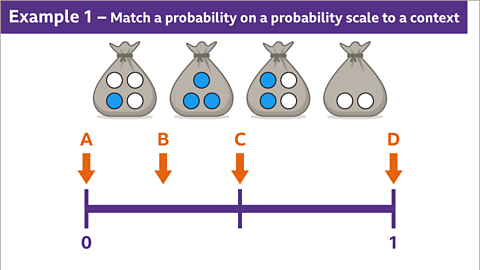
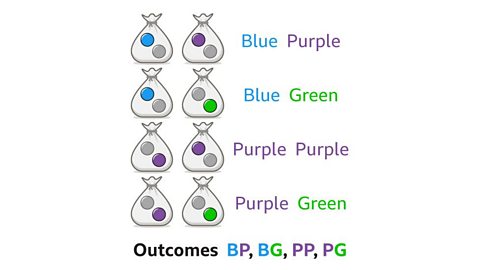
Image caption, The probabilities of events can be compared using their positions on the probability scale. Each letter represents the probability of taking a blue ball at random from one of the bags.
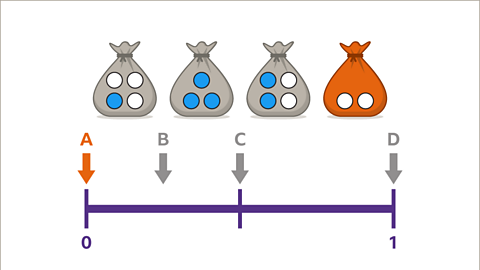
Image caption, Event A shows that the probability of taking a blue ball at random from a bag is zero. It is impossible. The bag on the far right has no blue balls. P(Blue) = 0
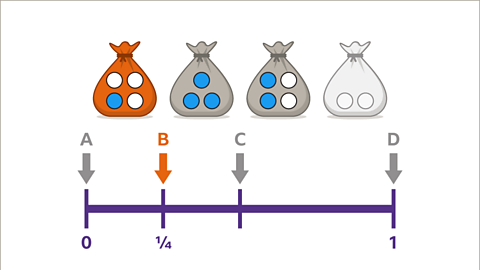
Image caption, Event B shows that the probability of taking a blue ball at random from a bag is ¼ (25%). This means that a quarter of the balls in the bag are blue. This is true for the bag on the far left, one of the four balls is blue. P(Blue) = ¼.
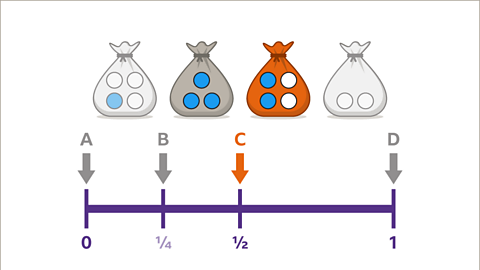
Image caption, Event C shows that the probability of taking a blue ball at random from a bag is ½ (50%). This means that half of the balls in the bag are blue. This is true for the bag that contains two blue and two white balls, half the balls are blue. P(Blue) = ½.
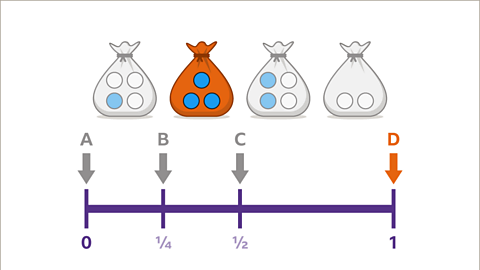
Image caption, Event D shows that the probability of taking a blue ball at random from a bag is 1 (100%). This means that the probability of picking a blue ball is certain. This is true for the bag that contains only blue balls. All the balls are blue. P(Blue) = 1
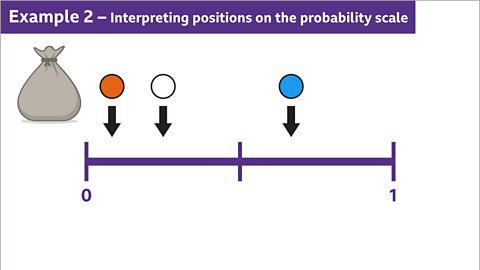
Image caption, A bag contains counters. The counters are orange, white, or blue. The probability of taking a counter of a particular colour from the bag is shown on the probability scale. Statements can be made based on this information.
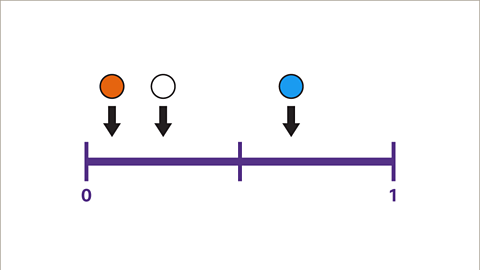
Image caption, The probability of taking a blue counter out of the bag is greater than the probability of taking a white counter. There are more blue counters than white counters in the bag. The number of counters is not known.
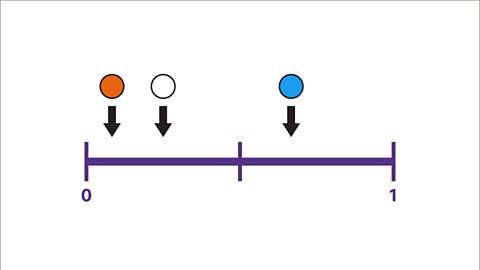
Image caption, The probability of taking a white counter out of the bag is greater than the probability of taking an orange counter. There are more white counters than orange counters in the bag. The number of counters is not known.
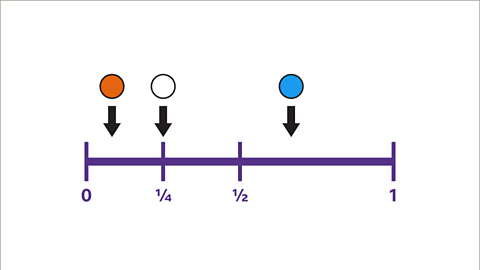
Image caption, The probability of a blue counter is greater than ½, this means that more than half of the counters are blue. The probability of a white counter is ¼, this means that a quarter of the counters are white. There is not enough information to decide how many of each coloured counter is in the bag.
1 of 10
Question
A box of chocolates contains toffees and fudges. The probability scale shows the probability of taking a toffee from the box.
Decide if each statement below is true or false or if there is not enough information to tell.
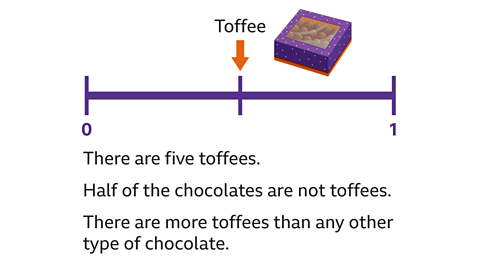
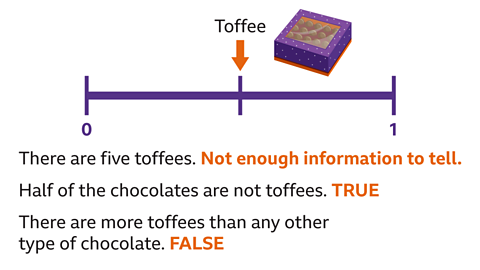
The probability scale shows that there is an even chance (50%, ½) of picking a toffee. Half of the chocolates are toffees. There are only toffees and fudges in the box so if half are toffees, half are fudges.
There are five toffees.
There is not enough information to tell. The number of chocolates in the box is not given. There will only be five toffees in the box if there are ten chocolates in total.
Half of the chocolates are not toffees.
True. They are either toffees or fudges. Half are toffees, so half are not toffees.
There are more toffees than any other type of chocolate.
False. There are equal amounts of toffees and fudges so there cannot be more toffees than another type of chocolate.
Practise describing probabilities
Practise describing probability and using the probability scale with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

Charities often raise money by having raffles. In a raffle, tickets are selected by lucky-dip. Usually, tickets that end in a zero or a five win a prize, which means one ticket in every five will win a prize.
Charities need to calculate how many tickets they need to sell and how much prizes cost in order to make a profit for the charity. Even though the chance of winning is unlikely, raising money for charity and the bonus of a possible prize makes it worthwhile.
Other raffle ticket prizes may be selected during the event and are not based on the ticket number. The chance of winning one of these prizes is less as there are fewer prizes for more tickets.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Calculating probabilities
Find out more by working through a topic
- count2 of 5

- count3 of 5
- count4 of 5