How to work out the probability of an event

Key points

An image of a die. Written above: Roll a six sided die. Written below: Outcomes: one, comma, two, comma, three, comma, four, comma, five, comma, six. The outcomes are coloured orange. — Image caption,
The outcomes of rolling a six-sided die are: 1, 2, 3, 4, 5, 6.

Listing all possible outcomes of an event can be used to work out probabilities. The of an event can be written as a fraction where the is the number of outcomes where the event happens, and the is the total number of outcomes.
Probabilities can also be presented on a .
A probability of zero means an outcome is impossible. A probability of 1 means an outcome is certain. All other probabilities have a value between 0 and 1.
are equally likely when they have the same probability.
- A coin is equally likely to land on heads or on tails.
- A fair six-sided is equally likely to land on 1, 2, 3, 4, 5 or 6.
- A spinner that has half its sectors coloured blue and the other half white, is equally likely to stop on blue or on white.
Knowing about number facts, including recognising factors, multiples, prime numbers and square numbers, is useful when working through probability questions.

Listing outcomes

Listing outcomes means writing down all the possible outcomes of an event.
An could be the result of:
- rolling a standard six-sided die
- flipping a fair coin
- taking a counter at random out of a bag
- twirling a coloured spinner
When there is one of each outcome, usually the outcomes are equally likely. If there are more of one outcome than another, the outcomes are not equally likely.

Examples

Skip image gallery

Image caption,
List all the possible outcomes for rolling a fair standard six-sided die.
Image caption,
For a standard six-sided die the outcomes are the numbers 1, 2, 3, 4, 5 and 6. Each of these outcomes is equally likely. Each outcome has the same probability of happening.
Image caption,
List all the possible outcomes when a fair coin is flipped.
Image caption,
For a fair coin there are two equally likely outcomes: heads, or tails.
Image caption,
List all the possible outcomes when a counter is taken at random from the bag.
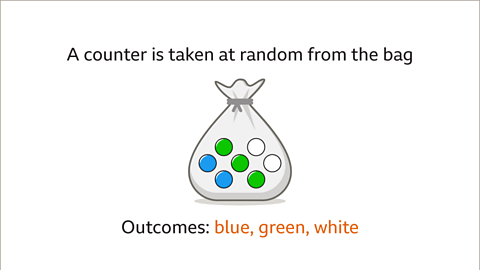
Image caption,
The possible outcomes when taking a counter out of the bag are a counter that is coloured blue, green or white. The outcomes are not equally likely because there are more green counters in the bag. The probability of taking a blue counter is the same as the probability of taking a white counter because there are equal amounts of the blue and white counters.
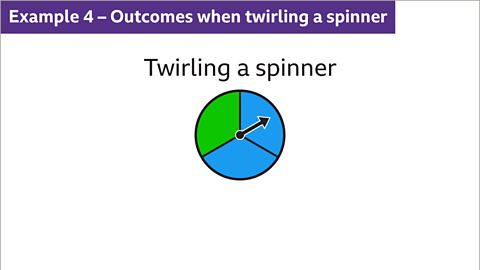
Image caption,
List all the possible outcomes of twirling the spinner.
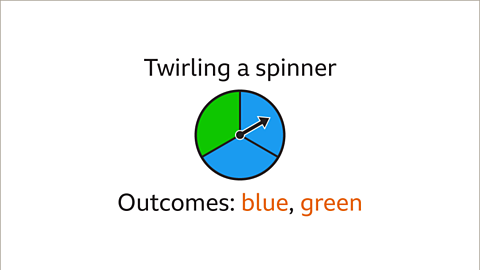
Image caption,
The spinner may land on blue or green. The outcomes are not equally likely because there are more blue sectors than green sectors. The spinner is twice as likely to land on blue as it is to land on green.
Image caption,
List all the possible outcomes of a football match.
Image caption,
There are three possible outcomes for a football match: win, lose or draw. They are not equally likely. The probability of each outcome will depend on the players in a team, their opposition, and maybe other factors too.

Question

Five lettered tiles that spell the word ALPHA are put into a bag. One tile is taken at random from the bag.

List all the possible outcomes.

8An image of a bag with lettered tiles inside. The bag has five tiles: two letter a’s, one letter l, one letter p, and one letter h. Drawn above: the same five lettered tiles spelling the word: alpha. The tiles are coloured blue.

Finding the probability of an event

The of an can be written as a fraction:
- the numerator is the number of outcomes where the event happens
- the denominator is the total number of outcomes
The probability may also be represented on a .

Number facts, including recognising factors, multiples, prime numbers and square numbers, often appear in probability questions.

Examples

Skip image gallery

Image caption,
Rolling a fair die has six equally likely outcomes: 1, 2, 3, 4, 5 and 6. Find the probability of the listed events as a fraction and show them on the probability scale.
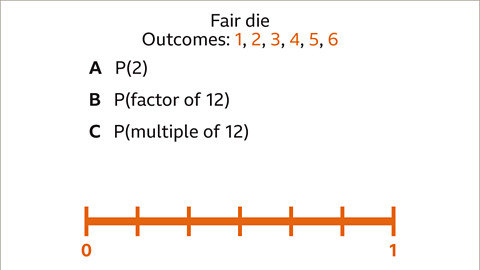
Image caption,
There are six equally likely outcomes. The probability scale is marked with six intervals, giving steps of one sixth.
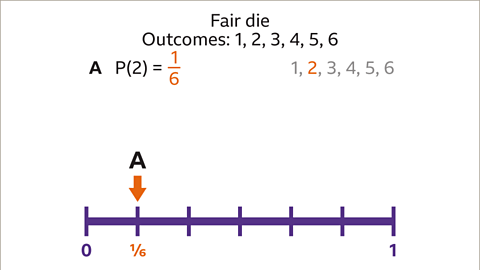
Image caption,
Rolling a fair die has six equally likely outcomes. Each outcome is equally likely. The probability of rolling a 2 is one sixth because one outcome out of the six possible outcomes is a 2. P(2) = 1⁄6, which can be shown on the probability scale with an arrow pointing to 1⁄6.
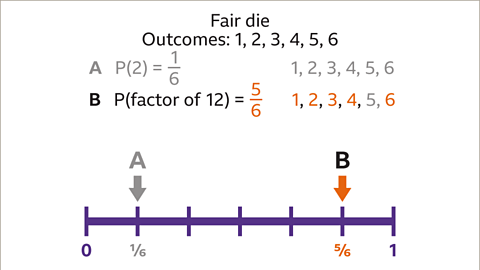
Image caption,
The probability of rolling a factor of 12 is five sixths because five out of the six possible outcomes is a factor of twelve. 1, 2, 3, 4 and 6 are all factors of 12. P(factor of 12) = ⅚. This can be shown on the probability scale with an arrow pointing to ⅚.
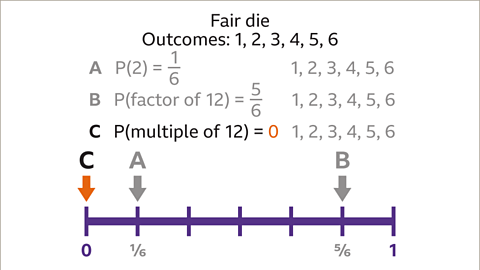
Image caption,
The probability of rolling a multiple of 12 is zero because none of the six possible outcomes is a multiple of 12. This can be shown on the probability scale, with an arrow pointing to 0
Image caption,
What is the probability of the spinner landing on blue?
Image caption,
The spinner has three equal sectors. Two of the sectors are coloured blue and one is coloured green. The probability of the spinner landing on blue is written as the fraction ⅔.
Image caption,
What is the probability of taking a green counter from the bag?
Image caption,
There are seven counters in the bag. Three of the counters are green. The probability of taking a green counter from the bag is written as the fraction ³⁄₇.

Question

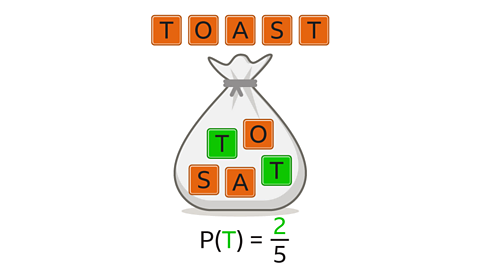
Five lettered tiles that spell the word TOAST are put into a bag. One tile is taken at random from the bag.

What is the probability that a letter T is taken out of the bag?

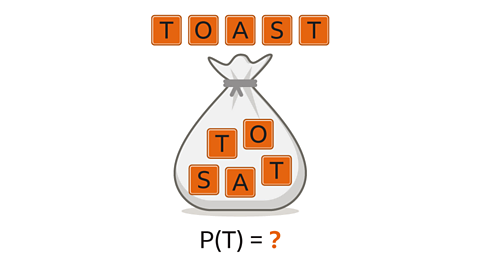
An image of a bag with lettered tiles inside. The bag has five tiles: two letter t’s, one letter o, one letter a, and one letter s. Drawn above: the same five lettered tiles spelling the word: toast. The tiles are coloured orange.

Practise finding probabilities

Practise finding probabilities with this quiz. You may need a pen and paper to help you with your answers.

Quiz

Real-life maths

An image of a referee, flipping a coin, between two captains from opposing teams. — Image caption,
Flipping a coin before a sports match is fair as there are only two possible outcomes.

An unbiased coin is usually flipped at the start of a sports match. This decides which team or player starts and the direction they want to play in first, or whether to be the first to serve or bat.

It is a fair method of choosing as the coin has two equally likely outcomes: heads or tails.