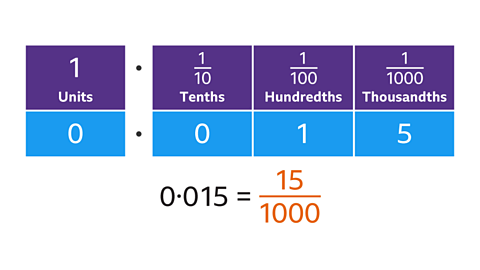
Key points
- Fractions can be subtracted when they have the same denominatorNumber written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1⁄3, the denominator is 3. The differenceThe numerical difference between two numbers is found by comparing the quantities. A difference is always a positive value. The difference between 3 and 5 is 2, the difference between 5 and 3 is 2 is found by subtracting the numeratorNumber written at the top of a fraction. The numerator is the number of parts used. Eg, for 1⁄3, the numerator is 1.
- When fractions have different denominators, they are converted to equivalent fractionA fraction with the same value as another.. The denominators are changed to the lowest common multiple (LCM)The lowest multiple that is common to two or more numbers. The LCM of 15 and 12 is 60 because it is the lowest value in both of their multiplication tables. Also known as the least common multiple. they share, making them the same.
- improper fractionA fraction where the numerator is greater than the denominator, eg 9⁄4 can be subtracted as they are.
- To find the difference between mixed numberA number that is written using a whole number and a fraction, eg 3 4⁄5, change the mixed numbers to improper fractions first and then do the subtraction.
- To find the difference between mixed numbers where the second fractional part is less than the first fractional part, subtract the integerIntegers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, 8, and 10000 are examples of integers. parts and fractional parts separately.
Subtracting fractions with the same denominator
To find the difference between fractions with the same denominator, subtract the numerators. The denominator remains the same.
To subtract mixed numbers with the same denominators:
Subtract the integers and subtract the fractions.
When the fraction to be subtracted is bigger than the first fraction, change the mixed numbers to improper fractions first then do the subtraction.
The answer can be left as an improper fraction or changed to a mixed number if required.
Examples
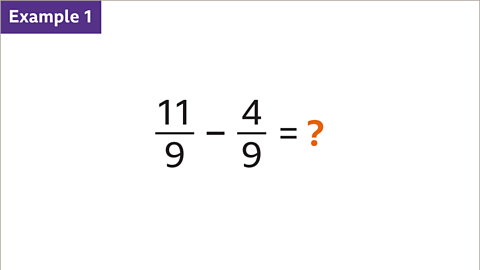
Image caption, Subtract 4⁄9 from 11⁄9
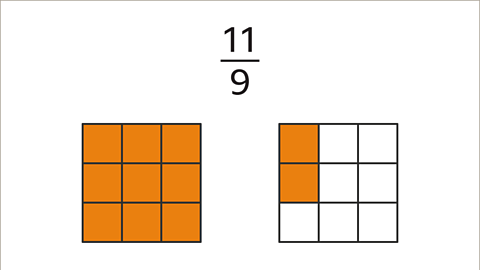
Image caption, 11⁄9 is shown in this model.
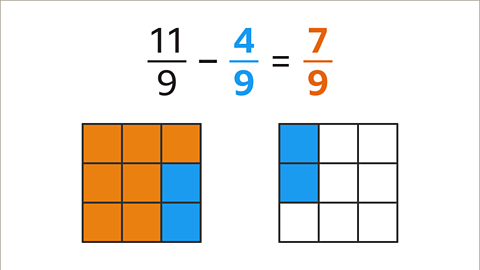
Image caption, The denominators are the same, so subtract the numerators. Calculate 11 – 4. The answer is 7⁄9
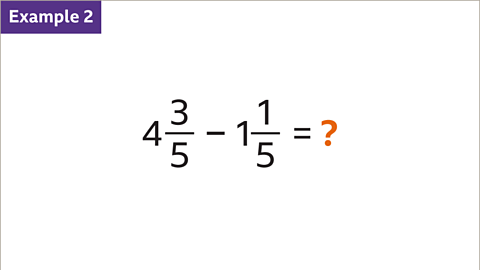
Image caption, Subtract 1 1⁄5 from 4 3⁄5
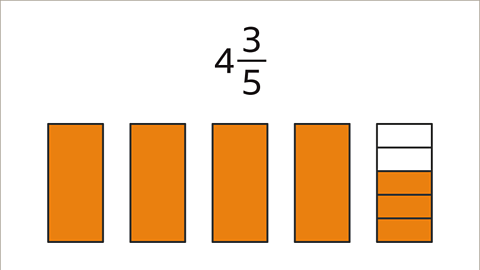
Image caption, 4 3⁄5 is a mixed number. It is shown in this model.
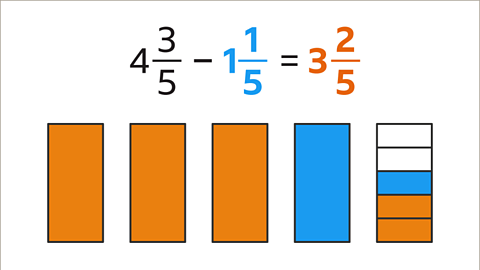
Image caption, Subtract the integers (4 – 1 = 3). Subtract the fractions by subtracting the numerators (3⁄5 – 1⁄5 = 2⁄5). 4 3⁄5 – 1 1⁄5 = 3 2⁄5
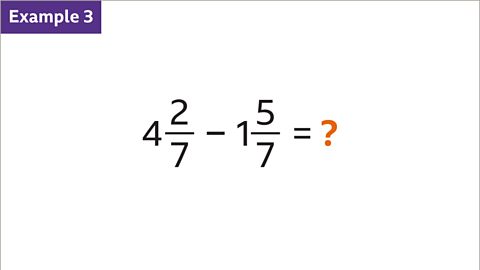
Image caption, Find the difference between 4 2⁄7 and 1 5⁄7
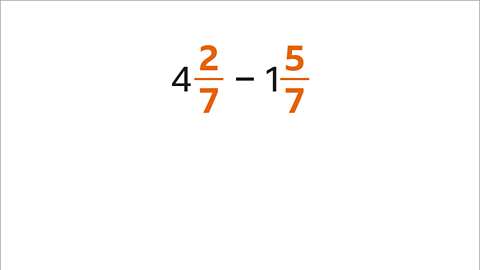
Image caption, The fraction to be subtracted (5⁄7) is bigger than the first fraction (2⁄7). The most efficient method for a calculation like this is to change the mixed numbers to improper fractions first.
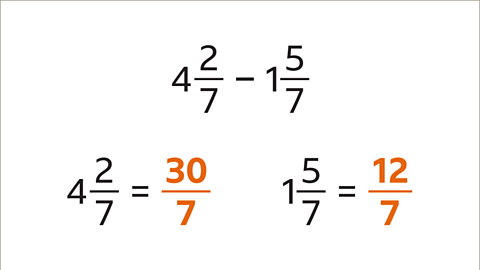
Image caption, The mixed numbers have been changed to improper fractions.
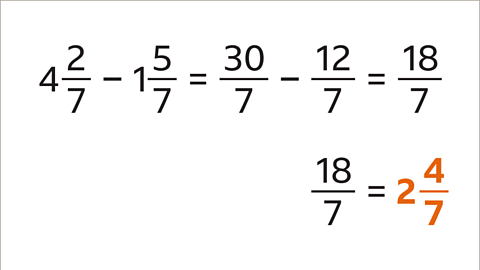
Image caption, The subtraction can now be calculated: 30⁄7 – 12⁄7 = 18⁄7. The answer could be left as an improper fraction, or written as a mixed number if required: 18⁄7 = 2 4⁄7
1 of 10
Question
Calculate \( \frac{5}{7} - \frac{3}{7} \)
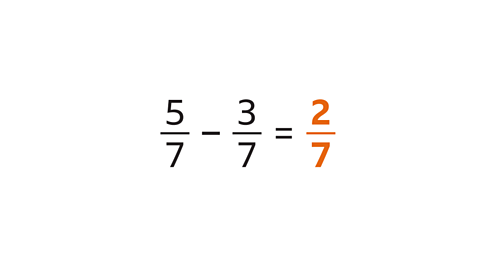
The denominators are the same. Subtract the numerators.
\( 5 – 3 = 2 \)
\( \frac{5}{7} - \frac{3}{7} = \frac{2}{7} \)
Subtracting fractions with different denominators
To subtract fractions with different denominators:
Find the lowest common multiple (LCM)The lowest multiple that is common to two or more numbers. The LCM of 15 and 12 is 60 because it is the lowest value in both of their multiplication tables. Also known as the least common multiple. of the denominators.
Rewrite the fractions as equivalent fractionA fraction with the same value as another. with the same denominator.
Complete the subtraction.
To subtract mixed numbers with different denominators:
Subtract the integerIntegers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, 8, and 10000 are examples of integers..
Subtract the fractions using equivalent fractions with the same denominator.
To subtract mixed numbers with different denominators, when the second fraction is greater than the first fraction:
Change the mixed numbers to improper fractions.
Do the subtraction.
The answer can be left as an improper fraction or changed to a mixed number if required.
Examples
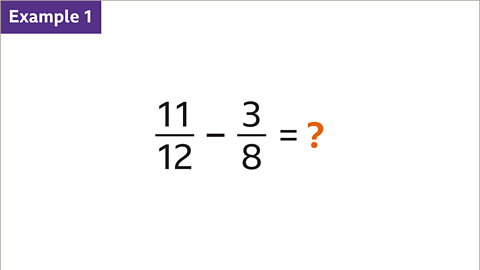
Image caption, Work out 11⁄12 minus 3⁄8
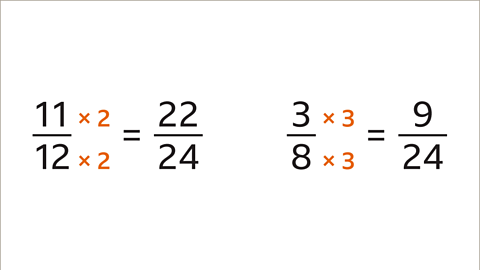
Image caption, The LCM of 12 and 8 is 24. Write equivalent fractions with a denominator of 24. 11⁄12 is equivalent to 22⁄24. 3⁄8 is equivalent to 9⁄24
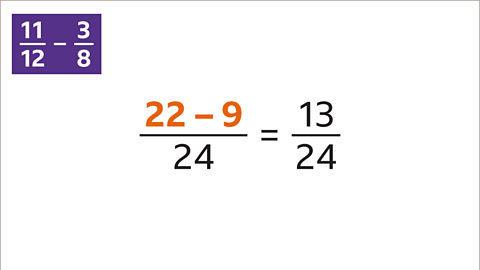
Image caption, Subtract the numerators (22 – 9) of the equivalent fractions, giving an answer of 13⁄24
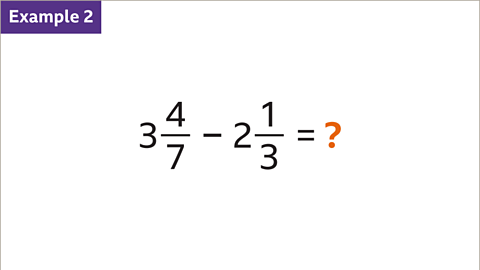
Image caption, Subtract the mixed numbers.
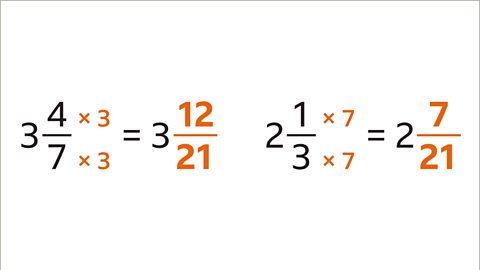
Image caption, The LCM of 7 and 3 is 21. Write equivalent fractions with the same denominator for each mixed number. 4⁄7 is equivalent to 12⁄21. 1⁄3 is equivalent to 7⁄21
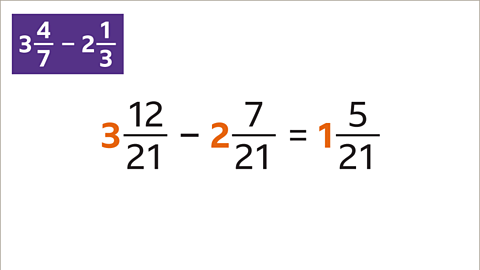
Image caption, Subtract the integers (3 – 2 = 1). Subtract the fractions (12⁄21 – 7⁄21= 5⁄21). 3 4⁄7 – 2 1⁄3 = 1 5⁄21
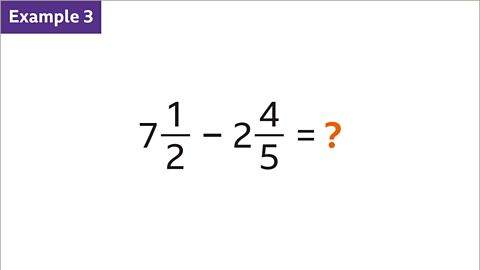
Image caption, Subtract the mixed numbers.
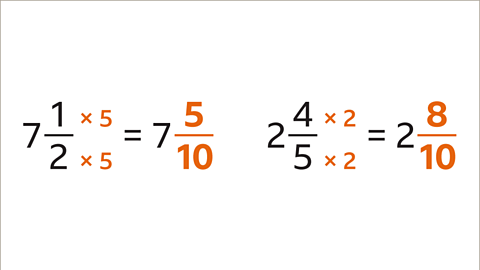
Image caption, The LCM of 2 and 5 is 10. Write equivalent fractions with the same denominator for each mixed number. 1⁄2 is equivalent to 5⁄10. 4⁄5 is equivalent to 8⁄10
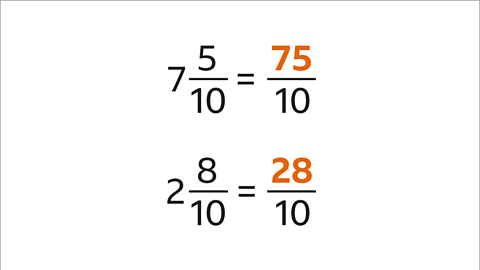
Image caption, The first fraction (5⁄10) is smaller than the second (8⁄10). Change the mixed numbers to improper fractions.
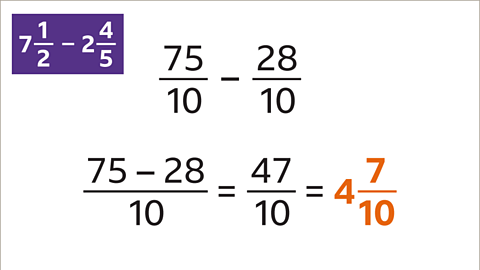
Image caption, Subtract the fractions: 75⁄10 – 28⁄10 = 47⁄10. The answer is 47⁄10. If a mixed number is required, write the answer as 4 7⁄10
1 of 10
Question
Work out \( 4 \frac{2}{5} - 1 \frac{1}{3} \)
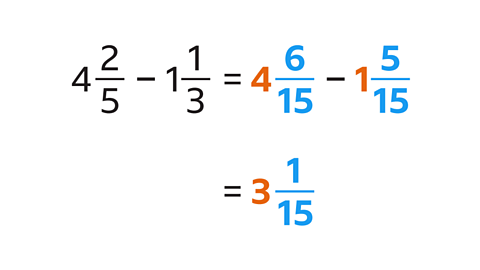
The LCM of 3 and 5 is 15
Write equivalent fractions with the same denominator for each mixed number. \( \frac{2}{5} \) is equivalent to \( \frac{6}{15} \). \( \frac{1}{3} \) is equivalent to \( \frac{5}{15} \)
Subtract the integers. 4 – 1 = 3
Subtract the fractions. \( \frac{6}{15} – \frac{5}{15} = \frac{1}{15} \)
Practise subtracting fractions
Practise what you have learned about subtracting fractions in this quiz. You may need a pen and paper to solve some of these problems.
Real-world maths

Some countries use fractions in measurements when cooking and baking.
These baking recipes measure ingredients in cups, such as \( \frac{1}{4} \) cup of butter or \( \frac{1}{2} \) cup of self-raising flour.

People might subtract fractions when modifying recipes that use cups as a measurement. For example, if a recipe called for \( 2 \frac{1}{2} \) cups of flour, a baker might subtract \( \frac{3}{4} \) from \( 2 \frac{1}{2} \) cups of flour and replace it with \( \frac{3}{4} \) cup of cocoa powder for a chocolate version.
A baker might also subtract \( \frac{1}{4} \) from 1 cup of sugar if they wanted a less sugary version of the recipe.
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Fractions
Find out more by working through a topic
- count8 of 14
- count9 of 14
- count10 of 14
- count11 of 14