Key points
- The productThe result of multiplying one number by another, eg the product of 4 and 5 is 20 since 4 × 5 = 20 of two fractions is calculated by multiplying the numeratorNumber written at the top of a fraction. The numerator is the number of parts used. Eg, for 1⁄3, the numerator is 1 and multiplying the denominatorNumber written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1⁄3, the denominator is 3.
- The word ‘of’ can be replaced by ‘multiplied by’ as it means the same thing. For example,\( \frac{1}{2} \)of\( \frac{1}{3} \)is the same as \( \frac{1}{2} \)multiplied by \( \frac{1}{3} \)
- Sometimes the calculation can be simplified before multiplying.
- mixed numberA number that is written using a whole number and a fraction, eg 3 4⁄5 must be converted to improper fractionA fraction where the numerator is greater than the denominator, eg 9⁄4 before multiplying.
How to multiply fractions
To multiply fractions:
Multiply the numerators.
Multiply the denominators.
Simplify the answer.
The answer may be simplified before calculation using the highest common factor (HCF) The largest factor that will divide into the selected numbers. Eg, 10 is the highest common factor of 30 and 20. Highest common factor is written as HCF.
Examples
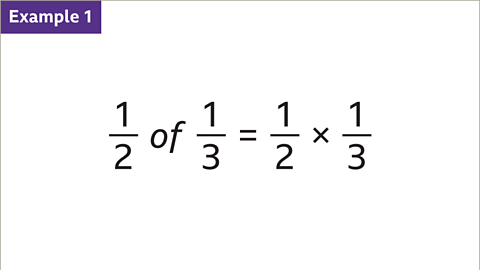
Image caption, 1⁄2 of 1⁄3 is the same as 1⁄2 multiplied by 1⁄3. Work out 1⁄2 of 1⁄3
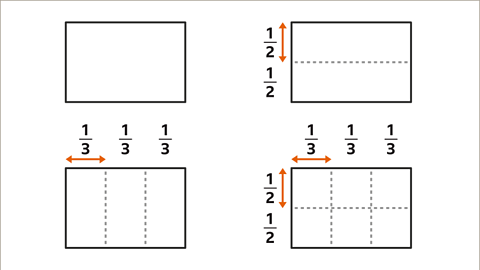
Image caption, Diagrams can be drawn to illustrate this calculation. Draw a rectangle. Split the width into halves. Split the length into thirds. The rectangle is now split into 6 parts (sixths).
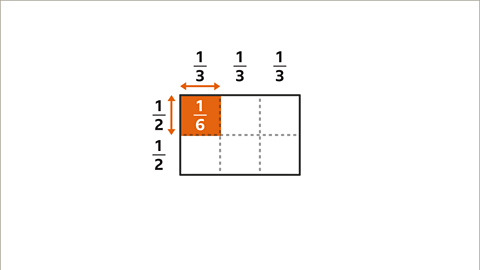
Image caption, 1⁄2 of 1⁄3 is 1⁄6. The product of 1⁄2 and 1⁄3 is 1⁄6 (1⁄2 × 1⁄3 = 1⁄6)
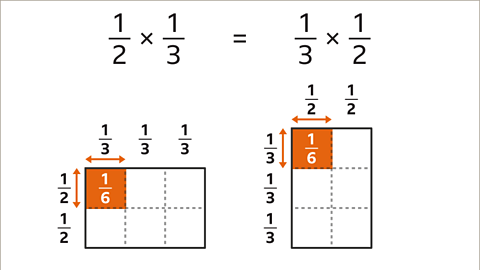
Image caption, Multiplication can be processed in either order. 1⁄2 multiplied by 1⁄3 is the same as a 1⁄3 multiplied by 1⁄2. The rectangle can be used in either orientation. The answer is 1⁄6
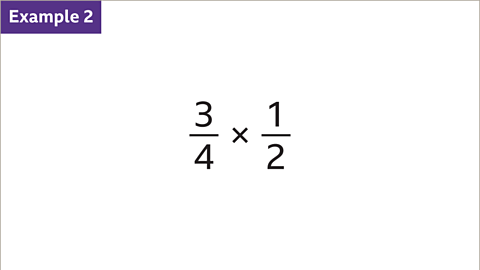
Image caption, Work out 3⁄4 multiplied by 1⁄2
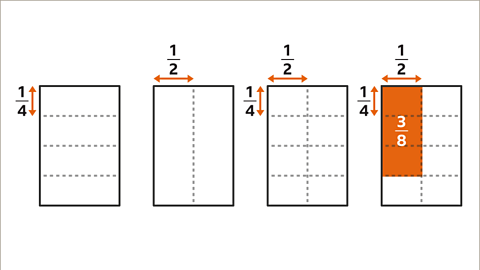
Image caption, To work out 3⁄4 × 1⁄2, draw a rectangle. Split the length into quarters and the width into halves. The rectangle is now split into 8 parts (eighths). 3⁄4 x 1⁄2 = 3⁄8
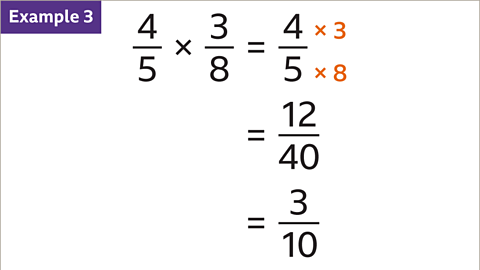
Image caption, To work out 4⁄5 × 3⁄8, multiply the numerators (4 x 3 = 12) and multiply the denominators (5 × 8 = 40). This gives the answer 12⁄40, which can be simplified to 3⁄10. This calculation can also be simplified before multiplying.
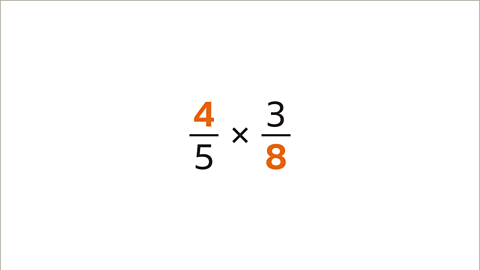
Image caption, The multiplication calculation can be simplified when both a numerator and a denominator have a HCF greater than 1. The HCF of 4 and 8 is 4
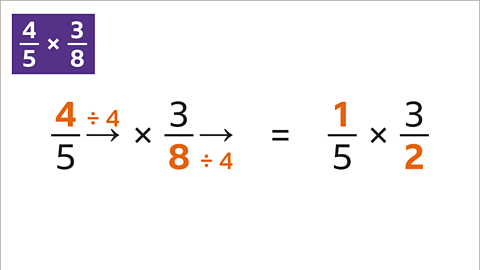
Image caption, Divide 4 and 8 by their HCF (4). The calculation has been simplified to 1⁄5 multiplied by 3⁄2
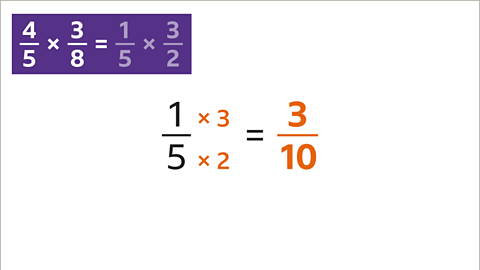
Image caption, 1⁄5 × 3⁄2 gives the same answer as 4⁄5 × 3⁄8. The simplifying has been done first to make the calculation easier. 4⁄5 × 3⁄8 = 3⁄10
1 of 10
Question
Find the product of\( \frac{2}{9} \)and\( \frac{4}{5} \)
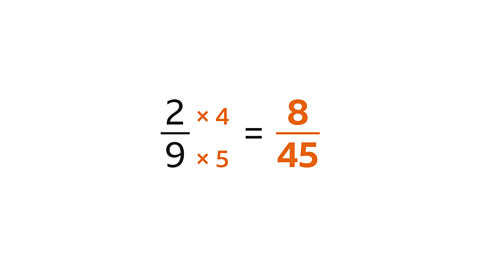
To find the product of the fractions, multiply the numerators (2 and 4) and multiply the denominators (9 and 5). The product is\( \frac{8}{45} \)
How to multiply mixed numbers
To multiply mixed numbers:
Rewrite the mixed numberA number that is written using a whole number and a fraction, eg 3 4⁄5 as improper fractionA fraction where the numerator is greater than the denominator, eg 9⁄4. This is done by multiplying the integer by the denominator and adding the numerator.
If possible, simplify before calculating using the highest common factor (HCF) The largest factor that will divide into the selected numbers. Eg, 10 is the highest common factor of 30 and 20. Highest common factor is written as HCF.
Multiply the numerators.
Multiply the denominators.
Simplify the answer if possible.
Examples
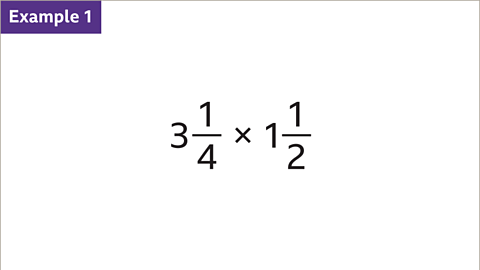
Image caption, Multiply 3 1⁄4 by 1 1⁄2
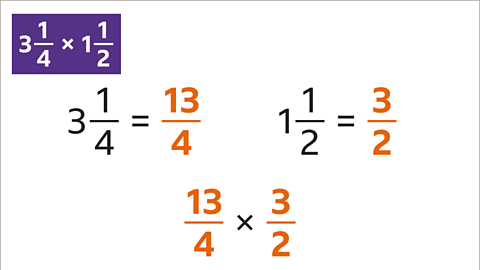
Image caption, Convert each mixed number into an improper fraction. The calculation becomes 13⁄4 × 3⁄2
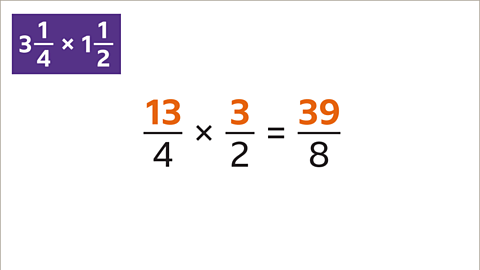
Image caption, Multiply the numerators and multiply the denominators.
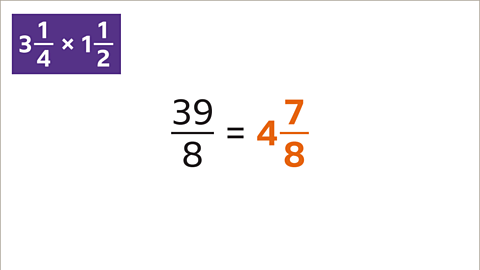
Image caption, The improper fraction can be written as a mixed number. 39⁄8 is 4 7⁄8
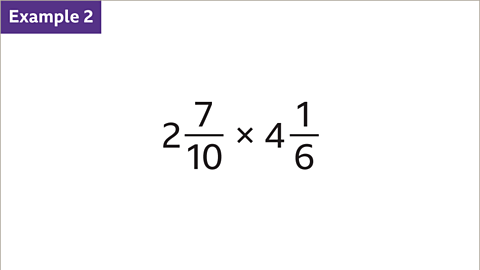
Image caption, Multiply 2 7⁄10 by 4 1⁄6
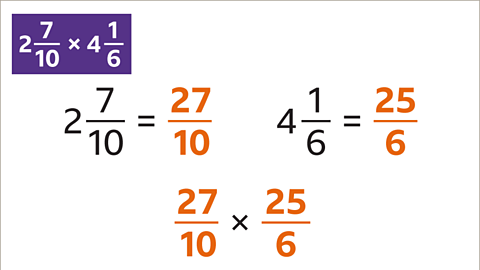
Image caption, Convert each mixed number into an improper fraction. The calculation becomes 27⁄10 × 25⁄6. This can be simplified.
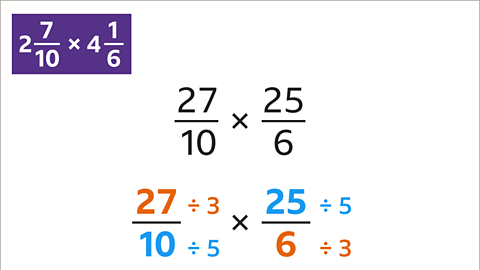
Image caption, The HCF of 27 and 6 is 3. The HCF of 10 and 25 is 5. Divide by these factors.
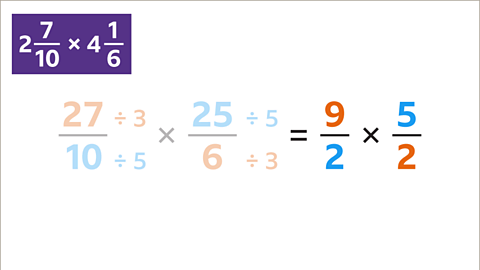
Image caption, The calculation has been simplified to 9⁄2 × 5⁄2
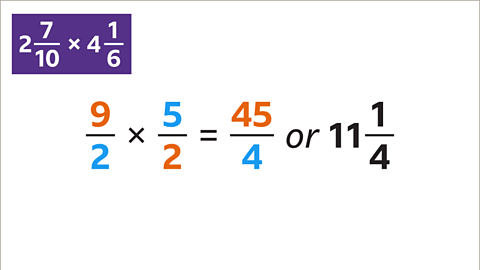
Image caption, 9 x 5 = 45. 2 x 2 = 4. 45⁄4 is 11 1⁄4 as a mixed number.
1 of 9
Question
Find the product of \( 3\frac{1}{4} \) and \( 2\frac{2}{3} \)
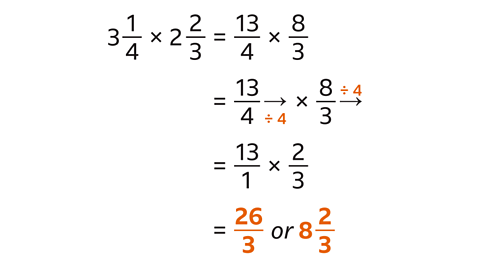
Convert the mixed numbers into improper fractions.
Simplify the calculation by dividing a numerator and a denominator by their highest common factor (4)
Multiply the numerators (13 and 2) and multiply the denominators (1 and 3)
The product is \( \frac{26}{3} \) which is \( 8 \frac{2}{3} \)as a mixed number.
Practise multiplying fractions
Try this quiz to practise multiplying fractions. You may need a pen and paper to solve some of these problems.
Quiz
Real-world maths

In genetics (the study of how genes and characteristics are passed down), multiplying by fractions can help track and predict the likelihood of features being passed onto a child, such as freckles or hair colour.
Half of a child’s genes come from one parent and half from another. When both parents carry the gene for a particular feature, they each have a chance of passing this on to the child.
By multiplying fractions, the chance of the child inheriting that feature can be worked out. For example, if both parents have\( \frac{1}{2} \)a chance of passing a feature on, the likelihood of inheriting is\( \frac{1}{4}\).

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Fractions
Find out more by working through a topic
- count9 of 14
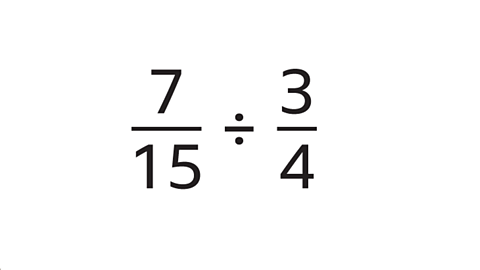
- count10 of 14
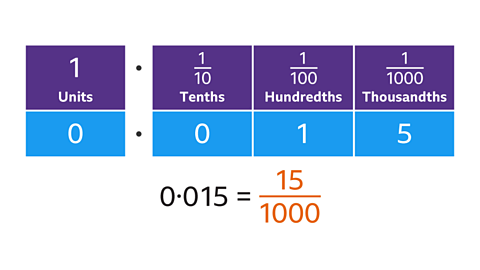
- count11 of 14
- count12 of 14
