Key points
- To divide a fraction by a fraction use the reciprocalThe reciprocal of a number is 1 divided by the number. For example the reciprocal of 2 is 1⁄2, the reciprocal of 3⁄4 is 4⁄3. A number multiplied by its reciprocal is 1 method. This means to turn the second fraction upside down and multiply.
- Sometimes calculations can be simpler using fractions rather than their decimal equivalents.
- Understanding improper fractions and mixed numbers conversions may help when dividing fractions. Knowing how to multiply fractions may also be useful.
How to divide by a fraction
- To divide with fractions, it can be useful to think about how many times a fraction will fit into a number or another fraction.
- For example, when dividing 5 by ½, you are asking how many halves there are in 5
- This may help you to understand the reciprocal method.
Example: calculate 5 ÷ 1⁄2

Image caption, How many halves are there in 5?
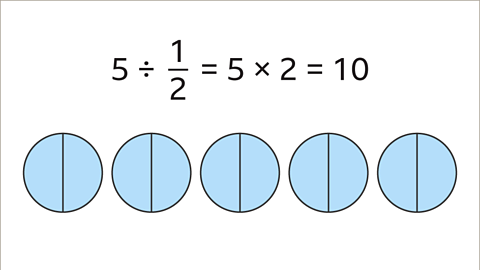
Image caption, Dividing by ½ is the same as multiplying by 2. There are 10 halves in 5
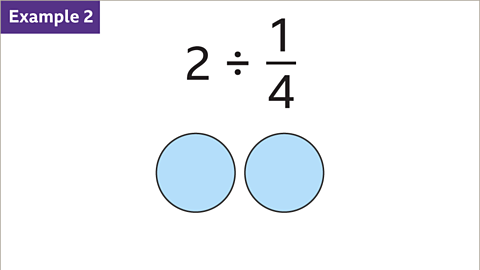
Image caption, How many quarters are there in 2?
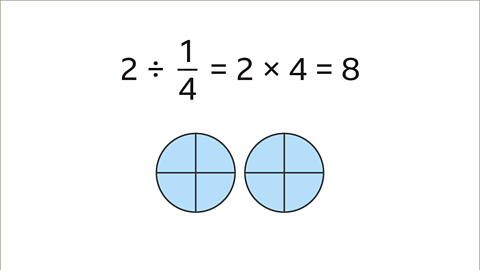
Image caption, Dividing by a quarter is the same as multiplying by 4. There are 8 quarters in 2
1 of 4
Reciprocal method
- To divide a fraction by a fraction use the reciprocalThe reciprocal of a number is 1 divided by the number. For example the reciprocal of 2 is 1⁄2, the reciprocal of 3⁄4 is 4⁄3. A number multiplied by its reciprocal is 1 method.This means to turn the second fraction upside down and multiply.
- simplify (a fraction)To reduce a fraction to its simplest form, also known as its lowest terms. the answer where necessary.
Example: calculate 10⁄3 ÷ 2⁄3
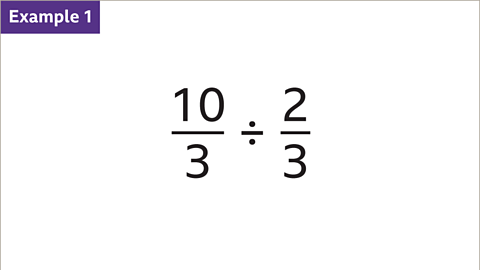
Image caption, Calculate 10⁄3 ÷ 2⁄3
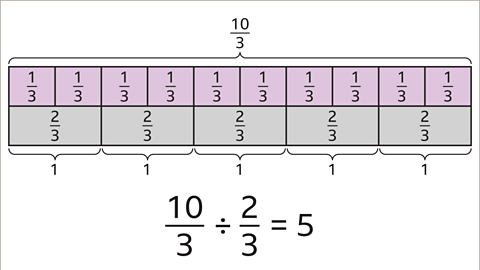
Image caption, The diagram shows that 2⁄3 fits into 10⁄3 five times.
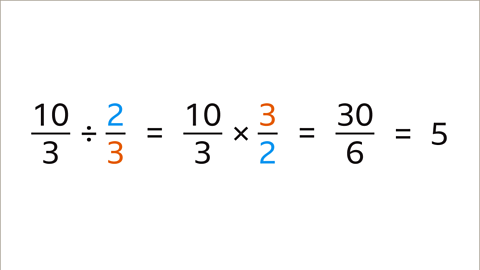
Image caption, To divide these fractions use the reciprocal method. Turn the second fraction 2⁄3 upside down. Multiply 10⁄3 by 3⁄2. This is 30⁄6 which simplifies to 5
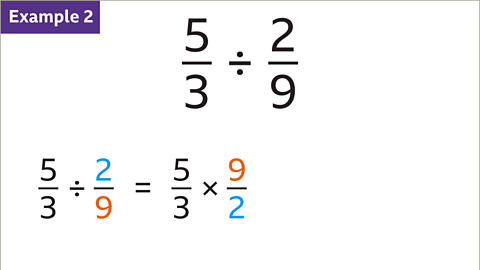
Image caption, To divide these fractions use the reciprocal method. Turn the second fraction 2⁄9 upside down. Multiply 5⁄3 by 9⁄2
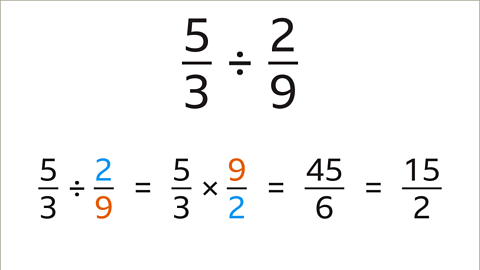
Image caption, 5⁄3 × 9⁄2 = 45⁄6. This simplifies to 15⁄2
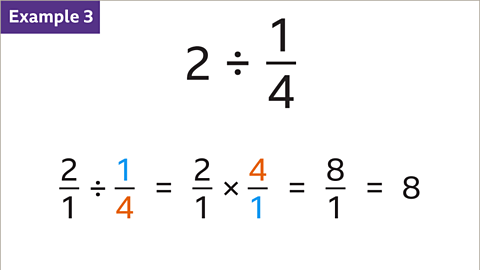
Image caption, Remember that 2 is the same as 2⁄1. 2⁄1 × 4⁄1 = 8⁄1 = 8. Write the answer as simply as possible.
1 of 6
Work out 7⁄15 ÷ 3⁄4
Use the reciprocal method to divide by a fraction.Turn the second fraction upside down and multiply.
For any fraction, \( \frac{a}{b} \)
\( ? ÷ \frac{a}{b} \) is the same as \( ? × \frac{b}{a} \)
Question
Calculate \( \frac{7}{15} ÷ \frac{3}{4} \)
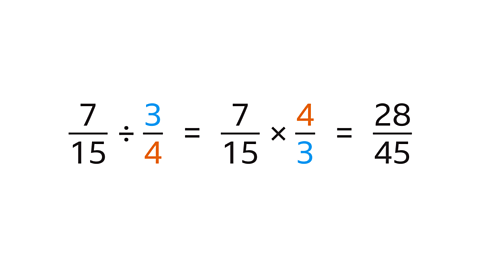
The reciprocal of \( \frac{3}{4} \) is \( \frac{4}{3} \)
This is because \( \frac{3}{4} × \frac{4}{3} = \frac{12}{12} = 1 \)
The fraction in its simplest form is \( \frac{7}{15} ÷ \frac{3}{4} = \frac{7}{15} × \frac{4}{3} = \frac{28}{45} \)
Practise dividing fractions
Work out 2 1⁄4 ÷ 3⁄5
Hint: Understanding how to convert between mixed numbers and improper fractions can be useful when dividing fractions. It might be useful to have a pen and paper to help with your workings.
Dividing fractions quiz
Try practising dividing fractions with this quiz. You might need a pen and paper to solve these questions.
Real-world maths

Calculating average speed
Competitors in the Eco-marathon, a fuel economy competition, must have an average speed of at least 15 miles per hour (mph) to qualify.

Question
At one Eco-marathon race, the distance driven was 9 \( \frac{1}{2} \) miles, a car completed the race in 32 minutes.Was the average speed enough to qualify?
Distance 9 \( \frac{1}{2} \) miles = \( \frac{19}{2} \) miles
Time 32 minutes = \( \frac{32}{60} \) hours = \( \frac{8}{15} \) hours
Average speed = distance ÷ time
\( \frac{19}{2} ÷ \frac{18}{15} = \frac{19}{2} × \frac{15}{8} = \frac{285}{16} = 17 \frac{13}{16} \) mph
\( 17 \frac{13}{16} \) is greater than 15, this competitor did qualify.
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Fractions
Find out more by working through a topic
- count10 of 14
- count11 of 14
- count12 of 14

- count13 of 14