Key points
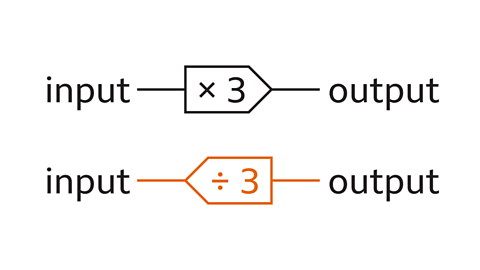
A functionOne or more operations that are applied to an input to give an output. relates an input to an output. One or more operationsA rule for combining numbers. For example, addition, subtraction, multiplication and division are all operations. are applied to an input to give an output. There is one output for a given input.
A function may be represented:
- using function machineUsed to visually present a single-step function. A multi-step function can be presented using multiple function machines.
- as an expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms. (or an equation)
- as a graph
An input value becomes an output value when the operations of a function machine are worked through from left to right.
An input value can be found from the output when the inverse operationThe opposite of a mathematical process. Eg, the inverse of × 5 is ÷ 5. The inverse operation undoes the original process. are worked through from right to left.
Understanding the correct order of operations (using BIDMAS) is useful when using function machines to write expressions.

Using function machines
A single function machine represents a one-step function. To use a single function machine (input → output):
Start with the input.
Work through the function machine operation from left to right. The output is the result of the calculation.
A multi-step function can be presented using multiple function machines. To use a multi-step function machine (input → output):
Start with the input.
Work through each function machine operation for each step from left to right. The output of each step becomes the input for the next step to the right. The final output is the result of the whole calculation.
An input value can be found from the output value by working through the inverse operations of the function machine from right to left.
Examples
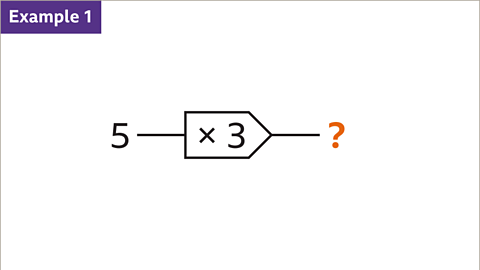
Image caption, A single function machine is used for one operation. An input is processed to give an output. The input for this function machine is 5. The output is unknown.
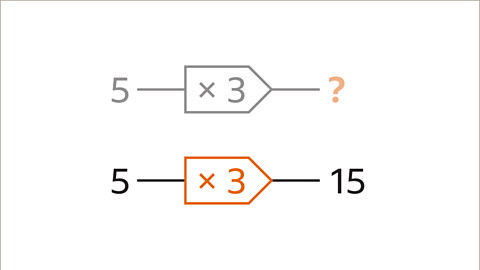
Image caption, To find the output, start with the input (5). Process the function machine operation. 5 is multiplied by 3. The output is the result of the calculation. 5 × 3 = 15. The output is 15
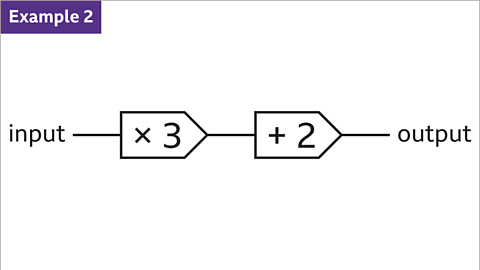
Image caption, A multi-step function machine may be used for more than one operation. To find the output, the operations are worked through from left to right.
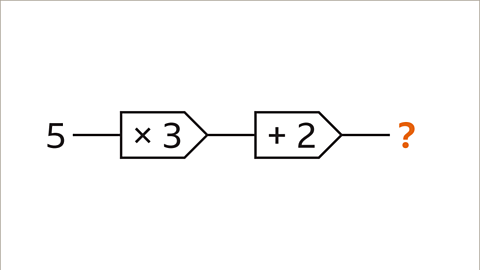
Image caption, The input is 5 and the output is unknown. The 2-step function machine shows two operations. The first step is to multiply by 3. The second step is to add 2
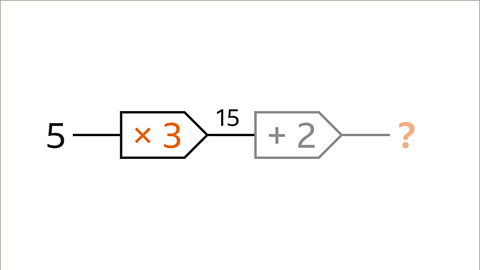
Image caption, To find the output, start with the input (5). Work through the first step. 5 × 3 = 15. The output (15) becomes the input for the next step to the right.
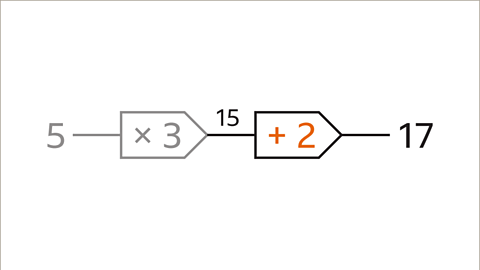
Image caption, The output of the previous step (15) is the input for the second step. Work through the second calculation (15 + 2). The output is the result of all the working out. 3 × 5 = 15 and 15 + 2 = 17. The output is 17
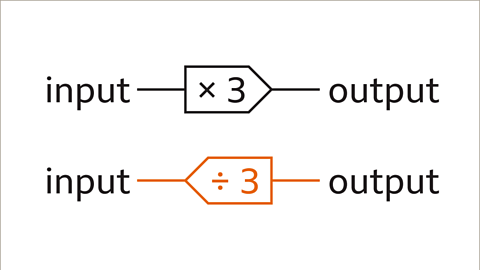
Image caption, Function machines may be used in reverse order. Work through the inverse operations from a given output to find the original input. The inverse of multiplication is division.
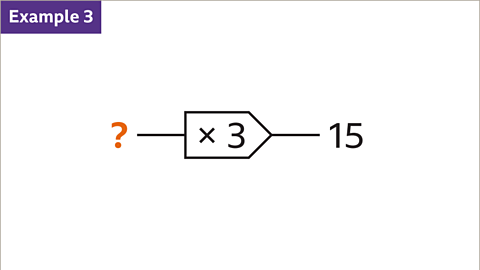
Image caption, The output is 15. The input is unknown.
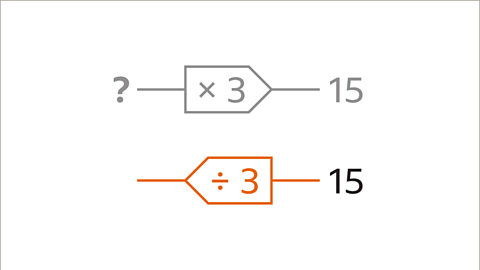
Image caption, Write the inverse function machine so that the direction goes from right to left. Write the inverse operation in the function machine. The inverse of multiply by 3 is divide by 3
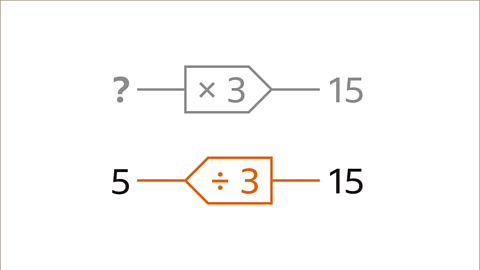
Image caption, Start with the output (15). Work through the inverse operation (15 ÷ 3). The input is the result of the inverse calculation. 15 ÷ 3 = 5. The input is 5
1 of 10
Question
Work out the input for the 3-step function machine.
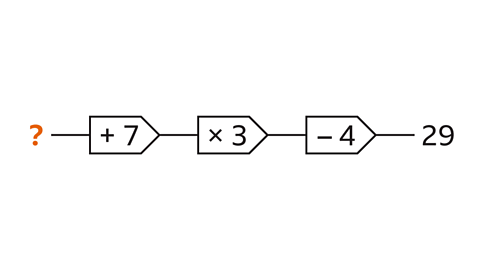
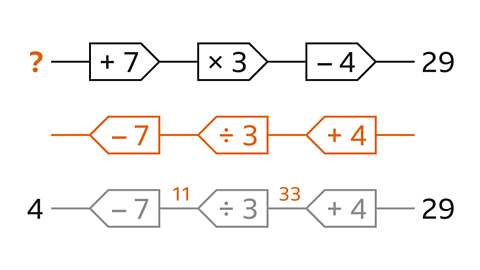
- Write the inverse 3-step function machine so that the direction works from right to left. Write the inverse operation for each step:
- The inverse of subtract 4 is add 4
- The inverse of multiply by 3 is divide by 3
- The inverse of add 7 is subtract 7
- Start with the output (29). Work through each inverse operation from right to left:
- 29 + 4 = 33. The output is 33 for the next step to the left.
- 33 ÷ 3 =11 . The output is 11 for the next step to the left.
- 11 – 7 = 4. The input is 4
Using function machines to write expressions
When the input to a function machine is a variableAn unknown value, usually represented by a letter like 𝒙 or 𝒚, the output is anexpressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms..
One function gives a single term output. The expression will have more terms when there are more steps in the function machine.
To write an expression from a function machine:
Start with the variable.
Work through the operation for each step from left to right.
Write the expression using the correct algebraic notationA series or system of written symbols used to represent numbers, amounts or elements in mathematics. for each process.
Use brackets when an operation applies to more than one term.
Understanding notation used in algebra will help when writing expressions.
Examples
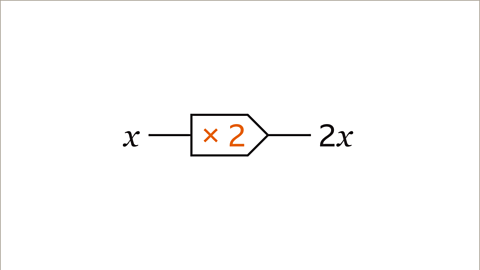
Image caption, For a variable input, the output is an expression.
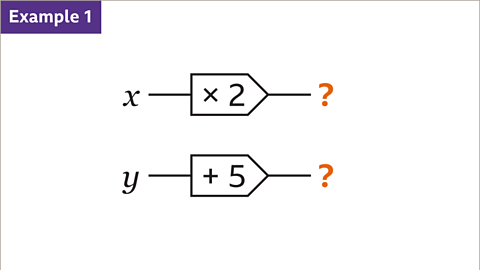
Image caption, For each function machine, the output is an algebraic expression.
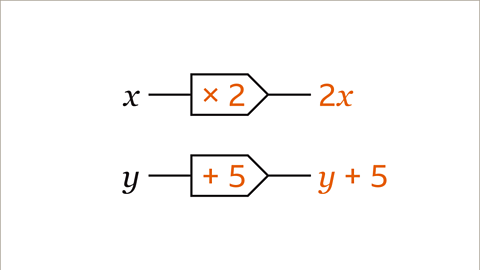
Image caption, Start with the variable (𝒙 and 𝒚). Work through the operation for each function machine from left to right using the correct algebraic notation for each process. 𝒙 multiplied by 2 is 2𝒙. 𝒚 plus 5 is 𝒚 + 5
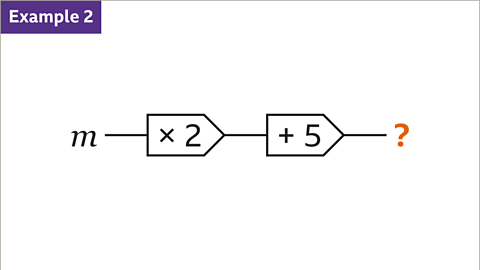
Image caption, Write the expression for this 2-step function machine.
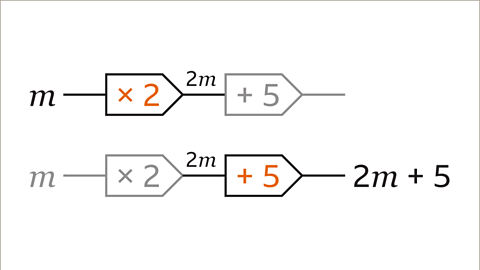
Image caption, Start with the variable (𝒎). Work through the operation for each step from left to right. 𝒎 multiplied by 2 is 2𝒎. Adding 5 gives the expression 2𝒎 + 5
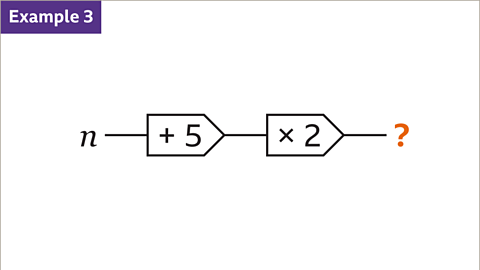
Image caption, Write the expression for this 2-step function machine.
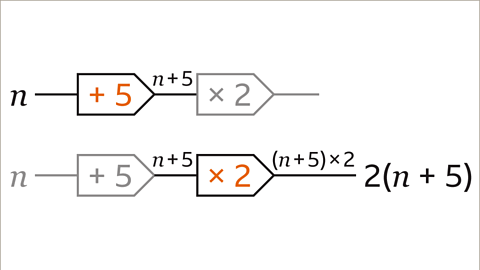
Image caption, Start with the variable (𝒏). Work through the operation for each step in the function machine from left to right. 𝒏 plus 5 is 𝒏 + 5. The whole of 𝒏 + 5 is multiplied by 2 and brackets are used to show this. Write the expression with the correct notation. The expression is 2(𝒏 + 5).
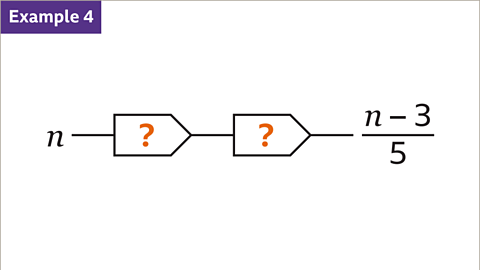
Image caption, For an input of 𝒏, a 2-step function machine gives the output 𝒏 − 3, all over 5. Write the correct operations to complete the steps for the function machine.
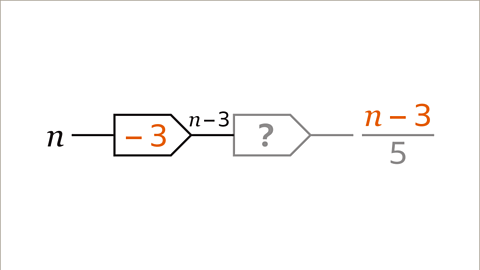
Image caption, The first operation that has been used on 𝒏 is subtract 3. This is 𝒏 − 3. The first step is − 3
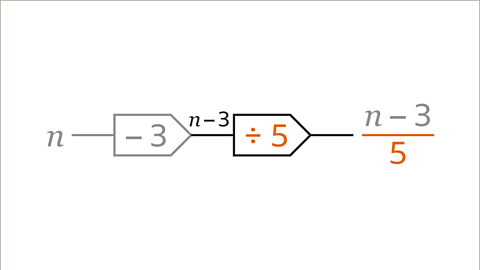
Image caption, The next part of the expression is a division. 5 is the denominator of a fraction, so the operation is divide by 5. The second step for the function machine is ÷ 5
1 of 10
Question
Write the expression for this 3-step function machine.
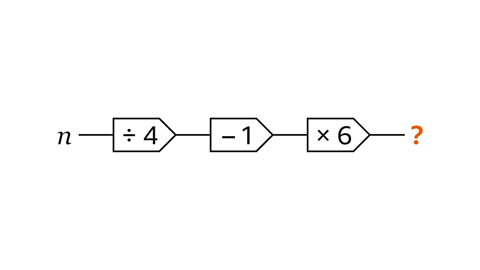
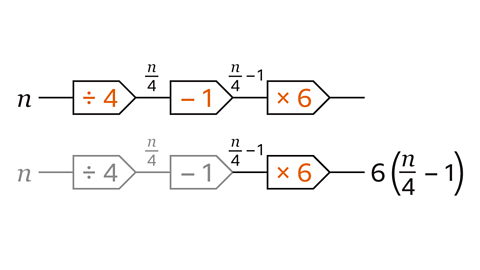
Start with the variable (𝒏).
Work through the operation for each step in the function machine from left to right:
- 𝒏 divided by 4 is \( \frac{𝒏}{4} \)
- 1 is subtracted giving \( \frac{𝒏}{4} \) − 1
- The whole of \( \frac{𝒏}{4} \) − 1 is multiplied by 6 and brackets are used to show this.
The expression for this 3-step function machine is 6 (\( \frac{𝒏}{4} \) − 1)
Practise using function machines
Practise using function machines with this quiz. You may need a pen and paper to help you work out your answers.
Quiz
Real-life maths
Functions are used in real life as a single-, or multi-step, set of processes. For example, turning the dial on a shower to a higher setting increases the volume or temperature of the water. Turning the dial is the input and the increased volume or temperature of the water are the output.
Functions are also used to process information. A 'sat nav' (satellite navigation system) identifies a sequence of directions to help you get to your destination. The order in which these directions are followed is important. The directions and steps of the journey are the input and the destination is the output.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Expressions and formulae
Find out more by working through a topic
- count3 of 8
- count5 of 8