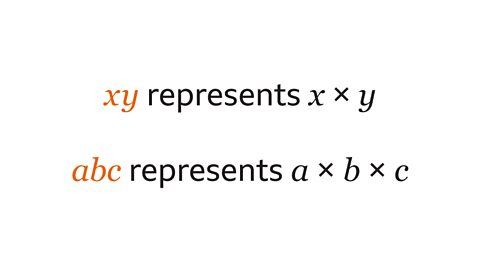Key points
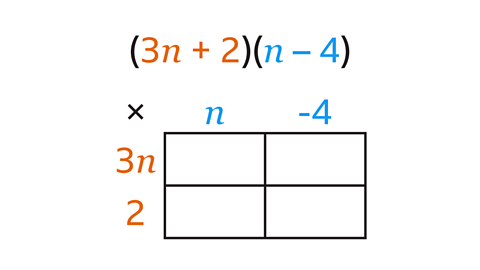
When expanding brackets it’s important to have a good understanding of multiplying terms, multiplying by positive and negative numbers and index notation.
To expand a single bracket, each termAn element within an algebraic sentence. Elements (terms) are separated by + or - signs. inside the bracket is multiplied by the expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms. outside the bracket.
It may be possible to simplifyRewrite an expression so that it has fewer terms. An expression may be simplified using addition, subtraction, multiplication or division. the expression after expanding the bracket. This is done by collecting the like termsTerms whose variables (such as 𝒙 or 𝒚) with any exponents (a symbol written above and to the right of a mathematical expression) are the same. For example, 7𝒙 and 2𝒙 are like terms because they are both amounts of ‘𝒙’..
One bracket may be multiplied by another bracket. This is sometimes called expanding double brackets.
To expand double brackets, every term in the first bracket must be multiplied by every term in the second bracket. It may be possible to simplify the resulting expression.
The expression that results from expanding a single or a double bracket and the original expression are identity ≡An equation that is true no matter what values are chosen. The identity symbol ≡ links expressions that are identities.. They are equivalent expressionA numerical or algebraic expression which is the same as the original expression but is in a different form. Equivalent expressions are identically equal. The identity symbol, ≡, can link equivalent expressions. expressions.
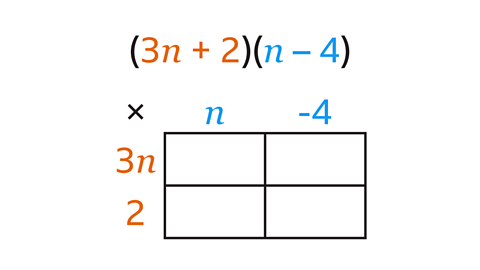
Expanding a single bracket
To expand a single bracket multiply each term inside the bracket by the term outside the bracket.
If the term and the bracket are joined by an addition or subtraction symbol, the term is not multiplied by the expression in the bracket.
An addition sign before the bracket means each term is multiplied by 1. A subtraction sign in front of the bracket means each term is multiplied by –1.
When an expression includes multiple single brackets:
Expand each bracket in the expression by multiplying each term in the bracket by the term in front of the bracket.
Simplify the expression by collecting the like terms.
The starting expression, with a bracket (or brackets), is equivalent to the resulting expression. They are identities.
Examples
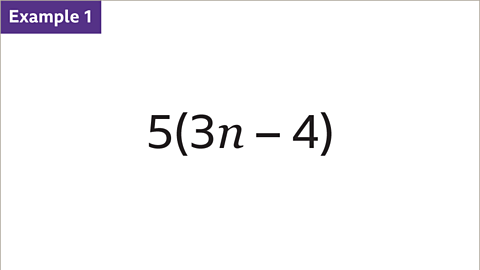
Image caption, Expand the expression 5(3𝒏 – 4).
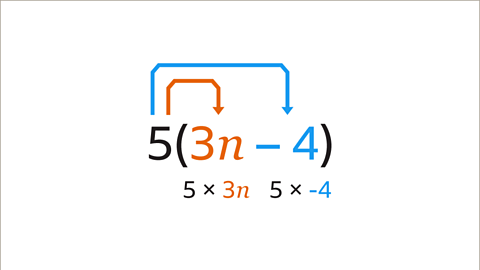
Image caption, The term in front of the bracket (5) is multiplied by each term inside the bracket. The calculations are 5 × 3𝒏 and 5 × –4
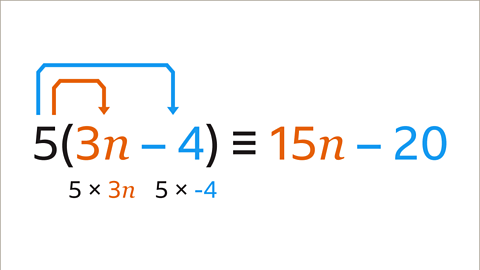
Image caption, 5 × 3𝒏 = 15𝒏. 5 × –4 = –20. 5(3𝒏 – 4) is equivalent to 15𝒏 –20. They are identities.
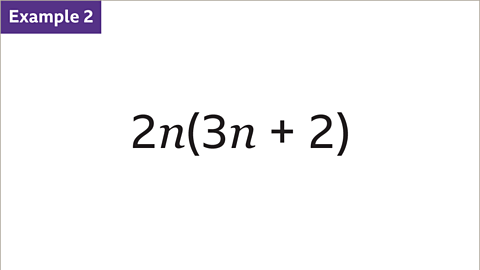
Image caption, Expand 2𝒏(3𝒏 + 2).
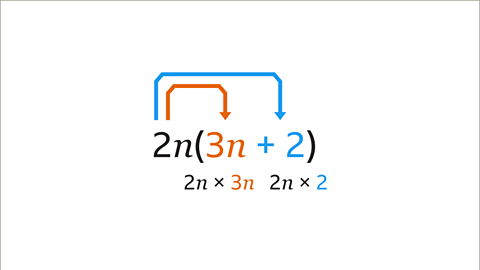
Image caption, The term in front of the bracket (2𝒏) is multiplied by each term inside the bracket. The calculations are 2𝒏 × 3𝒏 and 2𝒏 × 2
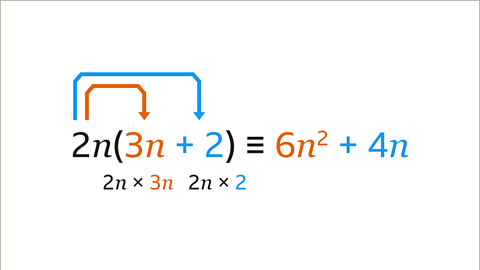
Image caption, 2𝒏 × 3𝒏 = 6𝒏². 2𝒏 × 2 = 4𝒏. 2𝒏(3𝒏 + 2) is equivalent to 6𝒏² + 4𝒏. They are identities.
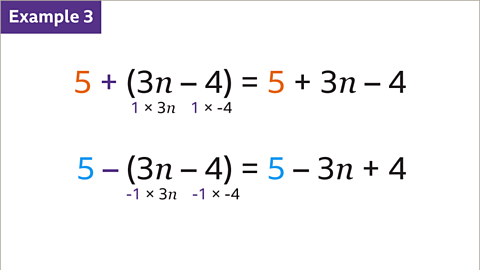
Image caption, If there is an addition or subtraction symbol between a term and a bracket, the term is separated from the bracket. The bracket is not multiplied by that term. The expression can be written without the bracket. An addition sign before the bracket means each term is multiplied by 1. The terms stay the same, + 3𝒏 – 4. As this includes a subtraction the terms change signs. 3𝒏 becomes – 3𝒏 and – 4 becomes + 4. The expressions must now be simplified.
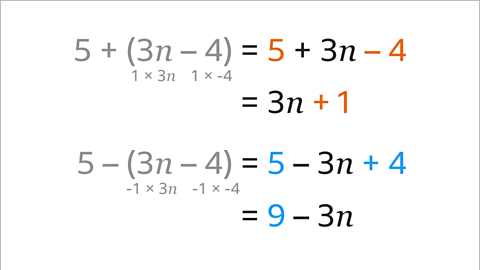
Image caption, The expressions are simplified by collecting the like terms. The sign in front of each term stays with that term. For the first expression, 5 – 4 = 1 and 5 + (3𝒏 – 4) becomes 3𝒏 + 1. For the second expression, 5 + 4 = 9 and 5 – (3𝒏 – 4) becomes 9 – 3𝒏. This may also be written as – 3𝒏 + 9
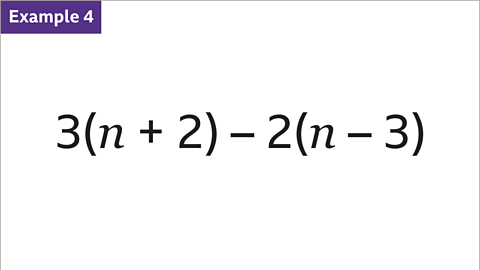
Image caption, Expand and simplify 3(𝒏 + 2) – 2(𝒏 – 3).
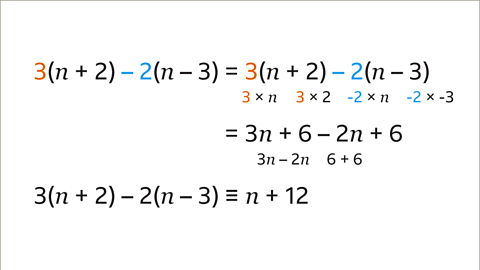
Image caption, Expand each bracket in the expression. Multiply each term in the bracket by the term attached to the front of the bracket. For the first bracket, 3 is multiplied by 𝒏 and 2. For the second bracket, –2 is multiplied by 𝒏 and –3. The expression is now 3𝒏 + 6 – 2𝒏 + 6. This expression can be simplified by collecting the like terms. 3𝒏 – 2𝒏 = 𝒏 and 6 + 6 = 12. This expression can be simplified. 3(𝒏 + 2) – 2(𝒏 – 3) is equivalent to 𝒏 + 12. They are identities.
1 of 10
Questions
Question 1: Expand the bracket.
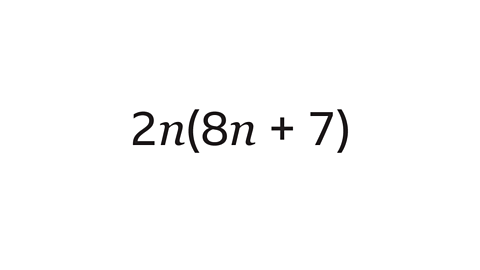
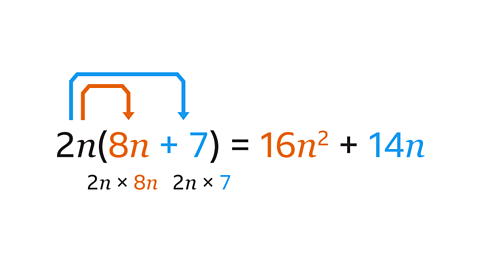
The term in front of the bracket (2\(n\)) is multiplied by each term inside the bracket.
The calculations are 2\(n\) × 8\(n\) = 16\(n\)² and 2\(n\) × 7 = 14\(n\)
2\(n\)(8\(n\) + 7) is equivalent to 16\(n\)² + 14\(n\), they are identities.
Question 2: Expand and simplify the expression.
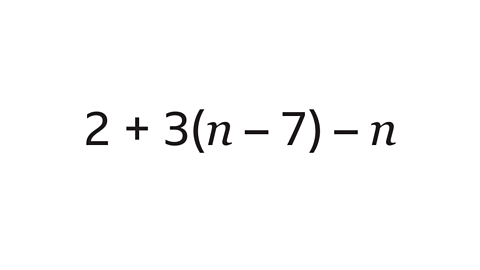
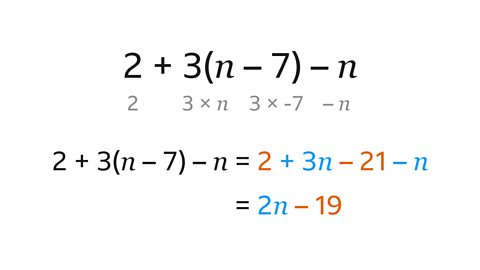
The expression has one bracket that must be expanded and two other terms: 2 and -\(n\)
The bracket 3(\(n\) - 7) expands to give 3\(n\) – 21
The expression becomes 2 + 3\(n\) – 21 – \(n\). This can be simplified by collecting the like terms.
The like terms are the constants 2 and –21 and the variables 3\(n\) and – \(n\)
The expression simplifies to 2\(n\) – 19
Expanding double brackets
- To expand double brackets using a grid:
Multiply each term in the first bracket by each term in the second bracket. When there are two terms in each bracket, use a 2 x 2 grid. The dimensions of the grid match the number of terms in each bracket.
Write the terms for the first bracket on the left side of the grid and the terms in the second bracket across the top of the grid.
Fill in the grid by multiplying each term in the first bracket by each term in the second bracket.
Write the expression with all four terms.
Simplify the expression by collecting the like terms.
- To expand double brackets without using a grid:
Multiply each term in the first bracket by each term in the second bracket.
Rewrite the expression so that the first bracket is split to show each term is multiplied by the second bracket. The expression now has two single brackets to expand.
Expand each single bracket.
Simplify the expression by collecting the like terms. The starting expression (with brackets) is equivalent to the resulting expression. They are identities.
Examples
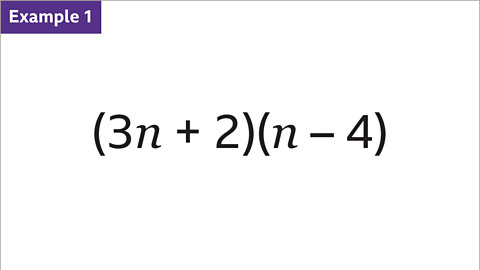
Image caption, Expand (3𝒏 + 2)(𝒏 – 4).
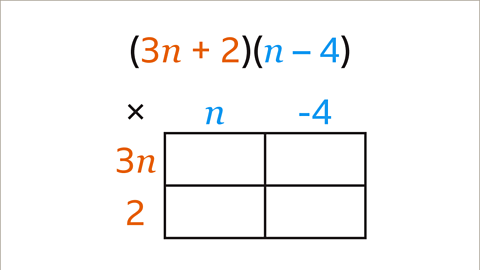
Image caption, Each term in the first bracket is multiplied by each term in the second bracket. There are two terms in each bracket so a 2 x 2 grid is used. Write the terms in the first bracket to the left of the grid and the terms in the second bracket across the top of the grid.
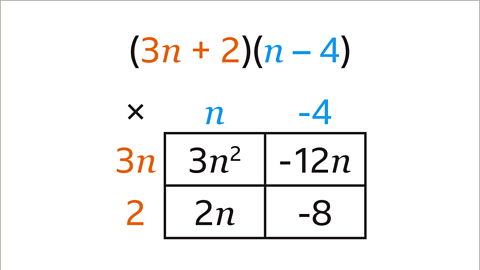
Image caption, Complete the grid by multiplying each term in the first bracket by each term in the second bracket. 3𝒏 × 𝒏 = 3𝒏². 3𝒏 × –4 = –12𝒏. 2 × 𝒏 = 2𝒏. 2 × –4 = –8
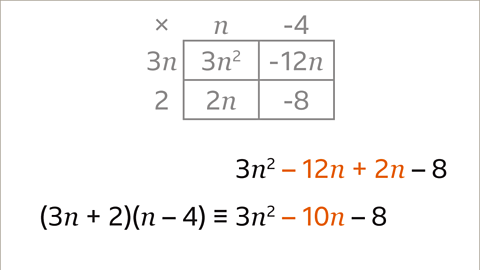
Image caption, Write the expression with all four terms. Simplify the expression by collecting the like terms. (3𝒏 + 2)(𝒏 – 4) is equivalent to 3𝒏² – 10𝒏 – 8. They are identities.
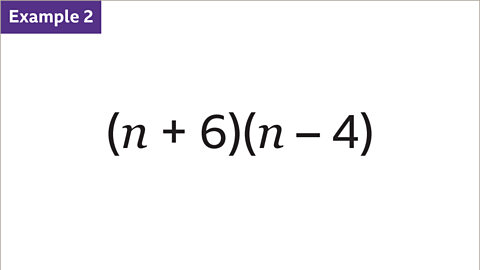
Image caption, Expand and simplify (𝒏 + 6)(𝒏 – 4) without a grid.
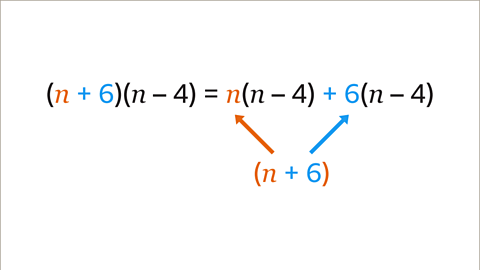
Image caption, Rewrite the expression. The first term in the first bracket (𝒏) is multiplied by the second bracket, this is 𝒏(𝒏 – 4). The second term in the first bracket (6), is multiplied by the second bracket, this is + 6(𝒏 – 4). The expression now has two single brackets to expand.
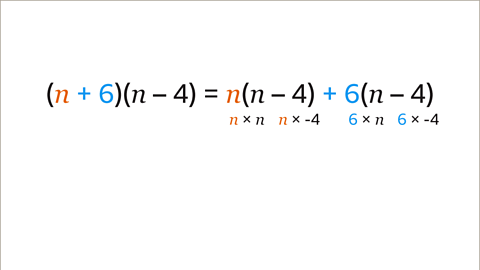
Image caption, Expand each single bracket. Each term in (𝒏 – 4) is multiplied by 𝒏. Each term in (𝒏 – 4) is multiplied by 6
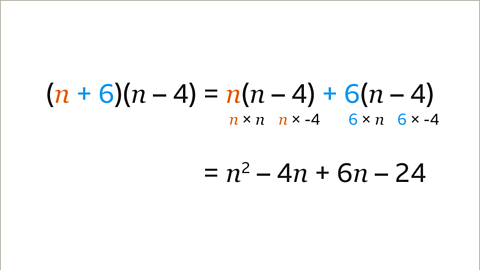
Image caption, (𝒏 + 6)( 𝒏 – 4) expands to give the expression 𝒏² – 4𝒏 + 6𝒏 – 24. This expression can be simplified.
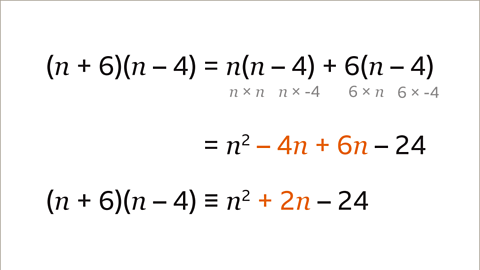
Image caption, 𝒏² – 4𝒏 + 6𝒏 – 24 can be simplified by collecting the like terms ( – 4𝒏 and 6𝒏). (𝒏 +6)(𝒏 – 4) is equivalent to 𝒏² + 2𝒏 – 24. They are identities.
1 of 9
Questions
Question 1: Expand and simplify the expression.
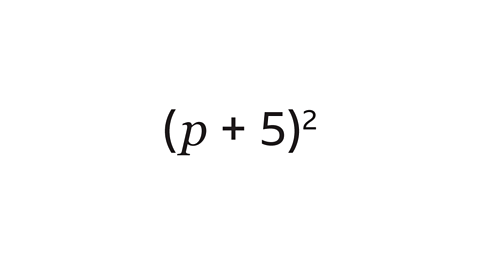
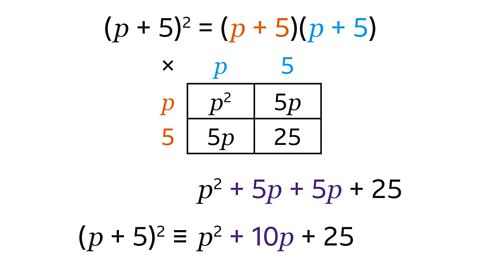
(\(p\) + 5)² means (\(p\) + 5)(\(p\) + 5). Each term in the first bracket is multiplied by each term in the second bracket.
There are two terms in each bracket so a 2 x 2 grid is used. To expand and simplify the expression:
Write the terms for the first bracket to the left of the grid, and the terms in the second bracket across the top.
Fill in the grid by multiplying each term in the first bracket by each term in the second bracket:
\(p\) × \(p\) = \(p\)². \(p\) × 5 = 5\(p\). 5 × \(p\) = 5\(p\). 5 × 5 = 25Write the expression with all four terms.
Simplify the expression by collecting the like terms.
(\(p\) + 5)² is equivalent to \(p\)² + 10\(p\) + 25. They are identities.
Question 2: Expand and simplify the expression.
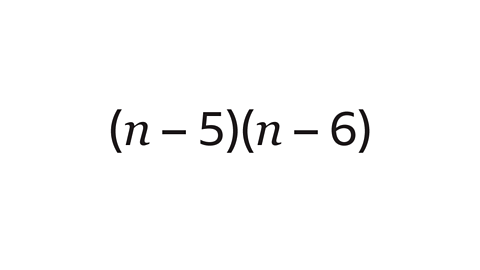
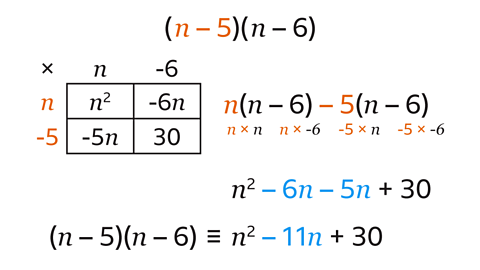
Each term in the first bracket is multiplied by each term in the second bracket. To expand and simplify the expression:
Use a 2 x 2 grid or work without a grid.
Rewrite the expression so that the first bracket is split to show each term is multiplied by the second bracket. The expression now has two single brackets to expand.
\(n\) is multiplied by (\(n\) – 6) and –5 is multiplied by (\(n\) – 6).Expand each single bracket:
\(n\) (\(n\) – 6) = \(n\)² – 6\(n\). –5(\(n\) – 6) = – 5\(n\) + 30Simplify the expression by collecting the like terms:
\(n\)² – 6\(n\) – 5\(n\) + 30 ≡ \(n\)² – 11\(n\) + 30
Practise multiplying brackets
Quiz
Practise multiplying brackets with this quiz. You may need a pen and paper to help you work out your answers.
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Expressions and formulae
Find out more by working through a topic
- count7 of 8
- count8 of 8
- count1 of 8