How to multiply and divide positive and negative numbers – KS3 Maths

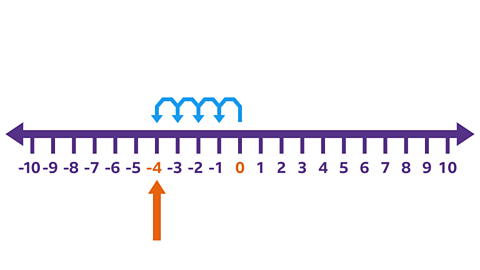
Key points

Multiplication is . This means that the order in which you multiply a pair of numbers does not make a difference, eg 3 x 5 = 5 x 3
The is the answer when two or more numbers are multiplied together.
Calculations can be written with brackets around negative numbers because this can make a calculation easier to read, eg -3 × -1 is the same calculation as (-3) × (-1)
Learning about positive and negative numbers will help when multiplying and dividing negative numbers.

When multiplying negative numbers it is often useful to complete the calculation using positive numbers initially.Then remember that:

multiplying two numbers together with the same sign gives a positive answer
multiplying two numbers together with different signs gives a negative answer

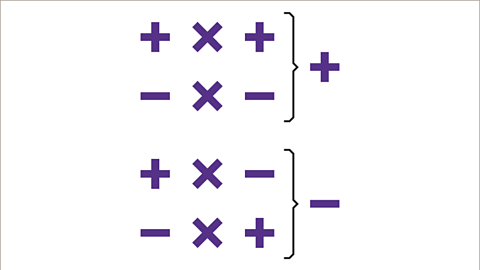
Image caption,
Start by completing the calculation using positive numbers first, then use the sign rules to find the sign of the answer.
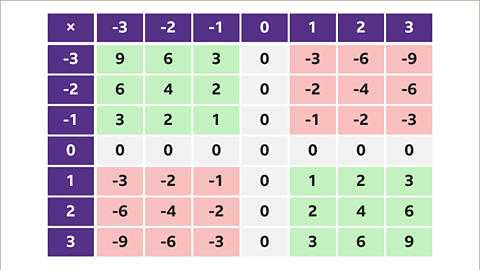
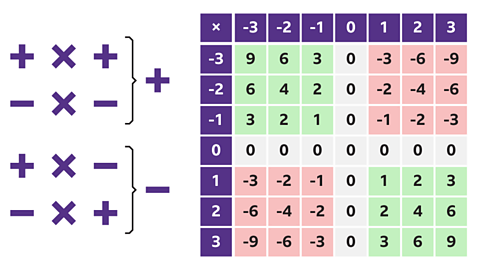
Image caption,
This multiplication table includes both positive and negative numbers. Follow the pattern to see the effect of multiplying by negative numbers.
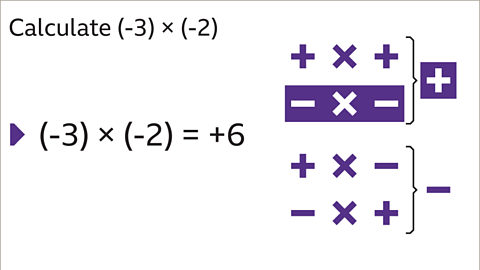
Image caption,
Calculate 3 × 2 initially to get 6, then remember that multiplying two numbers with the same sign means the answer will be positive, (-3) × (-2) = +6
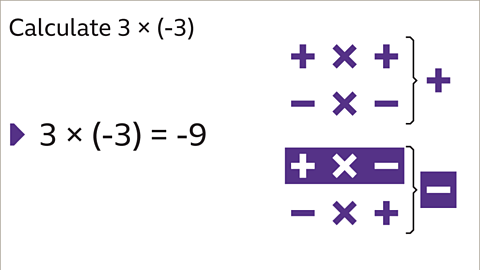
Image caption,
Calculate 3 × 3 initially to get 9, then remember that multiplying two numbers with different signs means the answer will be negative, 3 x (-3) = -9

When dividing negative numbers it is often useful to complete the calculation using positive numbers initially.Remember that:

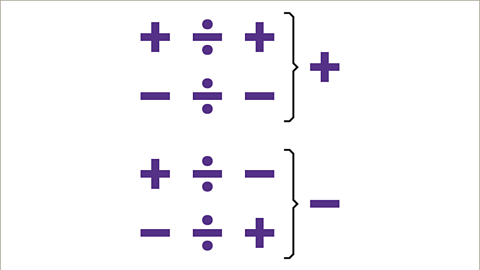
Image caption,
Start by completing the calculation using positive numbers first, then use the sign rules to find the sign of the answer.
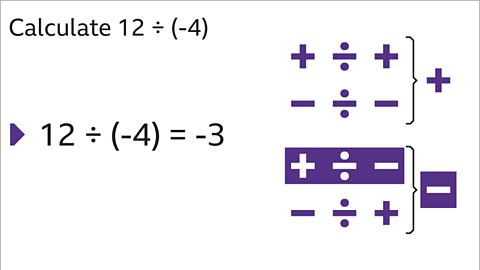
Image caption,
Calculate 12 ÷ 4 initially to get 3, then remember that dividing two numbers with different signs means the answer will be negative, 12 ÷ (-4) = -3
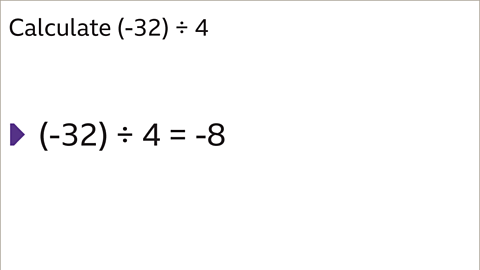
Image caption,
Calculate 32 ÷ 4 initially to get 8, then remember that dividing two numbers with different signs means the answer will be negative, (-32) ÷ 4 = -8

Calculate the following. You might need a pen and paper to note down the answers.

Remember that negative numbers are sometimes written in brackets. This can make the calculation easier to read.

Try this ordering activity to practise calculating with positive and negative numbers. You might need a pen and paper to help with your working out.

Practise multiplying and dividing positive and negative numbers in this quiz.

Negative numbers are used in everyday life, especially in business when making financial decisions and forecasting future profits.
Accountants and businesses use negative numbers to represent when money has already been or is going to be spent. Eg a regular outgoing of £300 per month on expenses is calculated as 12 x (-£300) over the next year.